4549
AMURA with standard single-shell acquisition can detect changes beyond the Diffusion Tensor: a migraine clinical study1Imaging Processing Laboratory, Universidad de Valladolid, Valladolid, Spain, 2Headache Unit, Hospital Clínico Universitario de Valladolid, Valladolid, Spain
Synopsis
AMURA (Apparent Measures Using Reduced Acquisitions) is an alternative formulation to drastically reduce the number of samples needed for the estimation of diffusion properties related to the Ensemble Average diffusion Propagator (EAP). Although these measures were initially intended for medium-to-high b-values, in this work we evaluate their performance in DTI-like acquisitions. Fifty healthy controls, 54 episodic migraine (EM) and 56 chronic migraine (CM) patients were compared, using a single-shell diffusion scheme at b=1000 s/mm2. We compare AMURA measures (return-to-origin, return-to-axis and return-to-plane probabilities) to traditional DTI measures. Differences between EM and controls were only detectable using the return-to-origin probability.
Introduction
In diffusion MRI (dMRI), the Ensemble Average diffusion Propagator (EAP) provides relevant microstructural information and meaningful descriptive maps of the white matter beyond the Diffusion Tensor (DT). In order to use the EAP in practical studies, scalar measures must be derived, being the most common the return-to-origin (RTOP), the return-to-plane (RTPP) and return-to-axis probabilities (RTAP). In order to drastically reduce the number of samples needed for the estimation of these measures, in 1 authors proposed a method so-called “Apparent Measures Using Reduced Acquisitions” (AMURA) that avoids the calculation of the whole EAP by assuming that the diffusion signal is roughly independent from the radial direction. Thus, closed form expressions for the measures were given.1–3 AMURA acquisitions remains compatible with single-shell acquisition, specially HARDI, where one single b-value is acquired. However, it has not been tested with lower b-values, more frequent in the clinical routine, in a whole-brain study.Our objective was to test whether AMURA measures calculated from a DT Imaging (DTI) compatible acquisition (single-shell and low b-value) could detect white matter alterations non-measurable using DTI scalar measures.
Methods
We acquired dMRI data from 50 Healthy Controls (HC), 54 Episodic Migraine (EM) and 56 Chronic Migraine (CM) patients, using the following parameters: TR = 9000 ms, TE = 86 ms, flip angle = 90º, 61 gradient directions, one baseline volume, b-value = 1000 s/mm2, 128 x 128 matrix size, 2 x 2 x 2 mm3 of spatial resolution and 66 axial slices covering the whole brain. Other details can be found elsewhere.4The diffusion-weighted images were preprocessed using MRtrix.5–8 DT was estimated using the “dtifit” tool from FSL. Fractional Anisotropy (FA), Mean (MD), Axial (AD) and Radial Diffusivity (RD) maps were obtained. RTOP, RTPP and RTAP were calculated using the AMURA tool.1–3
FA maps of every volume were warped to a common template with the standard tract-based spatial statistics (TBSS) pipeline.9 The same transformation was applied to MD, AD, RD, RTOP, RTPP and RTAP maps. Voxel-wise pairwise differences were assessed by the nonparametric permutation-based inference “randomise” tool.10 Five thousand permutations were set and results with p < 0.05 (family-wise error corrected) were considered as statistically significant. The minimum volume to consider significant results in a region was set to 30 mm3. Forty-eight regions from the JHU ICBM-DTI-81 White-Matter Labels Atlas were considered.11
Results
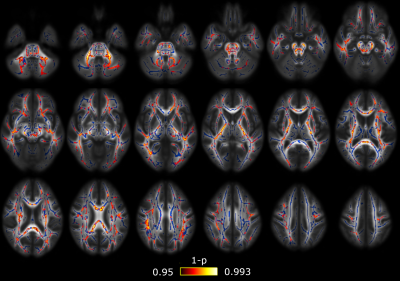
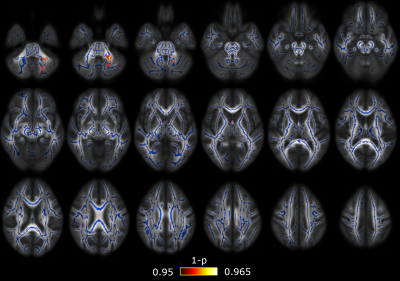
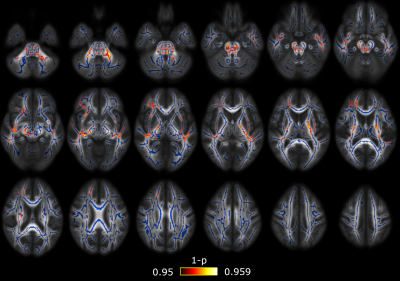
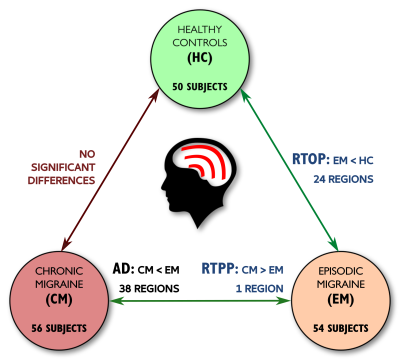
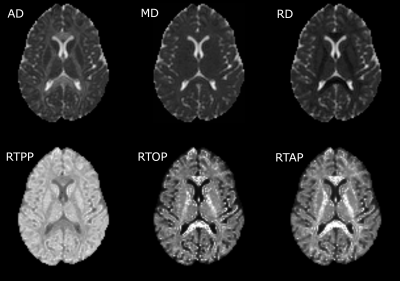
Significant differences between CM and EM were found for two measures: significant lower AD was found in CM compared to EM in 38 regions (Figure 1) and significant higher RTPP values were found in CM with respect to EM in one region (Figure 2). In the comparison between EM and HC, significant lower RTOP values were found in EM compared to HC in 24 regions (Figure 3). Finally, no significant differences were found in the comparison between CM and HC, or for FA, MD, RD or RTAP. All these results are summarized in Figure 4.Finally, for the sake of illustration, Figure 5 shows an axial slice of the DTI measures (MD, AD and RD) and AMURA (RTOP, RTPP and RTAP).
Discussion
AMURA measures can detect white matter alterations non-measurable with DTI using a single-shell approach with a low b-value, despite those measures were originally designed for large b-values. In addition to the possibility of the calculation of these metrics using just a single shell, AMURA requires much less processing time with respect to those methods that need to estimate the whole EAP.1 Hence, AMURA can be a robust complement for DTI studies.In this study, only with AMURA were we able to find differences between healthy controls and episodic migraine patients: only the RTOP could detect these differences. This result reflects the usefulness of AMURA to characterize white matter properties, even with low b-values. Even using dMRI acquisition parameters typical in the clinical routine, white matter alterations non-measurable with DTI can be found with AMURA. In line with our results, in comparison to MD, RTOP has been described as a better descriptor of cellularity and restricted diffusion.12
In the case of RTPP, we found significant higher values in CM compared to EM, while lower AD values in CM compared to EM were found. Since RTPP is related to the main diffusion direction, results are consistent. In this case, the use of a low b-value produces a suboptimal RTPP estimation that gives a much lower number of regions with significant differences in comparison to AD.
Finally, note that if a Gaussian EAP is assumed, the three measures can also be computed as a function of the inverse of the eigenvalues of the DT.1 We have also tried this implementation for the study proposed in this work. However, the fact that RTOP and RTAP depend on the smallest eigenvalue produces a great number of outliers in the areas with higher anisotropy that makes the clinical analysis unfeasible. Consequently, although RTOP, RTAP and RTPP could also have been implemented using a DT, we have discarded that approach in favor of AMURA, which produces more robust results.
Conclusion
AMURA can detect white matter alterations complementary to DTI using dMRI acquisition parameters from clinical routine (single-shell and low b-value).Acknowledgements
This work has been supported by Ministerio de Ciencia
e Innovación of Spain with research grant RTI2018-094569-B-I00. ÁPG
was supported by Junta de Castilla y León (Spain) and the European Social Fund
(ID: 376062, Base de Datos Nacional de Subvenciones).
References
1. Aja-Fernández S, de Luis-García R, Afzali M, Molendowska M, Pieciak T, Tristán-Vega A. Microstructure Diffusion Scalar Measures from Reduced MRI Acquisitions. bioRxiv. 2019. https://www.biorxiv.org/content/10.1101/772897v1 (accessed 2 November 2019).
2. Aja-Fernández S, Tristán-Vega A, Molendowska M, Pieciak T, de Luis-García R. Return-to-the-origin probability calculation in single shell acquisitions. In: International Society of Magnetic Resonance in Medicine 26th Annual Meeting and Exhibition. Paris, France; 2018:1414.
3. Aja-Fernández S, Tristán-Vega A, Molendowska M, Pieciak T, de Luis-García R. Return-to-Axis Probability Calculation from Single-Shell Acquisitions. In: Medical Image Computing and Computer Assisted Interventions Conference (MICCAI): Computational Diffusion MRI. Springer; 2019:29-41.
4. Planchuelo-Gómez Á, García-Azorín D, Guerrero ÁL, Aja-Fernández S, Rodríguez M, de Luis-García R. Structural connectivity alterations in chronic and episodic migraine: A diffusion magnetic resonance imaging connectomics study. Cephalalgia. [journal on the Internet]. 2019 [cited 2019 Nov 6]. doi:10.1177/0333102419885392. [Epub ahead of print].
5. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage. 2016;142:394-406.
6. Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage. 2015;125:1063-1078.
7. Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20:45-57.
8. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:S208-S219.
9. Smith SM, Jenkinson M, Johansen-Berg H, et al. Tract-based Spatial Statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31(4):1487-1505.
10. Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp. 2002;15(1):1-25.
11. Mori S, Wakana S, Nagae-Poetscher LM, van Zijl PC. MRI Atlas of Human White Matter. Amsterdam: Elsevier; 2005.
12. Avram A V, Sarlls JE, Barnett AS, et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. Neuroimage. 2016;127:422-434.
Figures