4541
A novel diffusion registration method with the NTU-DSI-122 template to transform free water signal fraction maps to stereotaxic space.1Department of Radiology & Medical Imaging, Division of Neuroradiology, University of Virginia Health System, University of Virginia, Charlottesville, VA, United States, 2Brain Institute, University of Virginia, Charlottesville, VA, United States
Synopsis
We propose the use of the NTU-DSI-122 template as a flexible, diffusion specific, means of registering subject images to stereotaxic MNI-space for further analysis. This allows for registration to be performed based on matching white matter fiber orientation distributions, which create within tissue contrasts, unlike voxel intensity metrics. This advantage is demonstrated by observing the increased consistency of registration versus a leading intensity-based algorithm. The range of b-values present in the NTU-DSI-122 allows for tailoring to selectively register at b-values matching those acquired in an experimental cohort, providing flexibility for both single- and multi-shell acquisitions.
Introduction
Registering subjects to a common template space is a necessary step in almost any neuroimaging study. A straightforward process for doing so aligns the brains of each acquisition in a study cohort from the acquired ‘native’ space to a ‘common’ template space. This common space is intended to achieve voxel-voxel correspondence between images and allow for comparison between subjects without interference from factors such as head orientation in the scanner or naturally occurring anatomical variation. The idea of a stereotaxic common space that could allow for images, atlases, and ROIs from different studies to be applied in a standardized manner gained attention with the definition of Talairach space-registered atlases1, and the release of stereotaxic templates such as the Colin 27 Average Brain2, and the MNI 152 linear template3.Aligning subject brains in native space to these templates in stereotaxic space is frequently performed using intensity-based registration, which attempts to minimize voxel-voxel differences between native and template images. One of the most widely applied registration algorithms in neuroimaging, the ‘SyN’ model implemented in the program ANTs4, utilizes a diffeomorphic regularization to minimize the intensity difference between images (by maximizing a cross-correlation metric), combined with assistance from anatomical priors5. This has been demonstrated to be a highly reproducible brain image registration method5, and has performed well against other methods in open competitions6,7.
Diffusion MRI registration can be challenging due to large changes in voxel intensity between b-value shells, and different contrast at each b-value shell depending on the tissue within the voxel8. One solution to this problem has been to register the b=0 volumes collected with the diffusion images to a T2-weighted image9-11 due to the similar anatomical contrast present in both images. The voxel-wise image intensity between two white matter (WM) fiber bundles may not be greatly different at b=0 (i.e., they lack within tissue contrast), thus intensity-based algorithms may have lower sensitivity toward within tissue location. However, the orientation of those WM fiber bundles is important for tractography and reconstructing accurate connectomes. Additionally, some measures of cellular microstructure, such as free water signal fractions, have a small value range (between 0-1 in this case), making the measure sensitive to even small changes in value or introduction of noise. Symmetric diffeomorphic registration via cross-correlation of the spherical hormonic coefficients has previously been demonstrated as a means of accurately co-registering WM fiber orientation distributions (FODs) within a cohort12 but not to stereotaxic space.
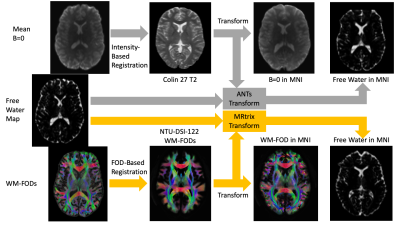
The NTU-DSI-122 template is a composite template composed of 122 individual subjects registered in stereotaxic MNI space13. Rather than a single volume, the template consists of 102 individual gradient directions and 12 different b-value shells. By extracting the b-value shells corresponding to collected experimental data, then calculating the FOD using constrained spherical deconvolution14,15, it is possible to generate an FOD-based template for registering diffusion data in stereotaxic space. In this study we demonstrate that FOD-based registration from an experimental cohort leads to more consistent transforms of free water signal fraction maps compared to intensity-based registration.
Methods
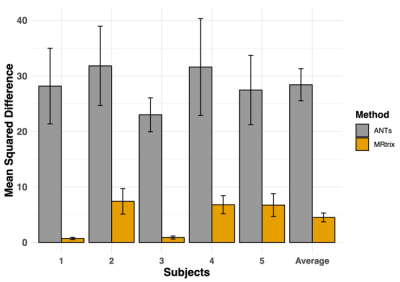
We collected 5 diffusion MRIs from healthy controls using a Siemens Prisma 3T scanner with an isotropic voxel size of 1.7⨉1.7⨉1.7mm3, TE=70ms and TR=2900ms; 10 b=0 images and 64 gradient directions at both b=1500s/mm2 and b=3000s/mm2. Each image set was analyzed using MSMT-CSD14 implemented in the open source software MRtrix16. Several preprocessing steps utilized FSL17. Diffusion images were denoised18, corrected for Gibbs ringing19, susceptibility distortions20, motion21, and eddy currents22. Response functions were generated23 from both experimental data and the NTU-DSI-122 template at b=1538s/mm2 and b=3077s/mm2 and used to generate FODs14. The number of directions was sufficient to generate FODs with a harmonic order of lmax = 4, which has been suggested to be optimal for registration12. CSF-like signal fractions were calculated from the FODs24,25.Each of the 5 diffusion MRIs were then registered from native space to MNI space using both ANTs SyN algorithm4 to register the processed b=0 images with the Colin 272 T2 template and using MRtrix16 to register the WM FODs with the NTI-DSI-122 template WM FODs12,26. Each registration was used to generate a transform that was applied to the CSF-like free water signal fraction from that subject. Because these registrations are not deterministic processes, and can produce slightly different transforms each time it is performed on the same images, this procedure was repeated independently 5 times for each subject, via each method (Figure 1). The mean squared difference was then calculated for each whole-brain image between every same-method same-subject combination to analyze which method more consistently transformed the free water signal fraction map into MNI space.
Results
The MRtrix FOD transform resulted in a significantly lower mean squared difference between repetitions compared to the ANTs SyN generated transform (pairwise T-test, T49 = 8.02, p<0.001) indicating that the FOD algorithm was able to more consistently register and transform the free water signal fraction maps (Figure 2).Conclusion
This study demonstrates the ability of the NSU-DSI-122 template to serve as a useful means to register experimentally collected diffusion data and free water signal fraction maps in stereotaxic space. The use of FOD-based registration reduces variation between registration attempts, minimizing the introduction of noise.Acknowledgements
No acknowledgement found.References
1. Collins, D. L., Neelin, P., Peters, T. M., & Evans, A. C. (1994). Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. Journal of computer assisted tomography, 18(2), 192-205.
2. Fonov, V., Evans, A. C., Botteron, K., Almli, C. R., McKinstry, R. C., Collins, D. L., & Brain Development Cooperative Group. (2011). Unbiased average age-appropriate atlases for pediatric studies. Neuroimage, 54(1), 313-327.
3. Holmes, C. J., Hoge, R., Collins, L., Woods, R., Toga, A. W., & Evans, A. C. (1998). Enhancement of MR images using registration for signal averaging. Journal of computer assisted tomography, 22(2), 324-333.
4. Avants, B. B., Tustison, N. J., Stauffer, M., Song, G., Wu, B., & Gee, J. C. (2014). The Insight ToolKit image registration framework. Frontiers in Neuroinformatics, 8, 44.
5. Avants, B. B., Tustison, N. J., Song, G., Cook, P. A., Klein, A., & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage, 54(3), 2033-2044.
6. Klein, A., Andersson, J., Ardekani, B. A., Ashburner, J., Avants, B., Chiang, M. C., ... & Song, J. H. (2009). Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage, 46(3), 786-802.
7. Fu, Z., Lin, L., Tian, M., Wang, J., Zhang, B., Chu, P., ... & Wu, S. (2017). Evaluation of five diffeomorphic image registration algorithms for mouse brain magnetic resonance microscopy. Journal of microscopy, 268(2), 141-154.
8. Jeurissen, B., Tournier, J. D., Dhollander, T., Connelly, A., & Sijbers, J. (2014). Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411-426.
9. Huang, H., Ceritoglu, C., Li, X., Qiu, A., Miller, M. I., van Zijl, P. C., & Mori, S. (2008). Correction of B0 susceptibility induced distortion in diffusion-weighted images using large-deformation diffeomorphic metric mapping. Magnetic resonance imaging, 26(9), 1294-1302.
10. McLaughlin, N. C., Paul, R. H., Grieve, S. M., Williams, L. M., Laidlaw, D., DiCarlo, M., ... & Gordon, E. (2007). Diffusion tensor imaging of the corpus callosum: a cross-sectional study across the lifespan. International journal of developmental neuroscience, 25(4), 215-221.
11. Pierpaoli, C., Walker, L., Irfanoglu, M. O., Barnett, A., Basser, P., Chang, L. C., ... & Wu, M. (2010). TORTOISE: an integrated software package for processing of diffusion MRI data. In 18th Scientific Meeting of the International Society for Magnetic Resonance in Medicine (p. 1597).
12. Raffelt, D., Tournier, J. D., Fripp, J., Crozier, S., Connelly, A., & Salvado, O. (2011). Symmetric diffeomorphic registration of fibre orientation distributions. NeuroImage, 56(3), 1171-1180.
13. Hsu, Y. C., Lo, Y. C., Chen, Y. J., Wedeen, V. J., & Isaac Tseng, W. Y. (2015). NTU‐DSI‐122: A diffusion spectrum imaging template with high anatomical matching to the ICBM‐152 space. Human brain mapping, 36(9), 3528-3541.
14. Jeurissen, B., Tournier, J. D., Dhollander, T., Connelly, A., & Sijbers, J. (2014). Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411-426.
15. Dhollander, T., & Connelly, A. (2016). A novel iterative approach to reap the benefits of multi-tissue CSD from just single-shell (+ b=0) diffusion MRI data. In Proc ISMRM (Vol. 24, p. 3010).
16. Tournier, J. D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T., Pietsch, M., ... & Connelly, A. (2019). MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage, 116137.
17. Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782-790.
18. Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic resonance in medicine, 76(5),1582-1593.
19. Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magnetic resonance in medicine, 76(5), 1574-1581.
20. Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F., Behrens, T. E., Johansen-Berg, H., ... & Niazy, R. K. (2004). Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage, 23, S208-S219.
21. Andersson, J. L., Graham, M. S., Zsoldos, E., & Sotiropoulos, S. N. (2016). Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage, 141, 556-572.
22. Andersson, J. L., & Sotiropoulos, S. N. (2016). An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 125, 1063-1078
23. Dhollander, T., Raffelt, D., & Connelly, A. (2016). Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image. In ISMRM Workshop on Breaking the Barriers of Diffusion MRI(Vol. 5).
24. Newman, B. T., Dhollander, T., Reynier, K. A., Panzer, M. B., & Druzgal, T. J. (2019). Test-retest reliability and long-term stability of 3-tissue constrained spherical deconvolution methods for analyzing diffusion MRI data. bioRxiv, 764506.
25. Mito, R., Dhollander, T., Xia, Y., Raffelt, D., Salvado, O., Churilov, L., ... & Connelly, A. (2019). In vivo microstructural heterogeneity of white matter lesions in Alzheimer's disease using tissue compositional analysis of diffusion MRI data. bioRxiv, 623124.
26. Raffelt, D., Tournier, J. D., Crozier, S., Connelly, A., & Salvado, O. (2012). Reorientation of fiber orientation distributions using apodized point spread functions. Magnetic Resonance in Medicine, 67(3), 844-855.
Figures