4517
Quantification of uncertainty in parameterisations of cardiac myofibre orientations from diffusion-weighted imaging
Bianca Freytag1, Vicky Y Wang2, Alistair A Young3, and Martyn P Nash1
1Auckland Bioengineering Institute, The University of Auckland, Auckland, New Zealand, 2Veterans Affairs Medical Center, San Francisco, CA, United States, 3Biomedical Engineering Department, King's College London, London, United Kingdom
1Auckland Bioengineering Institute, The University of Auckland, Auckland, New Zealand, 2Veterans Affairs Medical Center, San Francisco, CA, United States, 3Biomedical Engineering Department, King's College London, London, United Kingdom
Synopsis
Electro-mechanical models of heart function rely upon accurate representation of microstructural orientations in the myocardium. We assessed the sensitivity of a finite element parameterisation of the myofibre orientation field derived from high-resolution DWI data of a canine heart. Eigenanalysis of the indifference region in the neighbourhood of the optimal fit of the myofibre field enabled quantification of helix angle uncertainty consistent with the DWI data. This method can be used to propagate the uncertainty in myofibre parameterisation to electro-mechanics simulation results.
Introduction
Electro-mechanical models of heart function rely upon accurate representation of microstructural orientations in the myocardium1-3. In particular, a continuous helix angle field, defining myocyte orientation over the entire heart, is a vital input for electro-mechanical simulations. The construction of personalised cardiac models can be subject to several types of uncertainty: 1) measurement accuracy; 2) inability of diffusion-weighted imaging (DWI) to capture exact microstructural orientations; 3) error in parameterisations of microstructural orientation fields; and 4) error in geometric models fitted to experimental data. The uncertainty in data or models affects parameter identifiability, such that multiple solutions with an equal goodness-of-fit may be found4. In other words, error in fitting microstructural orientation fields to DWI data is propagated to simulations, which use the fitted myofibre fields to prescribe the axes of anisotropic mechanical response. To investigate the impact that variations in microstructural orientations have on cardiac modelling, the uncertainty in the parameterisations needs to be quantified.In this study, we computed an indifference region for myofibre orientation fields that were parameterised from high-resolution DWI. Parameters that lie within this indifference region yield equally acceptable goodness-of-fit of the field to the DWI data.
Methods
Microstructural orientation field fitting and subsequent uncertainty analyses were performed on a DWI dataset of an ex-vivo canine heart provided by researchers from the Johns Hopkins University5. The study was approved by the local Institutional Review Boards and conformed to the NIH Guide for the Care and Use of Laboratory Animals. The image resolution was 780 µm x 780 µm x 900 µm (128 voxel x 128 voxel).To parameterise the microstructural data using a finite element (FE) model, we fitted the endocardial and epicardial surfaces of a regular shaped prolate spheroid (16-element tricubic Hermite) model to the corresponding surfaces segmented from the DWI data6.
Myofibre orientation field fitting was performed according to previously described methods7. In brief, Euler angles were defined at each of the 34 FE nodes and interpolated linearly over the model. The helix angles were interpolated at each voxel and used to construct a myofibre orientation vector $$$(\mathbf{f})$$$ to evaluate the objective function $$$(\Psi)$$$ that optimises the alignment of $$$\mathbf{f}$$$ with the strongest direction of diffusion, as quantified using the diffusion tensor.
After the optimal helix angle field parameters $$$(\hat{\boldsymbol{\theta}})$$$ fitted to the DWI data were found, a 34 x 34 entry Hessian matrix $$$(\mathbf{H}_{\hat{\boldsymbol{\theta}}})$$$ at the optimum was estimated numerically using central differences.
Hence, the indifference region can be based on contours of $$$\Psi(\boldsymbol{\theta})$$$ given by $$$\Psi(\boldsymbol{\theta})=\Psi_{\hat{\boldsymbol{\theta}}}+\Delta$$$, where $$$\Delta$$$ is the offset value added to the optimal objective function value $$$(\Psi_{\hat{\boldsymbol{\theta}}})$$$. From a second-order Taylor series expansion of the objective function, we obtain:$$ (\boldsymbol{\theta} - \hat{\boldsymbol{\theta}})^T\boldsymbol{H}_{\hat{\boldsymbol{\theta}}}(\boldsymbol{\theta}-\boldsymbol{\hat\theta})=2\times\Delta.$$We use this offset value to scale the Hessian at the optimal set of parameters:$$\tilde{\boldsymbol{H}}_{\hat{\boldsymbol{\theta}}}=\frac{\boldsymbol{H}_{\hat{\boldsymbol{\theta}}}}{2\times\Delta}.$$The inverse of the scaled Hessian $$$(\boldsymbol{C}_{\hat{\boldsymbol{\theta}}} = \tilde{\boldsymbol{H}}_{\hat{\boldsymbol{\theta}}}^{-1})$$$ is decomposed using eigenanalysis. The eigenvectors $$$(\boldsymbol{e}_i)$$$ and eigenvalues $$$(\lambda_i)$$$ of $$$\boldsymbol{C}_{\hat{\boldsymbol{\theta}}}$$$ represent the principal axes of indifference of the objective function (fitting error). A parameter set $$$(\boldsymbol{\theta}_i)$$$ along the $$$i^{th}$$$ principal axis, defined by $$$\boldsymbol{e}_i$$$, corresponds to an objective function value at the indifference level when$$\boldsymbol{\theta}_i=\hat{\boldsymbol{\theta}}\pm\boldsymbol{e}_i\times\sqrt{\lambda_i}.$$The optimal helix angle field can be associated with fields of perturbed parameters away from that optimum, defined by the indifference region. The primary eigenvector of $$$\boldsymbol{C}_{\hat{\boldsymbol{\theta}}}$$$ describes the direction of greatest uncertainty of the parameters, and the primary eigenvalue describes how much the optimal field can be perturbed along this direction before the objective function changes by more than $$$\Delta$$$. Here, $$$\Delta$$$ was chosen so that the average difference in helix angles between the optimal field and the perturbed field, interpolated at each voxel, was between 7° - 8° (to match the commonly observed accuracy in myofibre orientation quantification from DWI8). Figure 1 illustrates the workflow to assess these perturbations.
Results
Figure 2 presents some exemplary perturbations of the optimal helix angle field. The direction of greatest parameter uncertainty exhibited a chequerboard pattern, and the most sensitive mode induced an almost homogeneous offset of nodal helix angles.Discussion and Conclusions
In this study, the intra-subject uncertainty of helix angle fields with respect to DWI data was quantified.The analysis led to a number of interesting observations. For the least sensitive perturbation, a chequerboard pattern emerges (blue-to-green illustration, Figure 2). It appears that, if the helix angle is increased at one node, this increase is counterbalanced at adjacent nodes in the mesh. This was observed circumferentially, longitudinally and radially. The most sensitive perturbation is substantially different such that it is an almost constant offset in helix angles for all nodes. The magnitudes of the nodal helix angle differences were much smaller for the most sensitive perturbation since that was the direction along which the parameters were most well-defined. On the other hand, the greatest uncertainty in nodal helix angle parameters was associated with the perturbation direction along which the objective function was least sensitive to the parameter changes (i.e. the primary eigenvector of the indifference region).
This framework to estimate the uncertainty in helix angle field parameters is a starting point to further the understanding of the effects that uncertainty in microstructural orientation fields has on biophysical predictions using subject-specific cardiac modelling and simulation.
Acknowledgements
We thank Daniel B. Ennis of Stanford University for providing the DWI data. We gratefully acknowledge the financial support from the Health Research Council of New Zealand (17/608).References
- L. K. Waldman, D. Nosan, F. Villarreal, and J. W. Covell, “Relation between transmural deformation and local myofiber direction in canine left ventricle.,” Circulation Research, vol. 63, no. 3, pp. 550–562, 1988
- K. D. Costa, Y. Takayama, A. D. McCulloch, and J. W. Covell, “Laminar fiber architecture and three-dimensional systolic mechanics in canine ventricular myocardium,” American Journal of Physiology - Heart and Circulatory Physiology, vol. 276, no. 2, pp. H595–H607, 1999
- K. D. Costa, J. W. Holmes, and A. D. McCulloch, “Modelling cardiac mechanical properties in three dimensions,” Philosophical Transactions of the Royal Society of London, vol. 359, no. 1783, pp. 1233–1250, 2001
- D. Neumann, T. Mansi, B. Georgescu, A. Kamen, E. Kayvanpour, A. Amr, F. Sedaghat-Hamedani, J. Haas, H. Katus, B. Meder, J. Hornegger, and D. Comaniciu, “Robust Image-Based Estimation of Cardiac Tissue Parameters and Their Uncertainty from Noisy Data,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2014 (P. Golland, N. Hata, C. Barillot, J. Hornegger, and R. Howe, eds.), vol. 8674, pp. 9–16, Cham: Springer International Publishing, 2014
- D. B. Ennis, Assessment of Myocardial Structure and Function Using Magnetic Resonance Imaging. PhD thesis, John Hopkins University, 2004
- V. Y. Wang, H. I. Lam, D. B. Ennis. B. R. Cowan, A. A. Young, M. P. Nash. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Medical Image Analysis, vol. 13, no 5, pp. 773–784, 2009
- B. Freytag, V. Y. Wang, G. R. Christie, A. J. Wilson, G. B. Sands, I. J. LeGrice, A. A. Young, and M. P. Nash, “Field-Based Parameterisation of Cardiac Muscle Structure from Diffusion Tensors,” in Functional Imaging and Modeling of the Heart 2015, Lecture Notes in Computer Science 9126 (H. van Assen, P. Bovendeerd, and T. Delhaas, eds.), pp. 146–154, 2015
- L. Geerts, R. Kerckhoffs, P. Bovendeerd, and T. Arts, “Towards Patient-Specific Models of Cardiac Mechanics: A Sensitivity Study,” in Functional Imaging and Modeling of the Heart (G. Goos, J. Hartmanis, J. van Leeuwen, I. E. Magnin, J. Montagnat, P. Clarysse, J. Nenonen, and T. Katila, eds.), vol. 2674, pp. 81–90, Springer Berlin Heidelberg, 2003.
Figures
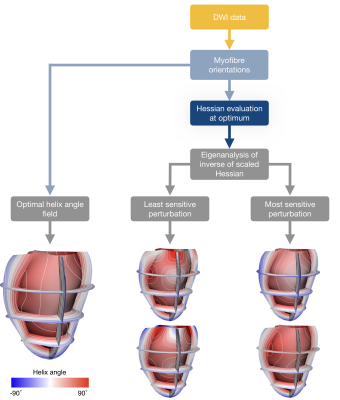
Overview of the workflow to compute the perturbations corresponding to the variation in helix angle parameters from DWI data.
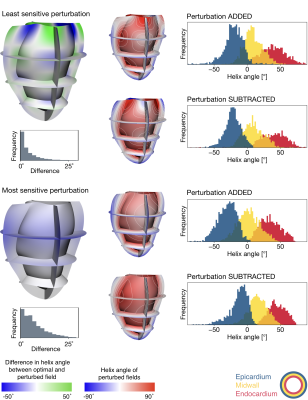
Perturbations in helix angle fields at the border of the objective function’s indifference region, alongside histograms of endocardial, midwall, and epicardial helix angles (separated into transmural thirds). Blue-to-green colour maps illustrate the perturbations associated with the smallest (top panel) and greatest (bottom panel) magnitudes of indifference. The distributions of helix angle differences derived from optimal and perturbed fields are shown in grey histograms. Each perturbation was added or subtracted from the optimal field to create the blue-to-red fields.