4508
Validating pore size estimates in a biomimetic microfibre architecture with a stochastic distribution of pore-sizes and cross-sectional shapes1Department of Biomedical Imaging and Radiological Science, National Yang Ming University, Taipei, Taiwan, 2Institute of Science and Technology for Brain Inspired Intelligence, Fudan University, Shanghai, China, 3Aging and Health Research Center, National Yang-Ming University, Taipei, Taiwan, 4Cardiff University Brain Research Imaging Center (CUBRIC), Cardiff University, Cardiff, United Kingdom, 5Centre for Medical Image Computing, University College London, London, United Kingdom, 6Institute of Neuroscience, National Yang-Ming University, Taipei, Taiwan
Synopsis
Previous studies showed that AxCaliber-like frameworks produce reliable orientation and inner diameter estimates in idealised phantoms (i.e., highly parallel hollow cylinders with uniform circular cross-section). We extend this work to ‘biomimetic’ phantoms, having stochastic pore-size distributions, non-circular cross sections and complex (i.e., crossing) fibre configurations. Using a Connectom scanner, and assuming a Poisson pore-size distribution, inner diameter and crossing angle estimates were in excellent agreement with electron-microscopy measurements in the same sample. To our knowledge, this is the first validation of pore-size estimates in complex geometries on a human scanner, lending support to the promise of mapping these parameters in-vivo.
Introduction
The capability of diffusion magnetic resonance imaging (dMRI) to quantify microstructure has recently drawn attention over the last decade due to the advance in gradient power in the MRI scanner1. Recently, remarkable progress on quantifying the axonal fraction and compartment size has been achieved2. However, validation in phantoms has been limited to parallel fibre bundles with circular cross-section and uniform diameter. It is still unclear, however, whether dMRI can reliably estimate the microstructure of tissue with complex architecture including crossing fibre bundles and a distribution of diameters with non-uniform cross-sectional shaper. In this study, we validate the quantitative estimates in dMRI using a new biomimetic phantom3 that has a stochastic distribution of diameters and multiple fibre orientations, which are the desirable properties to approximate some of the complex properties of white matter microstructure found in the human brain.Methods
A single-blind experiment was conducted in order to perform the scans and analyses objectively. In other words, the researchers performing the MRI analyses did not know anything about the specification of the phantoms until reporting the results back to the manufacturer. The imaging experiments were performed on a Siemens 3T Connectom scanner which comprised CHARMED4 and 3D-AxCaliber scans5,6. The CHARMED data were acquired at Δ = 24ms, δ = 7ms, at 6 b-values (200, 500, 1200, 2400, 4000, 6000 s/mm2) in non-collinear directions (20, 20, 30, 61, 61, 61 respectively). The AxCaliber scans were performed with Δ = 18, 27, 36, 45, 60, 90 ms with δ = 7ms, at scaled b-values [2200 to 25500 s/mm2] with corresponding gradient strength around 200 and 288 mT/m in 30 non-collinear directions. The total scan time was 54 minutes, matches the scanning protocol used locally for human brain. The preprocessed CHARMED data with a b-value of 2400 s/mm2 were extracted and used to identify the number of distinct fibre populations in each voxel of the image using spherical harmonics deconvolution (CSD)7,8. Based on the estimated number of fiber populations, the CHARMED model was utilized to estimate the major fibre directions as the prior fixed parameters to provide the initial starting point of restricted diffusion signal fractions. Finally, the cascaded AxCaliber model with a continuous Poisson distribution9 was used to calculate the diameter distribution on each voxel via the Microstructure Diffusion Toolbox10.Results
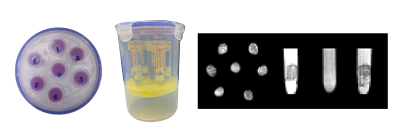
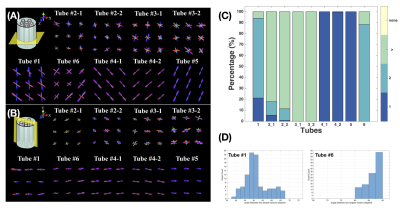
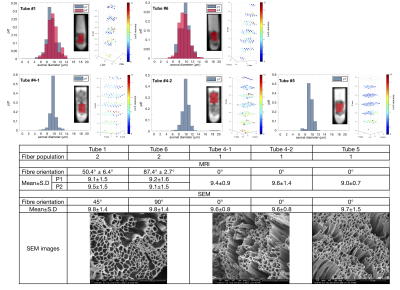
Figure 1 shows the overview of the phantom that contains nine samples in six tubes. Figure 2A and 2B shows the estimated number of unique fibre orientations via CSD. As the number of unique populations in Tubes 2 and 3 was much larger than 3, due to dimensionality explosion, the AxCaliber model was not fitted to these tubes. Thus only five samples were examined. In these five samples, three samples (Tube 4-1, 4-2, and 5) showed a single fibre population, while two samples with crossing fibre populations were observed in Tube 1 (50.4° ± 6.43°) and Tube 6 (87.4° ± 2.72°), the estimated distribution of crossing angle within each voxel is shown in Figure 2C. Figure 3 shows the histograms and 3D plots of the mean fibre diameter in each voxel of the different samples. The estimated average inner diameters of the fibres were similar across samples, around 9 μm, which is highly consistent with the estimated values derived from SEM (see Figure 3).Discussion and Conclusions
In summary, by spanning multiple diffusion times and gradient strengths on an ultra-strong gradient scanner, we successfully estimated the fibre diameters that had an expected diameter under 10 μm in both single-aligned and cross-orientated fibres on a new biomimetic phantom with non-uniform cross-sections, that more closely mimics white matter than previously-employed simple geometric phantoms. Our work demonstrated the strength and reliability of 3D-AxCaliber model to resolve the complex fibre architectures in this type of phantom. Future work is underway to validate pore-size estimates in phantoms with 3 or more crossing populations (including completely random), and smaller pore-sizes than studied here. We caution against full extrapolation to ‘axon diameter’ mapping. The phantom does contain some ‘extra-axonal’-like pores, due to the stochastic nature of the manufacturing process, but this does not yet fully license claims about validating axon diameter in vivo. Nevertheless, this study can be considered a useful evolution in the process of validating pore size in complex more biomimetic geometries on a human scanner.Acknowledgements
This study was supported in part by grants from Ministry of Science and Technology, Taiwan (MOST 108-2321-B-010-010-MY2)References
1. Huang SY, Nummenmaa A, Witzel T, Duval T, Cohen-Adad J, Wald LL, et al. The impact of gradient strength on in vivo diffusion MRI estimates of axon diameter. Neuroimage. 2015;106:464-472.
2. Fan Q, Nummenmaa A, Wichtmann B, Witzel T, Mekkaoui C, Schneider W, et al. Validation of diffusion MRI estimates of compartment size and volume fraction in a biomimetic brain phantom using a human MRI scanner with 300mT/m maximum gradient strength. Neuroimage. 2018;182:469-478.
3. Zhou FL, Li Z, Gough JE, Hubbard Cristinacce PL, Parker GJM. Axon mimicking hydrophilic hollow polycaprolactone microfibres for diffusion magnetic resonance imaging. Mater Des. 2018; 137:394-403.
4. Assaf, Y., Basser, PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. NeuroImage. 2005;27:48–58.
5. Barazany D, Jones DK, Assaf Y. AxCaliber 3D. In: Proc ISMRM 19th Annual Meeting, Montreal, Canada. 2011;
6. Assaf, Yaniv, Tamar Blumenfeld Katzir, Yossi Yovel, and Peter J Basser. “Axcaliber: a Method for Measuring Axon Diameter Distribution From Diffusion MRI.” Magnetic Resonance in Medicine. 2008; 59(6):1347–54.
7. Jeurissen B, Leemans A, Tournier JD, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp. 2013;34:2747-2766.
8. Tournier JD, Yeh CH, Calamante F, Cho KH, Connelly A, Lin CP. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage. 2008;42:617-625.
9. de Santis S, Jones DK, Roebroeck A. Including Diffusion Time Dependence in the Extra-Axonal Space Improves in Vivo Estimates of Axonal Diameter and Density in Human White Matter. NeuroImage. 2016;130: 91–103.
10. Harms, R L, F J Fritz, A Tobisch, R Goebel, A Roebroeck. Robust and Fast Nonlinear Optimization of Diffusion MRI Microstructure Models. NeuroImage. 2017;155: 82–96.
Figures