INTRODUCTION

New approaches and models have been developed to obtain the microstructure of spinal cord by dMRI.¹ However, there has been no dedicated phantoms that can be used to validate diffusion MR measurements in spinal cord. We have previously developed tissue-mimicking MR phantoms from co-electrospun hollow microfibres.^2-4 Here we demonstrate a spinal cord phantom constructed from hollow microfibres and assesses its potential as a tool for validating MR measurement on a 3T clinical scanner.

METHODS

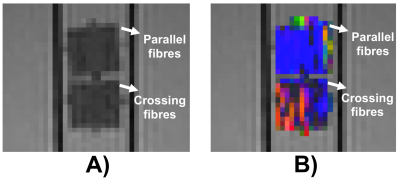
Microstructural characterisation and phantom construction
A ~0.5 mm thickness microfibre strip was fabricated by co-electrospinning, as previously described.⁵ Pore diameter was calculated from 5 SEM images for each sample using ImageJ.⁶ Two phantom samples were constructed by packing two blocks of 24 fibre layers (10 mm×10 mm) into a 15 ml centrifuge tube filled with water having approximate diameter of spinal cord (1-12 µm).⁷ Fibres in one block were uniaxially aligned (0^o) and in the other were interleaved, crossed at 90^o. The two samples assembled into a cylindrical plastic container (inner diameter: ~140 mm; height: ~180 mm) that can house up to 7 samples.

MR acquisition and analysis
The phantom filled with water was scanned on a 3T Philips Ingenia CX with the vendor’s 64-channel head coil to characterise its diffusion and relaxation properties. The MRI protocol included: 3D T2-weighted turbo spin echo for anatomical localisation (resolution: 1 mm isotropic; TR: 2200 ms; TSE factor: 90; TSE echo spacing: 4.7 ms; TE equivalent: 110 ms; compressed-SENSE factor of 7); 3D spoiled gradient echo (SPGR) imaging for T1, T2* and proton density (PD) mapping (resolution: 1 mm isotropic; TR: 28.5 ms; TE/echo spacing = 2.3/3.3 ms for 6 echoes; flip angles: 4° and 24°; compressed-SENSE factor of 6) and for B1 mapping (actual flip angle imaging; resolution: 4 mm isotropic; TR1/TR2: 30/180 ms/ms; TE: 2.1 ms); ZOOM-EPI DW imaging (reduced-field-of-view of 64x48 mm²; resolution: 1x1 mm²; 12 3-mm thick slices acquired in 3 packages; TR = 6000 ms; 1 b = 0 at each of TE = {20, 30, 60, 64, 90, 120, 200} ms and 24 directions at each of b = {1200, 2500} s/mm² with TE = 64 ms). Scans were performed at room temperature (T = 23.3°C with intrinsic water self-diffusivity estimated to be 2.2 mm² ms^–1).

From two SPGR scans with minimum TE and different flip angles we derived quantitative T1,⁸ correcting nominal flip angles with B1 map. Multiple SPGR echoes acquired at a flip angle of 24° were instead used to calculate T2*. Relaxometry metrics enabled the calculation of quantitative PD with the method of pseudo proton densities,⁹ taking care of normalising phantom’s PD to that of surrounding water. Then, diffusion data were analysed by fitting DTI model to the lowest b-shell and DKI model to the complete set of multi-shell measurements, deriving FA, axial/radial/mean diffusivity (AD/RD/MD) and axial/radial/mean kurtosis. A quantitative T2 index was also obtained by fitting mono-exponential decay to the set of b = 0 images acquired at various TEs.

Model fitting was performed with custom-written python code (T1, T2, T2*, PD) and with FSL dtifit (FA, AD, RD, MD) and DiPy (AK, RK, MK).

Finally, a mask of two samples was drawn manually with FSLView and median and IQR of all metrics was evaluated within the masks.

RESULTS

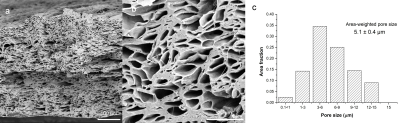
Fig.1 reveals axially-aligned hollow fibres and the range of their pore sizes. There is a broad range of pore sizes within the phantom, reminiscent of axonal distributions in spinal cord.⁷ The area-weighted pore size of hollow fibres was 5.1 ± 0.4 μm, which is much smaller than those used in brain phantoms.¹⁰

Figure 2 shows a sagittal view of the two samples and the conventional DTI colour-encoding, which highlights a much stronger directional coherence for the fibres within the sample that does not contain crossings.

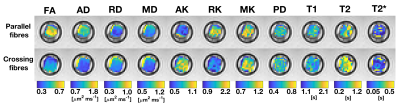
Figure 3 shows quantitative maps in both samples (diffusion metrics were resampled to the SPGR space for visualisation), while Table 1 reports median and IQR of all metrics. Diffusion properties differ considerably in the two samples due to their different fibre microstructure. The sample containing crossing fibres shows considerably smaller FA and AD and higher AK than the other sample. Overall, DTI and DKI metrics fall in a range that is compatible with values that could be observed in vivo.¹¹ The two samples show instead comparable relaxation properties, with relaxation constants longer than that observed in spinal cord white matter in vivo.¹²

DISCUSSION

The development of clinical spinal cord phantoms requires not only appropriate microstructures and orientation, but also sufficient bulk material to be used with clinical imaging protocols. The macro- and microstructures of microfibres can be effectively controlled using co-electrospinning,⁵ and have similar microstructure to spinal cord axonal structure, as demonstrated using SEM. The similarity in geometry is reflected in the similarity between our phantom diffusion parametrisations using a ZOOM acquisition and those seen in vivo.

CONCLUSION

A novel spinal cord-mimicking phantom has been developed, reflecting in vivo diffusion. The phantom exhibits diffusivity and anisotropy that are in the range expected for spinal cord, indicating that they can provide a helpful standard for diffusion measurements on clinical MR scanners.

Acknowledgements

This research was supported by NIHR UCLH Biomedical Research Centre (BRC) grant. GJM Parker has a shareholding and part time appointment and directorship at Bioxydyn Ltd. which provides MRI services. FG is funded by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 634541 and by the Engineering and Physical Sciences Research Council (EPSRC EP/R006032/1). The QSMSC is supported by the UK Multiple Sclerosis Society (grants 892/08 and 77/2017) and by the Department of Health's National Institute for Health Research (NIHR) Biomedical Research Centres (BRC R&D 03/10/RAG0449). The contribution from Marco Battiston and Becky Samson to the MR sequences is acknowledged. We thank Claudia Wheeler-Kingshott for allowing us total freedom to acquire MR data. We also thank Philips Healthcare for assistance in protocol development and for access to research protocols.