Introduction

Diffusion weighted imaging (DWI) has played important roles in the multiparametric MRI especially in cancer detection [1], however, widely-used ss-EPI DWI is usually susceptible to strong magnetic artifacts, and geometric distortion. Integrated slice dependent shimming (iShim) is a new technique to reduce magnetic field inhomogeneity and geometric distortion [2]. Moreover, recent study showed that iShim-EPI DWI has better image quality and SNR compared to ss-EPI DWI [1]. In this study, we aim to evaluate and quantify the in-plane and through-plane geometric distortion in EPI-DWI using iShim.

Methods

An ACR large MRI phantom was positioned (a) parallel, and (b) perpendicular to B0 (Figure 1). EPI-DWI Images were axially acquired for each phantom position (TR/TE = 5300/100 ms, voxel size=2x2x5 mm3, phase encoding (PE) direction=anterior-posterior, b=0 (NSA=2) and 700 (NSA=4) s/mm2, 21 slices, geometric distortion correction = ON, GRAPPA factor from iPAT 1 to iPAT 5) using iShim on a 1.5T MR scanner (Siemens Healthineers, Erlangen, Germany) with an 18-channel body coil. Axial 3D T1-weighted GRE images (TR/TE = 4.76/2.24 ms, voxel size = 0.8 x 0.8 x 1 mm3, flip angle= 100) were also acquired in both phantom positions as the reference. For each GRAPPA factor, the phantom was scanned twice to test the repeatability of geometric distortion. The through-plane geometric distortion (PE: ΔPEth, SE: ΔSEth), and in-plane geometric distortions (PE: ΔPEin, FE: ΔFEin) were measured by the absolute positional shift of the 109 intersection points on the grid at b=0s/mm2 (b0) and 700s/mm2 (b700) images with respect to the axial T1-weighted images.

The geometric distortion with different GRAPPA factors were compared using ANOVA test with Bonferroni correction as post-hoc. Intraclass correlation coefficient (ICC) was also calculated for distortion repeatability evaluation. Pearson correlation coefficient was conducted to evaluate the correlation between the acceleration factors and the geometric distortion. The magnitude of distortion was also evaluated in relation to its distance to iso-center.

Results

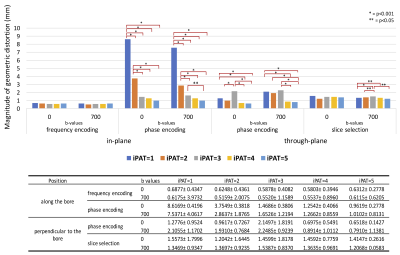
There was no statistically significant difference in the in-plane geometric distortion among all acceleration factors in the frequency encoding (FE) direction using b0 images (Fig. 2). However, statistically significant larger ΔPEin was observed in b0 scans using iPAT1 (8.6169±0.4196mm) comparing to higher acceleration factors (iPAT2:3.7549±0.3818mm, p<0.001; iPAT3:1.4686±0.3806mm, p<0.001; iPAT4:1.2542±0.4066mm, p< 0.001; iPAT5: 0.9619±0.2778mm, p<0.001). Similar trend was found in b700 scans with significantly larger ΔPEin using iPAT1:7.5317±4.0617mm than other acceleration factors (iPAT2: 2.8637±1.8765mm, p<0.001; iPAT3: 1.6526±1.2194mm, p<0.001; iPAT4: 1.2662±0.8559mm, p<0.001; iPAT5: 1.0102±0.8131mm, p<0.001). No significant difference in ΔPEin was observed between iPAT5 and IPAT4 (p=1.00).

When the acceleration factor increased, decreasing ΔPEin was also found to be statistically significant in both b-values as shown in figure 3(b-0: Pearson Coef.=-0.709(p<0.001) and b700: Pearson Coef.=-0.640(p<0.001)).

For through-plane distortion, larger ΔSEth (1.5573 ± 1.7996 mm) and ΔPEth (1.2776 ± 0.9524 mm) were found for iPAT1 than iPAT2 (ΔSEth 1.2042 ± 1.6445, p=0.114; ΔPEth = 0.9617 ± 0.7267, p=0.510), iPAT3 (ΔSEth= 1.4599 ± 1.8178, p<0.001; ΔPEth = 2.1497 ± 1.8191, p=0.132), iPAT4 (ΔSEth=1.4592 ± 0.7759, p=1.000; ΔPEth = 0.6975 ± 0.5491, p<0.001 ) and iPAT5 (ΔSEth= 1.4147 ± 0.2616, p=0.433; ΔPEth =0.6518 ± 0.1427, p<0.001). This decrease of ΔSEth and ΔPEth were more obvious in b700 than b0 (Fig. 4). The correlations between ΔPEth and acceleration factor are -0.172 (p<0.001) for b0 and -0.362 (p<0.001) for b700. The correlations between ΔSEth and acceleration factors were -0.22 (p=0.468) for b0 and 0.063 (p<0.05) for b700.

The distortion repeatability between two repeated scans was high for all acceleration factors (ICC=1; p<0.001) for all scans.

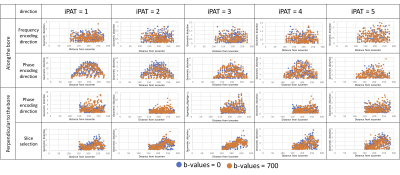
As illustrated in figure 5, the geometric distortion was seen to be more uniform across the frequency encoding direction and phase encoding direction in position (a) despite longer distance from iso-center. However, in position (b), larger geometric distortion was observed when the distance from the iso-center was larger.

Discussions

Small geometric distortion was observed for the in-plane FE, through-plane PE and through-plane SE, but not ΔPEin. However, ΔPEin reduction was observed when echo train length was reduced by applying GRAPPA. ΔPEth, was intrinsically less distorted due to the better B0 field adjustment along the slice direction using iShim. This, thus, explained the observed the weak dependence between ΔPEth and acceleration factor.

Excellent repeatability (ICC = 1) for all measurements indicated a highly repeatable geometric distortion pattern and reproducible B0 field shimming by iShim. Further optimization on the scan parameter should still be done for clinical application.

In this study, distortion measurement accuracy was limited by the relatively large EPI-DWI voxel size. Distortion in the larger FOV was limited by the size of the ACR MRI phantom. In vivo validation and evaluation are warranted.

Conclusions

Geometric distortion with iShim was quantitatively measured and characterized. Although small through-plane geometric distortion was achieved using iShim, in-plane geometric distortion minimization along phase encoding with high acceleration factor might be the major advantage by using iShim.

Acknowledgements

No acknowledgement found.