4495

3D-printed phantom for validating diffusion MRI models

Michael Woletz¹, Franziska Gantner^2,3, Benedikt Hager⁴, Peter Gruber^2,3, Siawoosh Mohammadi^5,6, Zoltan Nagy⁷, Aleksandr Ovsianikov^2,3, and Christian Windischberger¹
¹Center for Medical Physics and Biomedical Engineering, Medical University of Vienna, Vienna, Austria, ²Institute of Materials Science and Technology, Technical University Vienna, Vienna, Austria, ³Austrian Cluster for Tissue Regeneration, Vienna, Austria, ⁴Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Vienna, Austria, ⁵Department of Systems Neuroscience, University Medical Center Hamburg-Eppendorf, Hamburg, Germany, ⁶Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, ⁷Laboratory for Social and Neural Systems Research (SNS Lab), University of Zurich, Zurich, Switzerland

Synopsis

Here we show the first DTI phantom manufactured by advanced high-resolution 3D-printing methods. The phantom consists of hollow, 12μm thin, liquid filled channels, that can be constructed in arbitrary configurations, ideally suited for validating diffusion sequences and analysis models. A simple configuration with orthogonal channel directions is presented. Diffusion weighted images were acquired and a diffusion tensor model employed. The main direction of the resulting tensors is accurately able to capture the directions of the channels with an average fractional anisotropy of 0.46. This method for creating diffusion phantoms will help to test and validate different models in the future.

Introduction

Diffusion weighted imaging¹ (DWI) is an important scientific and diagnostic tool with a multitude of applications ranging from the exploration of white matter in the brain to characterising lesions and tumours²in the whole body. Beside the commonly used diffusion tensor imaging (DTI) model³ and tractography⁴ models, parameters that are supposedly more specific to micro-structure properties such as the fiber dispersion^5,6 can be estimated from DWI. For validating the specificity of the latter category of models as well as for testing the sensitivity of novel diffusion-weighted MR sequences, diffusion phantoms are needed for which the microscopy composition is well defined. Here we present a novel diffusion phantom manufactured with high-resolution 3D-printing technology that is capable of producing precise, arbitrarily-oriented structures.

Methods

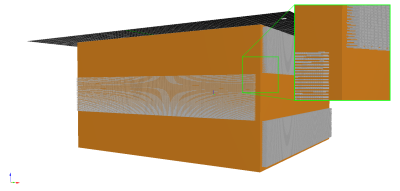
Diffusion phantoms were fabricated using multi-photon lithography (MPL)⁷. For this 3D-printing technique, femtosecond laser pulses are used to induce localised cross-linking by multi-photon absorption⁸. MPL allows the creation of structures with high definition features down to 100 nm making it possible to manufacture objects that contain complex networks of channels that resemble axons. To overcome constrains in fabrication times and sizes two MPL-upscaling-techniques were combined^9,10, enabling the production of MPL-objects with high-volume and high-definition features. The material used to fabricate the phantoms was a mixture of Ethoxylated trimethylolpropane triacrylate (ETA) and Trimethylolpropane triacrylate (TTA) in a ratio of 25:75 and M2CMK (5 mmol/g) as photoinitiator.
The overall size of the presented phantom was 6 mm x 6 mm x 3 mm. Fibre-like channels were fabricated in three distinguished areas (each 996 µm x 5792 µm x 6000 µm) within the phantom. Channels in area 1 and 3 were directed orthogonal to the channels in area 2. The channels were rectangular shaped with a cross section of 12 µm x 12 µm. The distances between the channels were 12 µm in vertical and 5 µm in lateral direction. Leading to 14 322 diffusion channels per area and a total of 42 966 channels with a density of 2483 channels/mm². An illustration of the phantom can be seen in Fig 1.
For the DWI-measurements, the channels were filled with a 20 mmol/l solution of copper(II)sulfate and PBS. The entire phantom was embedded in 7% gelatin from porcine skin mixed with PBS and copper(II)sulfate (20 mmol/l).
MR measurements were acquired at 7T (Magnetom Siemens Healthineers, Erlangen, Germany) using a microimaging system (gradient strength: 750 mT/m) and a 39 mm proton NMR volume coil (Rapid Biomedical, Wuerzburg, Germany). Morphological images were generated using a spin-echo sequence (4s TR, 6.6ms TE, 47x47µm² in-plane pixel resolution, 400µm slice thickness). DWI weighted images were acquired using a single shot, diffusion-prepared EPI imaging sequence (CMRR multiband sequence¹¹, 4s TR, 34ms TE, 322x322µm² in-plane pixel resolution, 322µm and 644µm slice thickness, 64 diffusion directions, 1250 and 2500 s/mm² b-values, two phase encoding directions), one slice per area of the phantom (total of 3 slices).
Diffusion-weighted images were analysed using a DTI model in dipy¹² after correcting for field inhomogeneities using FSL’s topup tool¹³. The tensor-based metrics, fractional anisotropy (FA) and mean diffusivity (MD) were estimated and summary statistics were computed inside and outside of the phantom.

Results

Morphological images can be seen in Fig 2. The stabilising borders along the directions of the channels as well as the individual regions of the MPL-upscaling-techniques are clearly visible. The diffusion tensor results can be seen in Fig 3, showing the first eigenvectors of the diffusion tensors in the three different areas. The distribution of the eigenvectors inside and outside of the phantom in spherical coordinates can be found in Fig 4. Values for FA and MD in the same regions can be found in Fig 5.

Discussion

We have successfully created a novel phantom for diffusion MRI by using advanced, high-resolution 3D-printing technologies. It contains liquid-filled channels in a 3D-printed surrounding, and it can be created in arbitrary configuration. Here we showed a simple configuration of sections with orthogonal directions. The employed DTI model was able to accurately capture this configuration and therefore show the phantom’s utility for diffusion imaging studies. Average fractional anisotropy inside the phantom was calculated with 0.46, showing intermediate anisotropy. This value depends on the channel configuration and can be adjusted accordingly. All diffusion tensors are clearly oriented parallel to channels, as can be seen from the plots in Fig 4.

Conclusion

We have developed the first 3D-printed DWI phantom with micrometer resolution and channels that approach physiological sizes. The phantom is useful for testing diffusion imaging acquisition and analysis methods because the size, orientation, density and arrangement of the channel structure can be predetermined and manufactured with high precision. In this work the proof of principle is presented. The materials for the 3D phantom were carefully selected through thorough testing to ensure they are compatible with MR imaging methods. Our future plans include printing different blocks with varying arrangements (e.g. crossing/kissing channel orientations) which could be tested simultaneously in an imaging experiment with a larger field of view. We envision the phantom being useful in translating imaging methods from basic research to clinical applications because with the ground-truth known, diffusion imaging methods can be more reliably tested against.

Acknowledgements

This project was funded under AWS-PRIZE P1621688-WZP01.

ZN was supported by Swiss National Science Foundation (grant nr: 31003A_166118).

References

1. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. The Journal of Chemical Physics. 1965; 42(1): 288-292.

2. Baliyan V, Chandan JD, et al. Diffusion weighted imaging: Technique and applications. World J Radiol. 2016; 8(9): 785-798.

3. Basser PJ, Mattiello J, et al. Estimation of the Effective Self-Diffusion Tensor from the NMR Spin Echo. Journal of Magnetic Resonance, Series B, 1994; 103(3): 247-254.

4. Farquharson S, Tournier JD, et al. White matter fiber tractography: why we need to move beyond DTI. Journal of Neurosurgery. 2013; 118(6): 1367-1377.

5. Zhang H, Schneider T, et al. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012; 61(4): 1000-1016.

6. Edwards LJ, Pine KJ, et al. NODDI-DTI: Estimating Neurite Orientation and Dispersion Parameters from a Diffusion Tensor in Healthy White Matter. Front Neurosci. 2017; 11: 720.

7. Stampfl J, Liska R, Ovsianikov A. Multiphoton Lithography: Techniques, Materials, and Applications. John Wiley & Sons. 2016.

8. Zhou X, Hou Y, et al. A review on the processing accuracy of two-photon polymerization. AIP Advances. 2015; 5(3).

9. Malinauskas M, Purlys V, et al. Two-photon polymerization for fabrication of three-dimensional micro- and nanostructures over a large area. Proc. SPIE 7204. 2009.

10. Obata K, El-Tamer A, et al. High-aspect 3D two-photon polymerization structuring with widened objective working range (WOW-2PP). Light Sci Appl 2. 2013.

11. Setsompop K, Cohen-Adad J, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage. 2012; 63(1): 569-580.

12. Garyfallidis E, Brett M, et al. DIPY, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics. 2014; 8(8).

13. Smith SM, Jenkinson M, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004; 23(S1):208-219.

Figures

Fig 1: Illustration of the DWI phantom and its sections. For better illustration, a part of the phantom was highlighted.

Fig 2: Morphological images of the DWI phantom in a) transversal and b) sagittal direction. The slices in a) represent the three areas of the phantom. The direction of the channels can be determined from the direction of the darker borders. The borders between the three areas is clearly visible in b).

Fig 3: Directions of the first eigenvectors of the DTI model estimated from the DWI images. The columns panel represent the slices, corresponding to the three areas. The rows were generated from the data with 322 μm and 644 μm slice thickness respectively. The eigenvectors were coloured with their respective orientations (mix of red, green and blue, representing x, y and z directions, see inset in the lower right) and scaled by the fractional anisotropy.

Fig 4: Kernel density distribution estimates of the DTI model’s first eigenvector in spherical coordinates. The columns in each panel represent the slices and therefore the three areas of the phantom. The rows were generated from the data with 322 μm and 644 μm slice thickness respectively. a) The distribution of φ. b) The distribution of θ.

Fig 5: Fractional anisotropy (FA) and mean diffusivity (MD) for the different measurements and slices (areas) of the phantom, inside the phantom and outside of the phantom (in the gelatin).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4495