4493
Diffusion MRI-based Connectivity Enriched with Microstructure Information Predicts the Propagation of Cortico-Cortical Evoked Potentials1INRIA Sophia Antipolis - Méditerranée, Valbonne, France, 2Service de Neurochirurgie, Centre Hospitalier Universitaire de Nice, Université Côte d’Azur, Nice, France, Nice, France, 3Service de Radiologie, Centre Hospitalier Universitaire de Nice, Université Côte d’Azur, Nice, France, Nice, France, 4INRIA, CEA, Université Paris-Saclay, Paris, France, Paris, France
Synopsis
The propagation of Cortico-Cortical Evoked Potentials (CCEPs) varies depending on numerous structural features of brain tissue. In this work, we show that combined dMRI-based connectivity enriched with microstructure data has the potential to measure cortico-cortical communication as it predicts CCEP-based effective connectivity. Our multiple linear regression model incorporates q-space indices like Q-space Inverse Variance, Non-Gaussianity and Return to Plane Probability with minimum streamline lengths obtained from tractography to predict delays and amplitudes of the P1 peaks in CCEPs. In our experiment, we use presurgical dMRI and intrasurgical ECoG recordings of 9 patients operated on brain tumor in the awake condition.
INTRODUCTION
The propagation of Cortico-Cortical Evoked Potentials (CCEPs) varies depending on numerous structural features of the brain tissue [1,2]. In this work, we show that combined dMRI-based connectivity enriched with microstructure data has the potential to measure cortico-cortical communication as it predicts CCEP-based effective connectivity. For this, we studied a group of 9 patients undergoing brain tumor resection in the wide awake condition.METHODS
For each of the 9 patients (5 female, aged 40±13), we acquired presurgical multishell dMRI (b∈{400,800,1550,3100}[s/mm2] with {6,13,29,51} directions, respectively) and intrasurgical ECoG recordings in the exposed perisylvian language area (Figure 1). Direct Electrical Stimulation (DES) of the cortex induced a series of repetitive CCEPs, which we quantified with delays and amplitudes of P1 peaks [1,3]. Then, we trained linear regression models to predict the above effective connectivity measures using variables describing structural links between DES sites and ECoG recording electrodes, i.e. (i) log-transformed streamline counts, (ii) minimum and (iii) median streamline lengths, (iv) distances measured along the surface of white matter (WM).Taking into account that propagation of evoked potentials is related to tissue microstructure [4], we extended our set of variables obtained from dMRI with common tensor-based and q-space indices: Fractional Anisotropy (FA); Mean (MD), Axial (AD), and Radial Diffusivities (RD); Return to Origin (RTOP), Axis (RTAP), and Plane Probabilities (RTPP); Mean Squared Displacement (MSD), Q-space Inverse Variance (QIV), Non-Gaussianity (NG), and parallel (NG||) and perpendicular Non-Gaussianity (NG_|_). Our approach was strictly data-driven. We applied stepwise regression on the full set of indices for a feature selection. Also, we arranged the streamlines in the ascending order with respect to their lengths and tested various subsets of streamlines restricted with low-pass and high-pass filters with cut-off values defined by percentiles of lengths plower, pupper∈{0,10,20,...,100}.
RESULTS
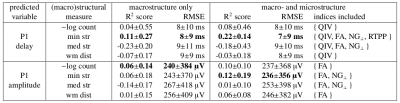
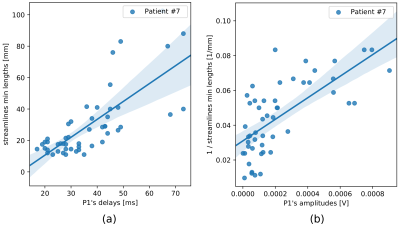
The linear regression models which used macrostructure information only produced comparable mean residuals for each of the four input measures, nonetheless a dispersion of residuals was relatively high (Table 1). Variances of the effective connectivity data were best explained by minimum streamline lengths (Figure 2), for which R2-scores were the highest (Table 1).The stepwise regression method gave consistent results regarding microstructure features selection (Table 1): QIV was chosen in all the four models aimed at predicting P1 delays, while FA, NG_|_, and RTPP appeared in the models based on the streamline lengths. Analogously, for predicting P1 amplitudes, the stepwise regression method selected FA and NG_|_.
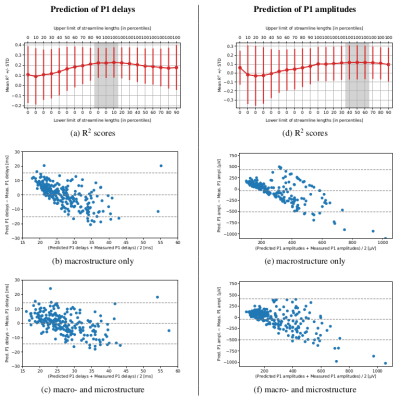
The models based on a combination of macro- and microstructure data reached higher prediction accuracy than the ones using macrostructure only. However, their performance varied depending on the length of streamlines along which the microstructure indices were computed (Figure 3). While predicting the P1 delays with minimum streamline lengths and {QIV, FA, NG_|_, RTPP}, the R2-scores were highest and least dispersed when all the streamlines were included. Meanwhile, for predicting the P1 amplitudes, it was better to remove a shorter half of the streamlines from the data set. Also note that the macrostructure only models visibly overestimated the low values of P1 delays and P1 amplitudes, yet understimated the high ones (Figure 3). An inclusion of the microstructure indices helped reduce this bias.
DISCUSSION
We hypothesized that the propagation of P1 peaks in CCEPs depends on the macro- and microstructural properties of the WM fibers connecting the pyramidal cells excited with DES and the distal recording areas. The observed increases of the R2-scores and decreases of the mean squared residuals after including the microstructure-related indices in our linear regression models imply tangibly that these variables contained information about the propagation of CCEPs and thus can serve as a measure of cortico-cortical comunication.The presence of FA among the features selected with the stepwise regression method is by far the most intuitive. This tensor-based index relates, although non-specifically, to numerous properties of WM microstructure, including fiber density, neurites dispersion, axonal diameter, and myelination level [5]. Also note that QIV appeared systematically in all the studied regression models for the P1 delays. As pointed out by Fick et al. [6], this index reflects changes in tissue composition and is probably more sensible in doing so than FA. Another notable example is RTPP which is typically attributed to the length of a pore [7]. Additionally, it doesn't require an angular integral and doesn't suffer from the power law phenomena [8]. However, RTPP feature was selected only once, so its relevance in predicting the effective connectivity measures might be questionable. Finally, the role of NG_|_ is most difficult to interpret. This index quantifies the non-Gaussian, hence restricted, portion of the diffusion signal measured perpendicularly to the principal fiber direction. However, one must keep in mind that NG_|_ is computed under the assumption of an axial symmetry of a tissue, which is often not satisfied.
CONCLUSION
In this study, we showed that brain tissue microstructure features help explain the propagation of CCEPs. Particularly, the P1 delays and amplitudes measured instrasurgically in brain tumor patients were linearly related to FA and q-space indices quantifying axon dispersion and WM tissue composition. We believe that our findings extend the clinical significance of microstructure indices and contribute to the goal of understanding the propagation of CCEPs.Acknowledgements
This work has received funding from the ANR/NSF award NeuroRef; the MAXIMS grant funded by ICM's The Big Brain Theory Program and ANR-10-IAIHU-06.References
[1] C. J. Keller, C. J. Honey, P. Mégevand, L. Entz, I. Ulbert, A. D. Mehta, Mapping human brain networks with cortico-cortical evoked potentials, Phil. Trans. R. Soc. B 369 (2014).
[2] Y. Yamao, R. Matsumoto, T. Kunieda, Y. Arakawa, K. Kobayashi, K. Usami, S. Shibata, T. Kikuchi, N. Sawamoto, N. Mikuni, et al., Intraoperative dorsal language network mapping by using single-pulse electrical stimulation, Human brain mapping 35 (2014) 4345-4361.
[3] M. Vincent, D. Guiraud, H. Duffau, E. Mandonnet, F. Bonnetblanc, Electrophysiological brain mapping: Basics of recording evoked potentials induced by electrical stimulation and its physiological spreading in the human brain, Clinical Neurophysiology 128 (2017) 1886-1890.
[4] L. Goldman, J. S. Albus, Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation, Biophysical journal 8 (1968) 596-607.
[5] P. J. Basser, C. Pierpaoli, Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor mri, Journal of magnetic resonance 213 (2011) 560-570.
[6] R. H. J. Fick, M. Pizzolato, D. Wassermann, M. Zucchelli, G. Menegaz, R. Deriche, A sensitivity analysis of q-space indices with respect to changes in axonal diameter, dispersion and tissue composition, in: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), IEEE, pp. 1241-1244.
[7] E. Özarslan, C. G. Koay, T. M. Shepherd, M. E. Komlosh, M. O. İrfanoğlu, C. Pierpaoli, P. J. Basser, Mean apparent propagator (MAP) MRI: A novel diffusion imaging method for mapping tissue microstructure, NeuroImage 78 (2013) 16-32.
[8] J. Veraart, E. Fieremans, D. S. Novikov, Universal power-law scaling of water diffusion in human brain defines what we see with MRI, arXiv preprint arXiv:1609.09145 (2016).
Figures
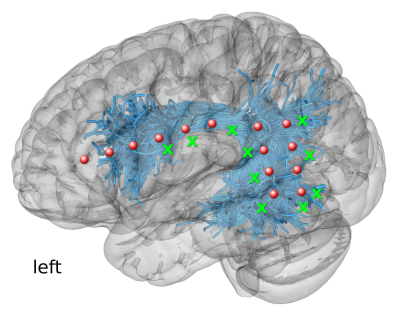
Figure 1. ECoG electrodes for recording CCEPs in Patient 1. The scheme illustrates the presurgical planning of the locations of electrodes (red circles) and stimulation sites (green crosses) using the tractography-based dissections of Arcuate Fasciculus and Superior Longitudinal Fasciculus III (both pictured jointly as blue streamlines)