4491

Diffusion MRI simulation of realistic neurons with SpinDoctor and the Neuron Module

Van-Dang Nguyen¹, Chengran Fang^2,3, Demian Wassermann³, and Jing-Rebecca Li²
¹Department of Computational Science and Technology, KTH Royal Institute of Technology, Stockholm, Sweden, ²INRIA-Saclay, Equipe DEFI, Palaiseau, France, ³INRIA Saclay, Equipe Parietal, Palaiseau, France

Synopsis

The dMRI simulation arising from realistic neurons can help investigate the cellular microstructure. Ensuring correct connectivity between distinct cellular compartments while minimizing the computational burden is one of the main challenges. The design of simulation algorithm and the construction of high-quality neuron meshes are crucial. The NeuronModule can perform HARDI simulation of realistic neurons at various b-values and diffusion sequences with high accuracy. The computational time per gradient-direction is around 30 seconds which is faster than some Monte-Carlo simulators. The linearity between the diffusion-direction-averaged signal and one over square root of b for tubular structures is validated by our simulations.

INTRODUCTION

The simulation of diffusion MRI arising from realistic neuron models can help investigate the cellular microstructure^{1, 2}. However, ensuring correct connectivity between the distinct compartments comprising the system while minimizing the computational burden is one of the main challenges in our community³. The design of an accurate and efficient simulation algorithm and the construction of high-quality neuron meshes are two difficulties in addressing this problem. Our previous work includes a MATLAB Toolbox called SpinDoctor that is a diffusion MRI simulation pipeline based on solving the Bloch-Torrey partial differential equation using finite elements and an adaptive time stepping method⁴. The first version of SpinDoctor focuses on the brain white matter whose biophysical models subdivide the tissue into compartments described by ellipsoids, cylinders, and the extra-cellular space. In this study, we present a new module of SpinDoctor called the Neuron Module that enables neuron simulations for a group of 36 pyramidal neurons and a group of 29 spindle neurons whose morphological descriptions were found in the publicly available neuron repository NeuroMorpho.Org⁵.

METHODS

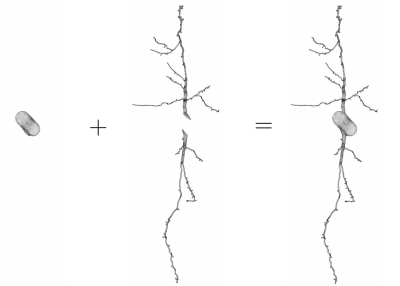
The key to making accurate simulation possible is the use of high-quality meshes for the neurons. For this, we started with the morphological reconstructions published in NeuroMorpho.Org⁵. These surface descriptions contain many self-intersections and proximities. We then used licensed software from ANSA-BETA CEA Systems⁶ to correct and improve the quality of the neuron surface descriptions and produced new surface triangulations that are ready to be used for finite elements mesh generation. The new surface triangulations are passed into the software GMSH⁷ to obtain volume tetrahedral meshes. To further study the diffusion MRI signal of neurons, we broke the neurons into disjoint geometrical components. As an illustration, we show in Figure 1 the spindle neuron 03a_spindle2aFI volume tetrahedral mesh broken into sub-meshes of the soma and the two dendrite branches.
These finite elements meshes are used as input files in the Neuron Module, where they can be further refined if required using the built-in option in SpinDoctor. Currently, the spin exchange across the cell membrane is assumed to be negligible in the Neuron Module. Through the Neuron Module, these neurons and components finite element meshes can be seamlessly coupled with the functionalities of SpinDoctor to provide the diffusion MRI signal attributable to spins inside neurons.

RESULTS

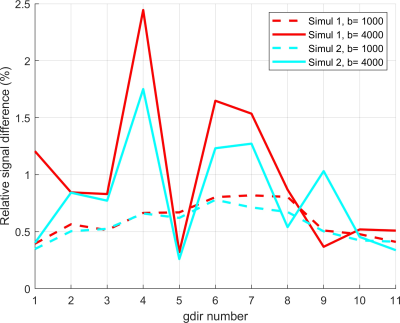
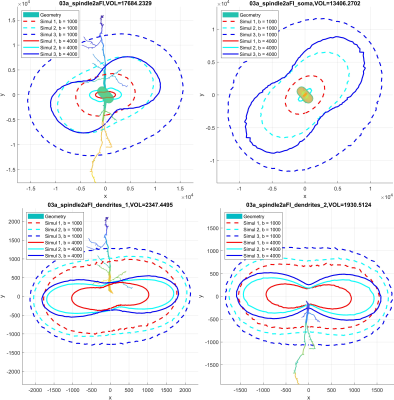
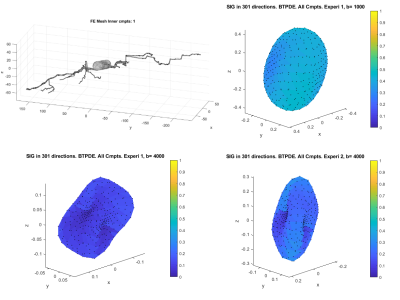
We first validate our simulations by refining in space (making the finite elements smaller) and refining in time (decreasing the error tolerance of the ODE solver). The reference signal has the finest finite element size and the smallest error tolerance among the simulated signals. The signal difference between the reference signal and the simulated signals for the neuron 25o_pyramidal18aFI is plotted in Figure 2. In this case, we see that the signal difference is less than 2.5% for b = 4000s/mm² and less than 1% for b=1000 s/mm². In Figure 3 and Figure 4, we show 2D and 3D high angular resolution diffusion imaging simulations respectively. The average computational time per gradient direction is around 30 seconds which is much faster than the Monte-Carlo simulations using Camino⁴. By visual inspection, the signals in the whole neuron are close to the volume weighted sums of the signals from the three geometrical components.
In [8] it was shown experimentally that the diffusion MRI signal of tubular structures such as axons exhibits a certain high b-value behavior, namely, the diffusion direction averaged signal, $$$S_{ave} (b)$$$, is linear in $$$\dfrac{1}{\sqrt {b}}$$$ at high b-values. Because the dendrites of neurons also have a tubular structure, we test whether the diffusion direction averaged signal, $$$S_{ave} (b)$$$, of dendrite branches also exhibits the above high b-value behavior. We computed $$$S_{ave} (b)$$$ for the neuron 03a_spindle2aFI as well as their associated dendrite branches averaged over 31 diffusion directions uniformly distributed in three dimensions. The results are shown in Figure 5. We see clearly the linear relationship between $$$S_{ave} (b)$$$ and $$$\dfrac{1}{\sqrt {b}}$$$ in the dendrite branches for b-values in the range $$$2500 s/mm^2 \leq b \leq 20000 s/mm^2$$$. In contrast, in the whole neuron, due to the presence of the soma, such linear relationship is not exhibited.

CONCLUSION

We presented the Neuron Module which we implemented in the Matlab-based diffusion MRI simulation toolbox SpinDoctor. We have created high-quality volume tetrahedral meshes for a group of 36 pyramidal neurons and a group of 29 spindle neurons. In the current study, we illustrated the usefulness of the Neuron Module in providing simulated HARDI signals at various b-values and diffusion times. In addition to calculating the HARDI signals from whole neurons, we also simulated the HARDI signals of neuron components such as the soma and the dendrite branches. In particular, we compared the high b-value behavior of the diffusion MRI signals from dendrite branches and from whole neurons, confirming the linear relationship between the diffusion direction averaged signal and $$$\dfrac{1}{\sqrt {b}}$$$ for tubular structures. These meshes and the source code of the Neuron Module are made available to the public as an open-source package⁹.

Acknowledgements

Van-Dang Nguyen was supported by the Swedish Energy Agency with the project ID P40435-1 and MSO4SC, the grant number 731063. We would like to thank ANSA from Beta-CAE Systems S. A., for providing an academic license.

References

1. Mercredi M, Martin M. Toward faster inference of micron-scale axon diameters using Monte Carlo simulations[J]. Magnetic Resonance Materials in Physics, Biology and Medicine, 2018, 31(4): 511-530.

2. Rensonnet G, Scherrer B, Warfield S K, et al. Assessing the validity of the approximation of diffusion‐weighted‐MRI signals from crossing fascicles by sums of signals from single fascicles[J]. Magnetic resonance in medicine, 2018, 79(4): 2332-2345.

3. Palombo M, Alexander D C, Zhang H. A generative model of realistic brain cells with application to numerical simulation of the diffusion-weighted MR signal[J]. NeuroImage, 2019, 188: 391-402.

4. Li J R, Nguyen V D, Tran T N, et al. Spindoctor: A matlab toolbox for diffusion mri simulation, NeuroImage 202 (2019) 116120. doi:https://doi.org/10.1016/j.neuroimage.2019.116120.

5. Ascoli G A, Donohue D E, Halavi M. NeuroMorpho. Org: a central resource for neuronal morphologies[J]. Journal of Neuroscience, 2007, 27(35): 9247-9251.

6. BETA C A E. Systems, ANSA the advanced CAE pre-processing software for complete model build up[J]. 2016.

7. Geuzaine C, Remacle J F. Gmsh: A 3‐D finite element mesh generator with built‐in pre‐and post‐processing facilities[J]. International journal for numerical methods in engineering, 2009, 79(11): 1309-1331.

8. Veraart J, Fieremans E, Novikov D S. On the scaling behavior of water diffusion in human brain white matter[J]. NeuroImage, 2019, 185: 379-387.

9. https://github.com/jingrebeccali/SpinDoctor/tree/NeuronModule

Figures

Figure 1: The volume tetrahedral mesh of the spindle neuron 03a_spindle2aFI is broken into three geometrical components: the soma and two dendrite branches.

Figure 2: The signal differences between the reference signal and the simulated signals for the neuron 25o_pyramidal18aFI.

Figure 3: The diffusion MRI signals in 90 directions lying on the x-y plane, uniformly distributed on the unit circle. Top left: the whole neuron 03a_spindle2aFI. Top right: the soma. Bottom left: the upper dendrite branch. Bottom right: the lower dendrite branch.

Figure 4: Top left: the finite elements mesh of the spindle neuron 03a_spindle2aFI, the unit is micron. The other three plots: HARDI simulations in 301 diffusion directions. The color gives the magnitude of the signal attenuation.

Figure 5: The diffusion direction averaged signal, S_ave(S), as a function of one over the square root of b. The diffusion direction averaged signal is normalized so that S_ave(b=0)=1. The b-values are b={60000, 40000, 20000, 12000, 10000, 8000, 7000, 6000, 4000, 2500} s/mm².

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4491