Methodology

Purpose:
Diffusion tractography is routinely used to study white matter architecture and brain connectivity $$$\textit{in vivo}$$$ [2,3]. An essential component for successful tractography of neuronal tracts is the correct identification of the tract directionality in each voxel. However, accurate fiber direction estimation is difficult due to the limited angular resolution of the acquisition and intrinsic ODF peak width [4,5] and most methods fail to detect fibers crossing at angles smaller than 30°-40° [3,5]. Research has indicated that the ODF Fingerprinting methodology can improve the detection of these fiber crossings [1,7,8] by drawing a comparison between the measured ODF and the elements in a pre-generated library of ODF-fingerprints [9,10]. We applied this methodology in a clinical post-operative case to determine the feasibility of ODF-fingerprinting in comparison to several other fiber directionality identification algorithms $$$\textit{in vivo}$$$ .
Methods:
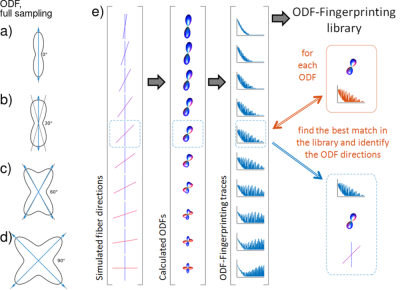
ODF-Fingerprinting: For ODF-Fingerprinting, a library $$$L_{ODF}$$$ was generated by utilizing diffusion weighted signals as a sum of diffusion tensors (FA$$$\,=\,$$$[0.3,1], ADC$$$\,=\,0.9\,\mathrm{mm^2/s}$$$, 10% water component, assumption of cylindrical fibers $$$\lambda_2=\lambda_3$$$) on a Radial Diffusion Spectrum Imaging grid (RDSI, 236 q-space samples, four shells, bmax=$$$4000\,\mathrm{s/mm^2}$$$) and reconstructing ODFs, as demonstrated in Figure 1 [11]. Matching of a measured $$$ODF_m$$$ with the elements of library $$$L_{ODF}$$$ was assessed by maximizing the dot-product [9,10] with an added penalty term for the noise estimate $$$\sigma_n$$$ of the input diffusion data: $$$\mathrm{max}\left(\log(L_{ODF}\,.\,ODF_m) – n_{par}/{4n} \sigma_n\right)$$$ ($$$n_{par} = 1 + 5N_{fib}$$$ a measure of library element complexity and $$$n$$$ the number of elements in $$$ODF_m$$$) [8]. $$$\sigma_n$$$ is estimated using a linear mean square error estimator for the variance of the noise of diffusion weighted signals [12]. The size of the fingerprint-library is reduced by rotating the maximum value of ODF-traces to the Z-axis before matching. The ODF fingerprinting method is compared with local maximum search (DSIStudio), Newton search along a set of specified directions (MRtrix3, $$$\mathrm{sh2peaks}$$$) and constrained spherical deconvolution (CSD, MRtrix3, $$$\mathrm{dwi2fod\,\,\,msmt\_csd}$$$ and $$$\mathrm{sh2peaks}$$$).
Data: An $$$\textit{in vivo}$$$ Radial DSI [11] dataset was acquired on a 3T clinical scanner (3T Siemens Prisma; 20ch head coil; b$$$_{max}\,=\,4000\,\mathrm{s/mm^2}$$$; 236 q-space volumes; TR/TE=2600/119; 45slices; $$$220\,\mathrm{mm}$$$ FoV; $$$3\,\mathrm{mm}$$$ isotropic resolution; PF5/8; male volunteer 60y/o). The images are denoised [14] and corrected for susceptibility, eddy currents and subject motion using eddy from the FSL Library [13]. RDSI reconstructions, incorporating variable sample density correction, were performed offline using custom-made software (Matlab, Mathworks). Display with Matlab and DSIStudio [Yeh2010].
Tractography: Corticospinal (CST), Arcuate Fasciculus (AF) and Optic Radiation (OR) tracts were generated using DSIStudio [Yeh2010] by seeding from the precentral lobe, the operculum and the visual cortex respectively. Fiber tracts are generated with a tracking algorithm (Yeh et al., 2013, implemented in DSIStudio (Yeh et al., 2010), parameters as suggested in (Fernandez-Miranda et al., 2012)) in both simulated and in vivo datasets. Tracts originate from random seeding points uniformly distributed in user-defined seeding regions, propagate along the most prominent fiber direction with a step size of 2 mm, are smoothed with 20% of the previous direction and halt when the turning angle > 60∘ or QA < 0.25. Resulting fiber tracts shorter than 20mm and longer than 400mm are discarded until a predetermined number of fiber tracts (1 10$$$^4$$$) is created or a maximum number of seed points is reached (1 10$$$^6$$$).

Results and Discussion

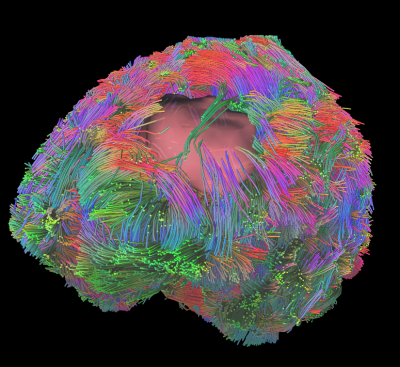
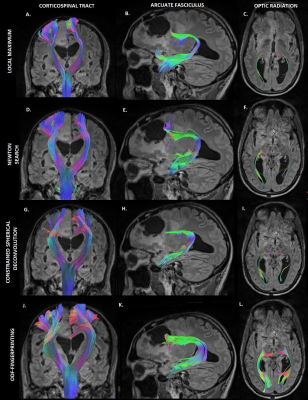
Figure 2 demonstrates the overall fiber tractography of the brain with a tumor embedded in the frontal lobe. The figure demonstrates how the fibers move around the tumor region, which aids in neurosurgical planning. The tracts analyzed by utilizing the ODF-Fingerprinting methodology demonstrate a fuller fanning of fiber groupings. The ODF-Fingerprinting also demonstrated improved fiber tractography in the various regions of interest (Corticospinal, Arcuate Fasciculus, and Optic Radiation) as shown in Figure 3. The figure compares the 3 other tractography methods to the ODF-Fingerprinting, and shows a fuller fanning in the regions of interest with ODF-Fingerprinting.

Conclusion

ODF-Fingerprinting has been shown to improve detection of fiber pairs with small crossing angles in simulations and qualitative evaluations of $$$\textit{in vivo}$$$ data. Here we show the application of ODF-FP $$$\textit{in vivo}$$$ in a clinical setting. The improved fiber identification by ODF-FP will aid neurosurgeons in pre-operative planning by generating improved renderings of brain connectivity. Future work will focus on examining additional clinical patients and on verifying the method in fiber phantoms.

Acknowledgements

This project is supported in part by PHS grants R01-CA111996, R01-NS082436 and R01-MH00380. DGP is supported by NIH/NINDS R01-NS102665, New York State DOH01-STEM5-2016-00221 and NIH/NIAID R21-AI130618. This work was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, https://www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41EB017183).