4470
RIPPLE: A new framework for estimating rotationally-invariant with paired-ODF spatial correlations in fiber tracking using MRI1Center for Biomedical Imaging, Department of Radiology, NYU School of Medicine, New York, NY, United States, 2Center for Advanced Imaging Innovation and Research (CAI2R), NYU School of Medicine, New York, NY, United States
Synopsis
Quantification of internal structure (i.e., microstructure) is central to for the modeling of diffusion signals. In recent years, rotationally-invariant measures have generated significant attention because of their tremendous potential for characterizing the underlying structural information contained in the orientation-distribution-function (ODF). We demonstrate the use of a new approach for the analysis of long-range structural connectivity based on the use of pairwise correlations between ODF’s. This approach is shown to better capture differences between the underlying morphological features present within a fiber bundle.
Purpose
Quantification of brain tissue structure (i.e., microstructure) is the central goal when modeling diffusion signals. In recent years, rotationally-invariant methods [1-2] have generated significant attention because of their tremendous potential for characterizing the underlying structural information at each voxel within a fiber bundle. We pose that by analyzing correlation between pairs of ODF’s the microstructure and angular information within a voxel can be better used to improve the accuracy of tractography algorithms. A framework for defining and computing paired-ODF correlations has not been previously presented. This work attempts to fulfill this need by introducing a framework, hereafter called Rotationally-Invariant with Paired-odf sPatiaL corrElations (RIPPLE), for the determination of long-range structural correlations in a fiber bundle.Methods
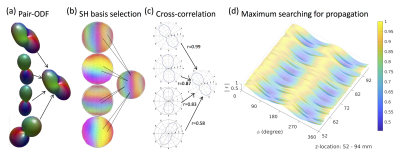
In vivo and simulated ODF’s were used to demonstrate the proposed method. In vivo dMRI acquisition was obtained from the Human Connectome Project (HCP). We used a single subject from the Human Connectome Project 900 subjects release (s900) dataset. Diffusion MRI scan parameters were 6 b0-images, 270 diffusion weighting directions, b-max=3000 s/mm, TR/TE=5520/89.5ms, 1.25mm resolution. Structural imaging (MPRAGE; 0.7mm isotropic resolution) was used for registration. The preprocessing pipeline included artifact removal, motion correction, and registration to the standard space. Simulated data (ODF’s) were generated using the Phantomas-software [3]. Simulated and in vivo ODF’s were processed using the same algorithm. In this algorithm, the tessellated ODF samples are restricted to $$$\theta$$$= 0 and 2$$$\pi$$$ in order to intersect the target x-z plane. The local fiber information is then obtained by using a spherical harmonic (SH) decomposition of order $$$l_{max}$$$=16 and thereby provide the ODF shape information on the target plane. ODF’s for performing the correlation analysis are then determined from the correlation analysis of the 8 nearest neighbors to the voxel of interest. The voxel with the highest correlation is then chosen as the one defining the tract direction and the tract orientation is determined by the correlation lag that yields the maximum value. This approach is expected to improve upon simple peak finding algorithms as the correlation analysis incorporates not only angular information but also the microstructural information contained in the ODF. Tract reconstructions were performed using custom-made software (Matlab, DSIStudio). Fiber tracts were generated using a deterministic tracking algorithm [4-5], and displayed with DSIStudio. Tracts originate from random seeding points uniformly distributed in user-defined seeding regions and propagate along the most prominent fiber direction with a step size of 0.6 mm, and halt when the turning angle > 600. Resulting fiber tracts shorter than 25 mm and longer than 500 mm are discarded until a predetermined number of fiber tracts 103 is created.Results and Discussion
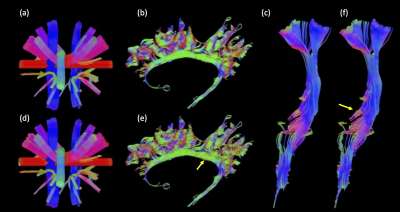
As expected, the cortico-spinal tract example (fig.1b-d) exhibits maximum correlations at $$$\phi$$$=0 (and 180 degrees), which reflects the up and down orientations of the tract. The proposed trajectory of the tract (in fig. 2d-f) is similar to the trajectory obtained using the peak-finding method utilized by the deterministic tracking algorithms (in fig. 2a-c). Note, however, that the method based on the ODF’s correlation captures important details about shape, size and relative displacements from the microstructure information along the track, which are not easily rendered using the conventional peak-finding method.Conclusion
RIPPLE is a method which provides improved directional information from ODFs for use in tractography. Our results show dispersion of the tracts at the level of the posterior limb of internal capsule (PLIC) in the cortical spinal tract (CST) [6] (fig. 2f), which cannot be rendered using the traditional peak finding approach. The RIPPLE method can be further improved by optimizing its operational parameters, adding additional constraints, such as anatomical features, or finding the best peak initialization using ODF-FP [7].Acknowledgements
This project is supported in part by PHS grants R01-CA111996 and R01-NS082436. HCP data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.References
[1] Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI, DS Novikov, J Veraart, IO Jelescu, E Fieremans, NeuroImage 174, 518-538, 2018.
[2] A closed-form solution of rotation invariant spherical harmonic features in diffusion MRI, M Zucchelli, S Deslauriers-Gauthier, R Deriche, International Conference on Medical Image Computing and Computer-Assisted Intervention, 77-89, Springer, 2018.
[3] E. Caruyer, A. Daducci, M. Descoteaux, J.-C. Houde, J.P. Thiran, R. Verna, Phantomas: a flexible software library to simulate diffusion mr phantoms, Proc. Intl. Soc. Magn. Reson. Med, vol. 21 (2014).
[4] F.C. Yeh, V.J. Wedeen, W.Y. Tseng, Generalized q-sampling imaging, IEEE Trans. Med. Imaging, 29 (9) (2010), pp. 1626-1635.
[5] F.C. Yeh, T. Verstynen, Y. Wang, J.C. Fernandez-Miranda, W.Y. Tseng, Deterministic diffusion fiber tracking improved by quantitative anisotropy, PLoS One, 8 (11) (2013), Article e80713.
[6] Groeschel S, Hagberg GE, Schultz T, Balla DZ, Klose U, et al. (2016) Assessing White Matter Microstructure in Brain Regions with Different Myelin Architecture Using MRI. PLOS ONE 11(11): e0167274.
[7] Steven H. Baete, Martijn A. Cloos, Ying-Chia Lin, Dimitris G. Placantonakis, Timothy Shepherd, Fernando E. Boada, Fingerprinting Orientation Distribution Functions in diffusion MRI detects smaller crossing angles, NeuroImage, Volume 198, 2019.
Figures