PURPOSE:

Double Diffusion Encoding(DDE) is a diffusion measurement technique that applies two directions of diffusion encoding in parallel and orthogonal directions. DDE can calculate μFA that can evaluate detailed information of anisotropy in voxels and was previously presented to improve lesion detection in oncology cases in the head. However, since the diffusion encoding method generally used the 5-design(the parallel 12 and orthogonal 12x5 diffusion encodings, totaling 72 directions)_[1], the acquisition time becomes long. It is necessary to shorten the acquisition time for clinical use. Recently various diffusion encoding patterns was proposed to shorten the acquisition time for the brain_[2]. Noise reduction technique is one of the methods to solve this problem. We have developed a denoising approach with deep learning reconstruction(dDLR), a noise reduction technique based on deep learning, using high SNR images and images with various intensities of noise added. In the present study we extended DDE technique, applying dDLR to original image, adapting it to the head. Improved acquisition time is achieved by adapting dDLR, while reducing the number of diffusion encodings and keeping the validity of μFA estimates. Results were tested on two healthy volunteers.

METHODS:

Theory: DDE sequence applies the diffusion encoding twice along two orientations before data acquisition. The μFA can be calculated by:

$$μFA=\sqrt{{\frac{3}{2}}\frac{μA}{μA+\frac{3}{5}\text{MD}^2}}\,\,\,\,\,\,\,\,\,\,\,(1)$$

Where MD stands for mean diffusivity and μA² and ε are following,

$$μA^2=\frac{ε}{∆}\,\,\,\,\,\,\,\,\,\,\,(2)$$
$$ϵ = \frac{\left[log\left( \frac{1}{N_{para}} ∑S_∥ \right)-log\left( \frac{1}{N_{ortho}} ∑S_⊥ \right) \right]}{ q^4}\,\,\,\,\,\,\,\,\,\,\,(3)$$

where S_∥ is signal with parallel diffusion encoding, S_⊥ is signal with orthogonal diffusion encoding, N_para is the Number of parallel diffusion encodings and N_ortho is the Number of orthogonal diffusion encodings.

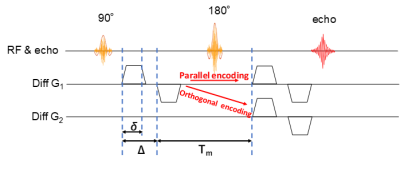
Volunteers study: The models described above were validated on two volunteers. Whole-brain axial scans were acquired on a clinical scanner(Vantage Galan 3T/ZGO, Canon Medical Systems Corp.) using a DDE-Single-shot SEEPI2D sequence(Fig.1). Acquisition parameters were: TR/TE=5000ms/101ms, FOV=24cm x 24cm, Matrix=80x80, slice-thickness/gap=3mm/0mm and b-value=0 and 2000s/mm² (for the entire of DDE). Parameters of diffusion time were δ=16ms, Δ=19ms and mixing-time=27ms.
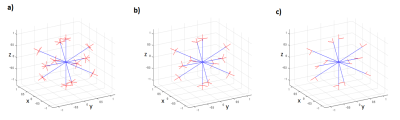
We compared three diffusion encoding schemes; the 5-design_[1], our proposed scheme and the minimal scheme proposed by Yang which are shown in fig.2. Our proposed scheme reduced the orthogonal diffusion encodings from five with the 5-design to three(Fig.2b). The minimal scheme used 12 symmetric acquisition for pattern B_[3] (Fig.2c). The acquisition time(the 5-design with 1 average, our proposed scheme with 1 average and the minimal scheme with 1 average) were 6:20, 4:10 and 2:10, respectively. Also, to evaluate μFA with similar SNR among each diffusion scheme, we matched total number of acquisitions for the 5-design, our proposed scheme and the minimal scheme as following, acquisitions in the 5-design were averaged 2 times(2NEX), acquisitions in our proposed scheme were averaged 3 times(3NEX) and acquisitions in minimal scheme were averaged 6 times(6NEX), totally 144 diffusion encodings in each scheme.
About dDLR method_[4][5], the input image is divided high and low frequency components using discrete cosine transforms(DCT). The Neural Network is trained to remove noise from the high frequency components, and to recover detail structures from the low frequency components. We used two strengths of dDLR(high and low). dDLR was adapted to original image with 1average(1NEX) of each scheme. Diffusion data were pre-processed using FSL[https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/] to correct for susceptibility-induced distortions, and eddy currents. The region extraction of cortical, subcortical and white-matter used three atlases, “Desikan-Killiany atlas” from FreeSurfer, the “JHU ICBM-DTI-81 white-matter labels atlas” and the “JHU white-matter tractography atlas”. FA and μFA were calculated each of the diffusion encoding patterns. Regions of interest were drawn on each region as described above.

RESULTS AND DISCUSSION:

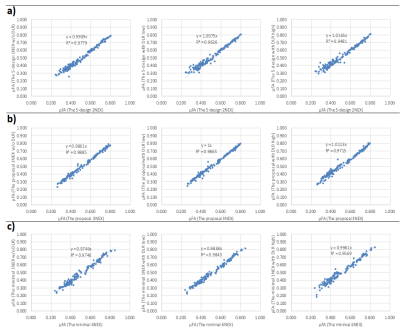
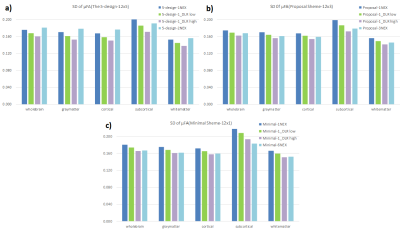
Regarding μFA, the value revealed excellent agreement between each scheme of 1NEX and several NEX, and also revealed excellent agreement between each scheme with and without DLR, regardless of total number of acquisition(Fig.3). The SD value of μFA was decreased by adapting DLR in each scheme, and tended to approach the value of the each several NEX scheme(Fig.4).
Volunteers’ scans demonstrated an increased apparent SNR of each brain segment for μFA image with dDLR(Fig.5). However, the correlation values in Fig. 3 did not differ with or without DLR. This suggests that dDLR does not affect the signal and only the noise part of SD is reduced. Using dDLR can reduce the number of acquisitions, and will contribute to shortening the acquisition time.
In all schemes, to increase the strength of dDLR lowered the correlation value. If the strength of dDLR is increased, the structure itself may be regarded as noise, so it is necessary to appropriately set the strength of dDLR. As this study scanned low resolution, the effect of denoising may be small. In higher resolution imaging conditions, the denoising effect can be expected to be larger.

CONCLUSION:

In this study, the authors adapted the DDE technique and dDLR technique to relevant cases of brain imaging. It was demonstrated that the dDLR techniques are capable of generating DDE with higher SNR compared to normal DDE, with the additional benefit of being able to optimize the acquisition time and number of acquisitions without affecting uFA. While further investigation is necessary, the method of DDE using dDLR is expected to be available in clinical case by reducing acquisition time.

Acknowledgements

No acknowledgement found.