4437
Toolbox for spin-level MRI simulations: an application to cardiac diffusion1Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Institute for Biological and Medical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 4Electrical Engineering Department, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
Cardiac diffusion imaging is a field with multiple challenges to overcome. The main challenge, compared to other techniques, is that the diffusion encoding sequence is prone to artifacts1. In this work, we show the first version of an MRI simulator that includes the most relevant effects for this type of contrast. And could be a useful tool for the development and testing of new pulse sequences. It is programmed in Julia2, which provides an intuitive object-oriented framework for the pulse sequences and creation of digital phantoms. We show two examples with results that correspond well with the theory.
Introduction
Heart micro-structure brings new information about the heart function. Either by explaining the normal state3,4 or the diseased state. As changes in the sheetlet orientation in infarcted zones, and other fiber changes, are associated with ischemia, hypertrophy, and fibrosis1. Most studies have been done in ex-vivo, but the addition of second-order moment-compensation made in-vivo imaging possible5. It is desired that such a simulator should have the following features: (1) Diffusion encoding/micro-structure; (2) Off-resonance effects: fat shift & susceptibility; (3) Non-rigid motion; and (4) Flexible pulse sequence modification. Various simulators have been made6,7,8,9 to develop advanced pulse sequences that target specifically cardiac imaging. However, none of them have all these features.dCMR.jl is a toolbox that simulates the whole acquisition process from a spin perspective. In particular, this toolbox can obtain images that simulate accurately susceptibility and off-resonance effects, different micro-structure characteristics, and moving objects with non-rigid deformations. All of these properties make it ideal for heart microstructure analysis.
Methods
Signal equationThe simulator uses $$$N_{s}$$$ spins with initial position at the $$$n$$$-th spin of $$$\boldsymbol{x}_{n}^{0}$$$. A general expression for the the phase of each individual spin is1,10
$$\phi_{n}\left(\mathbf{x},t\right)=\gamma\int_{0}^{t}(\underbrace{\mathbf{x}_{n}\left(\tau\right)\cdot\mathbf{G}\left(\tau\right)}_{\substack{\text{$k$-space encoding,}\\ \text{including motion}}}+\underbrace{\delta B\left(\boldsymbol{x}_{n}^{0}\right)}_{\text{off-resonance}})\,\mathrm{d}\tau.$$To discretize the problem, the position of each spin was updated as
$$\boldsymbol{x}_{n}\left(t^{k+1}\right)=\boldsymbol{x}_{n}^{0}+\underbrace{\boldsymbol{\eta}\left(\boldsymbol{x}_{n}^{0},t^{k}\right)}_{\text{Diffusion}}+\underbrace{\boldsymbol{u}\left(\boldsymbol{x}_{n}^{0},t^{k}\right)}_{\text{Displacement}},$$
where $$$\boldsymbol{\eta}\left(\boldsymbol{x}_{n}^{0},t^{k}\right)$$$ represents the particle microscopic motion and $$$\boldsymbol{u}\left(\boldsymbol{x}_{n}^{0},t^{k}\right)$$$ is an arbitrary displacement field. The diffusion movement was modeled as a Brownian motion11,12. Which can be represented by a transformation of normally distributed random variables (in 2D)$$\boldsymbol{\eta}\left(\boldsymbol{x}_{n}^{0},t^{k+1}\right)=\boldsymbol{\eta}\left(\boldsymbol{x}_{n}^{0},t^{k}\right)+\mathrm{R}_{z}\left(\theta\left(\boldsymbol{x}_{n}^{0}\right)\right)\left[\begin{array}{c}\sqrt{2\Delta t\lambda_{1}\left(\boldsymbol{x}_{n}^{0}\right)}\xi_{x}\\\sqrt{2\Delta t\lambda_{2}\left(\boldsymbol{x}_{n}^{0}\right)}\xi_{y}\end{array}\right],$$
with $$$\xi_{x},\xi_{y}\sim\mathcal{N}\left(0,1\right)$$$, and $$$\lambda_{1}$$$, $$$\lambda_{2}$$$ and $$$\theta$$$ are maps that describe the object micro-structural properties depending on the initial positions $$$\boldsymbol{x}_{n}^{0}$$$.
In summary, simplifying the notation, the final description of the signal equation is:
$$S\left(t^{k}\right)=\sum_{n=1}^{N_{s}}m_{n}\,\exp\left(-t^{k}/T_{2,n}+i\Delta\omega_{n}t^{k}\right)\exp\left(i2\pi\gamma\Delta t\sum_{l=0}^{k}\boldsymbol{x}_{n}\left(t^{l}\right)\cdot\boldsymbol{G}\left(t^{l}\right)\right),$$
which includes proton density, T2-decay, motion/diffusion and the off-resonance effects.
Toolbox
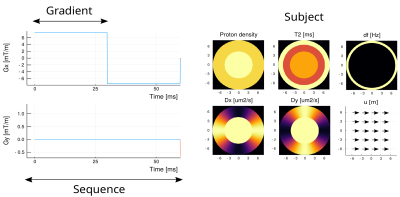
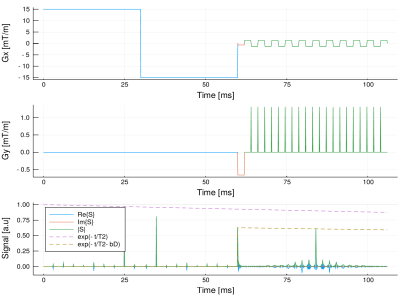
The toolbox was implemented using Julia2, an object oriented programming language. This enables the creation of a framework for high level programming with Gradient objects (defined by its length and strength), the Sequence objects (array of gradients), and the Subject objects (multiple maps as shown in Figure 1). The implementation made possible to set intuitive operations with focus in diffusion imaging. For example, a diffusion encoding sequence with diffusion gradient strength $$$q$$$ and angle $$$\theta$$$ and EPI redout is written with the following actual code line (example in Figure 2): $$\text{SEQ} = q \text{DIFF}\cdot R_z(\theta) + \text{PHASE} + \text{EPI}.$$
Examples
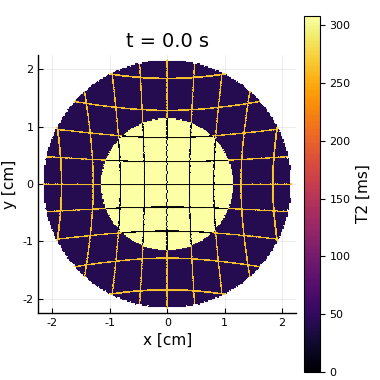
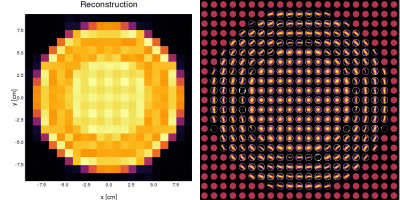
Here we show an example of a pulse sequence with an EPI acquisition and multiple diffusion encoding gradients with 5 different gradient strengths and directions. A $$$b_{\max} = 770.13\text{ s/mm}^2$$$ was set for both, the standard and the moment-compensated diffusion sequence. We used $$$N_s = 25445$$$ spins, $$$N_t=1355$$$ time points, and $$$10$$$ cardiac phases. Static and dynamic ventricle phantoms were used (the latter shown in Video 1). The reconstruction was made in a $$$21\times 21$$$ image by using the inverse Fourier transform of the obtained $$$k$$$-space.
Results
For each DWI the simulation took approximately $$$16$$$ s in a computer with an Intel Core i7-6500U@ 2.5 GHz×4. For the static phantom, we reconstructed images for each of the $$$25$$$th diffusion encodings. Then, we fit the diffusion propagators13 per voxel shown in Video 2. The propagators and images correspond to what is expected.For the dynamic phantom, we reconstructed 10 cardiac phases for $$$\boldsymbol{b}=b_{\max}\hat{\boldsymbol{n}}_x$$$. We see in Video 3 that the higher moments corrupts the image obtained with the PGSE, while the effect is mostly fixed when we include the second-order moment-nulling.
Discussion and conclusion
The simulator lets us verify the effects of non-rigid movements present on the heart and many other parameters ignored by different simulators. Also, we developed a toolbox in which we can quickly generate arbitrary pulse sequences and phantoms with the use of object-oriented programming. The results match the theory, and the resulting images gave expected results so that the simulator could be useful for CMR pulse sequence development or Magnetic Resonance Fingerprinting on the heart. Further research must be done to implement parallel computing and more realistic restricted diffusion models.Acknowledgements
The Millennium Nucleus for Cardiovascular Magnetic Resonance is supported by the Millennium Scientific Initiative of the Ministry of Economy, Development and Tourism (Chile).References
1. Irvin Teh. Cardiac Diffusion MRI. In Christakis Constantinides, editor, Protocols and Methodologies in Basic Science andClinical Cardiac MRI, pages 55–109. Springer International Publishing, Cham, 2018.
2. Jeff Bezanson, Alan Edelman, Stefan Karpinski, and Viral B Shah. Julia: A fresh approach to numerical computing. SIAMreview, 59(1):65–98, 2017.
3. Sonia Nielles-Vallespin, Zohya Khalique, Pedro F. Ferreira, Ranil de Silva, Andrew D. Scott, Philip Kilner, Laura-AnnMcGill, Archontis Giannakidis, Peter D. Gatehouse, Daniel Ennis, Eric Aliotta, Majid Al-Khalil, Peter Kellman, DumitruMazilu, Robert S. Balaban, David N. Firmin, Andrew E. Arai, and Dudley J. Pennell. Assessment of Myocardial Microstruc-tural Dynamics by In Vivo Diffusion Tensor Cardiac Magnetic Resonance. Journal of the American College of Cardiology,69(6):661–676, February 2017.
4. Patrick W. Hales, Jürgen E. Schneider, Rebecca A. B. Burton, Benjamin J. Wright, Christian Bollensdorff, and PeterKohl. Histo-anatomical structure of the living isolated rat heart in two contraction states assessed by diffusion tensor MRI.Progress in Biophysics and Molecular Biology, 110(2):319–330, October 2012.
5. Christian T. Stoeck, Constantin von Deuster, Martin Genet, David Atkinson, and Sebastian Koz-erke. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart.https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.25784, April 2016.
6. Investigation of the XCAT phantom as a validation tool in cardiac MRI tracking algorithms - ScienceDirect.https://www.sciencedirect.com/science/article/pii/S112017971730635X.
7. MCAT to XCAT: The Evolution of 4D Computerized Phantoms for Imaging Research.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4603876/.
8. Lukas Wissmann, Claudio Santelli, William P. Segars, and Sebastian Kozerke. MRXCAT: Realistic numerical phantoms forcardiovascular magnetic resonance. Journal of Cardiovascular Magnetic Resonance, 16(1):63, August 2014.
9. F. Liu, J. V. Velikina, W. F. Block, R. Kijowski, and A. A. Samsonov. Fast Realistic MRI Simulations Based on GeneralizedMulti-Pool Exchange Tissue Model. IEEE Transactions on Medical Imaging, 36(2):527–537, February 2017.
10. Chun-Hung Yeh, Benoît Schmitt, Denis Le Bihan, Jing-Rebecca Li-Schlittgen, Ching-Po Lin, and Cyril Poupon. DiffusionMicroscopist Simulator: A General Monte Carlo Simulation System for Diffusion Magnetic Resonance Imaging. PLoS ONE,8(10):e76626, October 2013.
11. E. O. Stejskal and J. E. Tanner. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent FieldGradient. The Journal of Chemical Physics, 42(1):288–292, January 1965.
12. J. E. Tanner and E. O. Stejskal. Restricted Self-Diffusion of Protons in Colloidal Systems by the Pulsed-Gradient, Spin-EchoMethod. The Journal of Chemical Physics, 49(4):1768–1777, August 1968.
13. Jelle Veraart, Jan Sijbers, Stefan Sunaert, Alexander Leemans, and Ben Jeurissen. Weighted linear least squares estimationof diffusion MRI parameters: Strengths, limitations, and pitfalls. NeuroImage, 81:335–346, November 2013.
Figures