4433
A simulation study of the robustness of cell size and volume mapping for tissue with two underlying cell populations using diffusion weighted MRI
Shu Xing1,2 and Ives R. Levesque1,2,3,4
1Department of Physics, McGill University, Montreal, QC, Canada, 2Medical Physics Unit, McGill University, Montreal, QC, Canada, 3McGill University Health Center Research Institute, Montreal, QC, Canada, 4Department of Oncology, McGill University, Montreal, QC, Canada
1Department of Physics, McGill University, Montreal, QC, Canada, 2Medical Physics Unit, McGill University, Montreal, QC, Canada, 3McGill University Health Center Research Institute, Montreal, QC, Canada, 4Department of Oncology, McGill University, Montreal, QC, Canada
Synopsis
Advanced diffusion-weighted MRI allows non-invasive cell size and volume mapping in cancerous tumours. Existing methods assume that a given voxel contains one cell population. This work investigates the feasibility of estimating the radii and volume fractions of 2 cell populations co-existing in the same voxel and introduces techniques to improve the robustness and stability of fitting. The influence of noise on the fitted parameters is also examined for a range of SNR values. Reliable estimation of cell size and volume for tissue with 2 cell populations opens exciting avenue of potential applications in both tumor diagnosis and treatment monitoring.
Introduction
Cancerous tumours are characterized by their cellular composition and cell size, both linked to tumour type and grade. Advanced diffusion MRI methods have been proposed to map the average cancer cell radius $$$R$$$ and the relative cell volume fraction $$$v_{in}$$$ covering the entire tumour volume(1,2). Existing methods assume that tumours feature a single cell population, which is not valid in many applications. We have previously proposed a two-cell population microstructure model (2P-MM) that can map $$$Rs$$$ and $$$v_{in}s$$$, when 2 cell populations of different radii and volume co-exist in the same voxel(3). Here, we further study the robustness of the 2P-MM under the influence of noise and investigate methods to improve the stability of parameter estimation. The ability to reliably estimate $$$Rs$$$ and $$$v_{in}s$$$ for tissue with 2 cell populations opens exciting avenue of potential applications in tumor diagnosis and treatment monitoring. For instance, round cell/myxoid liposarcoma is composed of high-grade cells (R~10μm) and low-grade cells (R~4μm). The amount of the high-grade component is strongly related to tumor grade and changes the course of treatment (4). The 2P-MM could also potentially quantify the infiltrating T-cells (R~4μm) to cancer cells (R~10μm) during immunotherapy (5).Theory
The normalized diffusion signal of a single cell population is modeled with the one cell population microstructure model (1P-MM):$$ S/S_0=\boldsymbol{v_{in}}S_{in}(\boldsymbol{R,D_{in}})+(1-v_{in})S_{exo}(\boldsymbol{D_{exo}}) \hspace{0.5cm}[1]$$
where Sin and Sexo describe the intracellular restricted diffusion and extracellular hindered diffusion signal, respectively (6). Equation 1 can be extended to a 2P-MM by including an additional restricted diffusion compartment:$$S/S_0=\boldsymbol{v_{in,l}}S_{in,l}(\boldsymbol{R_l,D_{in}})+\boldsymbol{v_{in,s}}S_{in,s}(\boldsymbol{R_s},D_{in})+(1-v_{in,l}-v_{in,s})S_{exo}(\boldsymbol{D_{exo}}) \hspace{0.5cm}[2]$$
where the subscript $$$l$$$ and $$$s$$$ present large and small cell populations. Instead of four fitting parameters (bolded) in Eq. 1, the 2P-MM has six fitting parameters. Stabilization of the fitting quickly becomes the primary challenge. Here, we propose two techniques to reduce the number of fitting parameters, thus stabilizing the fit.
Stabilization by signal suppression from one cell population: special case scenario
The diffusion signals over a range of effective diffusion times Δeff show strong dependence on cell radius (Figure 1). Signal from cells of R=1,2 μm shows little change with Δeff. The Δeff range can be strategically selected to remove signal sensitivity to small cells, where $$$S_{in,s}\approx 1$$$. Eq. 2 is then simplified to:
$$S/S_0=\boldsymbol{v_{in,s}}\cdot1 +\boldsymbol{v_{in,l}}S_{in,l}(\boldsymbol{R_l,D_{in}})+(1-v_{in,l}-v_{in,s})S_{exo}(\boldsymbol{D_{exo}}) \hspace{0.5cm}[3]$$
Stabilization by fixing fitting parameters: general case scenario
- 2-step fitting
- Fixed Din
Method
The matrix method (9) was used to simulate PGSE diffusion signal for a two-cell population input with different $$$Rs$$$ and $$$v_{in}s$$$, using Din = 1μm2/ms and Dexo = 2μm2/ms. Both 1P-MM and 2P-MM were fitted to the simulated signal with 100 starting points. Estimated $$$Rs$$$ and $$$v_{in}s$$$ were compared to ground truth values specified in the simulation. This process was repeated for a range of simulation parameters. Rician noise was added to yield SNR of 20, 50, 80 in the b = 0 ms/μm2 signal and the same fitting process was repeated for 1500 noisy signals. Fits that were not within 1% of the fit constraints were considered acceptable fits.Results and Discussion
The 2P-MM accurately separated the large and small cells for the noiseless fits over a range of radii and volume fractions in both the special and general case (Figure 2). With added noise, the precision of the fitted parameters improved as SNR increased for both scenarios (Figure 3). In this work, interquartile ranges of 2 μm for the fitted Rs and 25% for fitted $$$v_{in}s$$$ were considered acceptable. Thus, a SNR of 50 is required for reliable parameter estimation. Fixing fitting parameters, with the 2-step fitting or fixed Din, generally improved robustness and accuracy (Figure 4). Both techniques produced higher number of acceptable fits and lower median % error on the fitted parameters, with the exception of $$$R_s$$$. The choice of fixed Din values had a noticeable effect on the accuracy of fitted parameters (Figure 5). The fixed Din had to be close to or greater than the true value for the fitted $$$Rs$$$ and $$$v_{in}s$$$ to remain within $$$\pm 1\mu m$$$ and $$$\pm 10\%$$$ of the ground truth. These observations are consistent with prior studies that a relatively large fixed can provide robust fitting with an acceptable sacrifice in accuracy (7,8).Conclusion
In this work, we studied the robustness of the 2P-MM under the influence of noise and proposed methods to improve the stability of the fitting, where microstructure parameters $$$R_l,R_s,v_{in,l}$$$ and $$$v_{in,s}$$$ can be reliably estimated when two cell populations co-exist in the same voxel. This method could be useful in studying biphasic tumours like round cell/myxoid liposarcoma and for treatment monitoring.Acknowledgements
The authors acknowledge Dr. Junzhong Xu, Dr. Xiaoyu Jiang, Zaki Ahmed, and Véronique Fortier for valuable discussions. This work is supported by Medical Physics Research Training Network Grant of the Natural sciences and Engineering Research Council (Grant number: 432290), and the Fonds de Recherche en Santé du Quebec.References
- Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magn Reson Med.2016 Mar;75(3):1076–85.
- Panagiotaki E, Chan RW, Dikaios N, Ahmed HU, Atkinson D, Punwani S, et al. Microstructural Characterisation of Normal and Malignant Human Prostate Tissue with VERDICT MRI. 2014;3:46410.
- Xing S, Levesque IR. Modeling the microstructure of tissue with two cell populations of different sizes using diffusion-weighted MRI. ISMRM. 2019;3540.
- Strander H, Turesson I, Cavallin-StaE. A Systematic Overview of Radiation Therapy Effects in Soft Tissue Sarcomas. Acta Oncol (Madr) 2003;426(5):516–31.
- Chapelin F, Capitini CM, Ahrens ET. Fluorine-19 MRI for detection and quantification of immune cell therapy for cancer. J Immunother Cancer 2018 Dec 11 ;6(1):105.
- Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magn Reson Med 2016 Mar 1;75(3):1076–85.
- Xu J, Jiang X, Li H, Arlinghaus LR, Mckinley ET, Devan SP, et al. Magnetic resonance imaging of mean cell size in human breast tumors
- McHugh DJ, Hubbard Cristinacce PL, Naish JH, Parker GJM. Towards a ‘resolution limit’ for DW-MRI tumor microstructural models: A simulation study investigating the feasibility of distinguishing between microstructural changes. Magn Reson Med 2018 Oct 19
- Ianu AS. Advanced Diffusion MRI for Microstructure Imaging : Theoretical Developments. 2016.
Figures
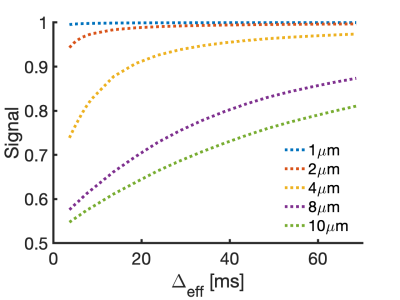
Figure 1 Simulated diffusion signals over a range of diffusion times Δeff show strong dependence on cell radii. Signal from cells of small radii (e.g. 1-2 µm) shows little change over diffusion times. For the 2- cell population model, strategic selection of diffusion times removes signal sensitivity to small cells and reduces the number of fitting parameters, producing more stable fits.
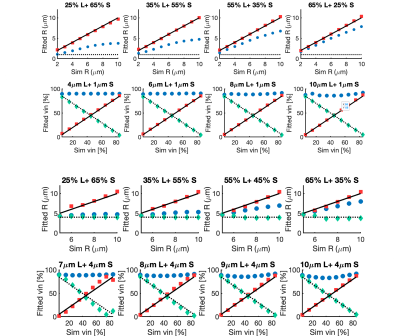
Figure 2 The diffusion signal of different combination of large (L) and small (S) cells are simulated and fitted with both 1P-MM (1P fit) and the 2P-MM in both special and general case scenarios. vin,tot is kept at 90%. Rl (red square) and Rs (green diamond) follows the ground truth closely, whereas the fitted radius from the 1P fit (blue dots) falls between Rl and Rs. vin,l and vin,s also follow the ground truths closely. The 1P fit tends to detect vin,tot occupied by cells (blue dots).
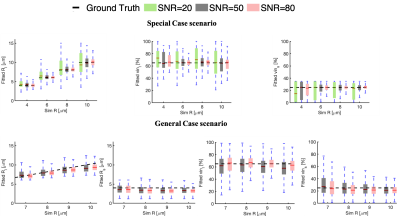
Figure 3 Simulated influence of noise on fitted radii and the volume fractions for both the special (SNR = 20, 50 and 80) and general case scenario (SNR = 50 and 80) is demonstrated. The dotted black lines represent the ground truth. On each box, the central mark indicates the median and the bottom and top edges of the box indicates the 25th and 75th percentiles, respectively.
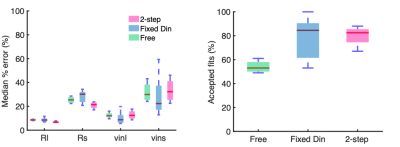
Figure 4 The accuracy and robustness of 3 fitting techniques – leaving all parameters free, 2-step fitting and fitting with fixed Din is evaluated. The median % error of fitted parameters (a) decreases in both the 2-step fitting and fixed Din, with the exception of Rs. Both the 2-step fitting and fitting with fixed Din produce higher number of acceptable fits (b). Fits that are not within 1% of the fit constraints are considered acceptable fits.
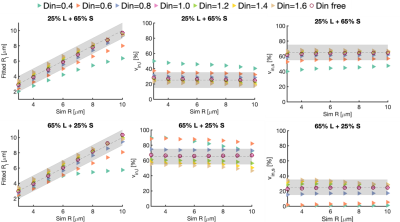
Figure 5 The influence of fixed intracellular diffusion coefficient Din (0.4 – 1.6 μm2/ms ) in the 2P-MM on fitted radii and relative volume fractions is investigated, for ground truth inputs of 25% large cells + 65% small cells (top row) and 65% large cells + 25% small cells (bottom row).