4430

Discrepancy between In-vivo Measurements and Monte-Carlo Simulations with Spherical Structures in B-tensor Encoding
Noemi G Gyori1,2, Matt G Hall2, Christopher A Clark2, Daniel C Alexander1, and Enrico Kaden1
1Centre for Medical Image Computing, University College London, London, United Kingdom, 2Great Ormond Street Institute of Child Health, University College London, London, United Kingdom

Synopsis

In in-vivo B-tensor encoding measurements, linear tensor encoding (LTE) and spherical tensor encoding (STE) waveforms estimate the same mean diffusivity in brain white and grey matter. Contrary to this, we show that in Monte-Carlo simulations of quasi-spherical restrictions, LTE and STE signal decay curves are markedly different and lead to different mean diffusivity estimates. We investigate this discrepancy in the presence of variable compartment sizes, geometric distortions in cell shapes, permeable cell membranes, and water exchange between connected cellular geometries. Our results suggest that a strict model of restricted diffusion may not be suitable for brain tissue.

Introduction

B-tensor encoding is an emerging tool for in-vivo microstructural imaging in the brain. By combining diffusion-weighted measurements that are sensitive to different microscopic tissue features1-5, it has shown promise in reducing degeneracy inherent in the estimation of microscopic tissue parameters6,7, in fitting more complex biophysical models8, and in extracting model-free tissue metrics based on signal representations2,4,5.

In this work, we study the effect of cellular restriction on B-tensor encoding measurements. We use Monte-Carlo simulations to show that within spherical compartments, the diffusion signal is markedly different in linear tensor encoding (LTE) and spherical tensor encoding (STE), contrary to what in-vivo data suggests. We investigate this discrepancy in different cellular configurations.

Methods

In-vivo Data Acquisition
After informed written consent, a healthy volunteer was scanned on a 3T Siemens Prisma scanner using a 64-channel head coil, and a diffusion-weighted EPI sequence that allows measurement with arbitrary gradient waveforms, developed in-house. Isotropic 2 mm voxels were acquired with TE = 96 ms and TR = 9.5 s, at b-values of [0, 500, 1000, 1500, 2000] s/mm2 for both LTE and STE. STE was designed using Maxwell-compensated optimisation9,10 and LTE was made using symmetric trapezoidal pulses. Each waveform was rotated in 32 uniformly distributed gradient directions over the 4 b-shells11.

Monte-Carlo Simulations
We performed Monte-Carlo simulations using Camino12,13 with the same LTE and STE waveforms as in our in-vivo measurements. The gradient amplitudes were adjusted to achieve b-values of [0, 250, 500, 750, 1000, 1250, 1500, 1750, 2000] s/mm2, and each waveform was rotated in 25 uniformly distributed directions. All simulations used 1,000 time steps and 100,000 random walkers with intrinsic diffusivity set to 2 μm2/ms. Substrates consisted of custom meshes placed in a simulation box with periodic boundary conditions.

Results and Discussion

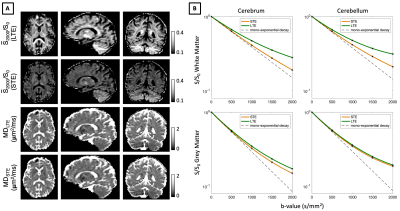
B-tensor Encoding In-vivo
Figure 1 shows in-vivo B-tensor encoding data in the human brain. The initial slope of signal decay curves, associated with mean diffusivity (MD), converges for LTE and STE including in grey matter regions that contain small cellular structures such as neural soma. Using low b-values of 500 s/mm2, we map MD estimated from both LTE and STE measurements, and show that these are indeed very similar.

Monte-Carlo Simulations of B-tensor Encoding
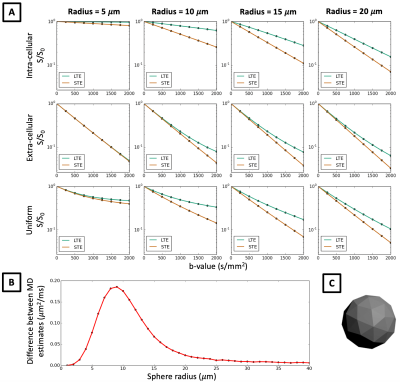
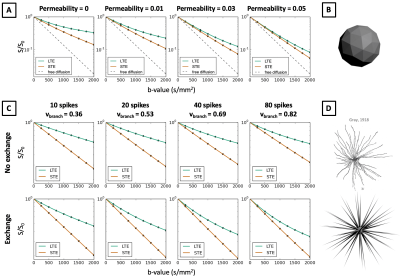
In Figure 2 we show that in quasi-spherical compartments with constant sizes, Monte-Carlo simulations of LTE and STE measurements are markedly different, contrary to what in-vivo data suggests. Within spherical meshes, signal decay is largely mono-exponential, but LTE and STE have different slopes, and hence estimate different MD in the same sample. The largest difference between MD estimates occurs between 5-20 μm sphere radii, which is within the biophysically plausible range of neural soma sizes. This effect cannot be observed in extra-cellular space where signal decay curves converge for small b-values, which suggests that differences in MD between LTE and STE are mainly due to cellular restriction. These results are contrary to our observations in in-vivo data and suggest that B-tensor encoding is highly sensitive to restriction. When random walkers are uniformly distributed in the simulation substrate, such that the intra-cellular volume fraction (vintra) is 0.52, signal decay curves misleadingly suggest that there is significant compartment anisotropy in the sample. In addition to higher order effects shown in Ref. 14, we demonstrate that in spherical compartments, diffusion-weighting waveforms have a first order effect on the signal with respect to the b-value.

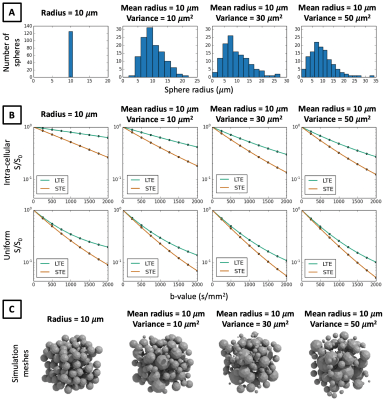
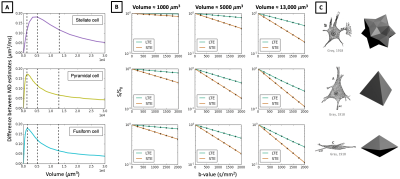
In Figures 3-5 we investigate different cellular configurations that may bring Monte-Carlo simulations closer to in-vivo observations. Firstly, we use simulation substrates with variable sphere sizes drawn from a gamma distribution. Figure 3 shows that there is a large discrepancy between LTE and STE signals even for a wide distribution of spherical compartment sizes. In Figure 4 we investigate different cell shapes and show that MD estimated from LTE and STE does not converge, despite geometrical distortions in cell shapes. Finally, we study exchange processes. Figure 5A demonstrates that as the permeability of spherical compartments is increased, LTE and STE signal decay curves do indeed converge in the low b-value regime. Meanwhile, Figure 5C demonstrates the effect of water exchange between connected quasi-spherical structures (e.g. cell bodies) and quasi-cylindrical structures (e.g. cell projections), using meshes similar to Ref. 15. Water exchange between these compartments has a significant effect on the signals, and for a large number of projections mean diffusivity measured by LTE and STE converges, similarly to in-vivo signal profiles. These results suggest that exchange processes are a possible reason why a simple model containing spherical restrictions does not match B-tensor encoding measurements.

Conclusion

In this work, we demonstrate that in Monte-Carlo simulations of isotropic compartments with no size variance, LTE and STE B-tensor encoding measurements are strikingly different and give rise to different mean diffusivity estimates. This contradicts in-vivo observations, where LTE and STE signals converge at low b-values. We study different cellular configurations that may reduce the discrepancy between in-vivo measurements and simulations, including cell size variation, geometrical distortions in cell shapes, cellular permeability, and water exchange processes between connected compartments of different geometries. Our results suggest that a strict model of cellular restriction may not be suitable for brain tissue.

Acknowledgements

NGG thanks the London Interdisciplinary Bioscience PhD Consortium. This research was funded by UK BBSRC BB/M009513/1, EPSRC EP/M020533/1, EP/N018702/1 and EU H2020 634541-2, and was supported by the UK NIHR Great Ormond Street Hospital Biomedical Research Centre and NIHR UCLH Biomedical Research Centre.

References

[1] Eriksson, S., Lasic, S., Topgaard, D. (2013) Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. Journal of Magnetic Resonance 226, pp. 13–18.

[2] Lasic, S, Szczepankiewicz, F., Eriksson, S., Nilsson, M., Topgaard, D. (2014) Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics 2.11, pp. 1–14.

[3] Eriksson, S., Lasic, S., Nilsson, M., Westin, C.-F., Topgaard, D. (2015) NMR diffusion encoding with axial symmetry and variable anisotropy: distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of Chemical Physics 142.10, p. 104201.

[4] Westin, C.-F., Knutsson, H., Pasternak, O., Szczepankiewicz, F., Ozarslan, E., van Westen, D., Mattisson, C., Bogren, M., O’Donnell, L. J., Kubicki, M., Topgaard, D., Nilsson, M. (2016) Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 135, pp. 342–362.

[5] Topgaard, D. (2017) Multidimensional diffusion MRI. Journal of Magnetic Resonance 275, pp. 98–113.

[6] Reisert, M., Kiselev, V. G., Dhital, B. (2019) A unique analytical solution of the white matter standard model using linear and planar encodings. Magnetic Resonance in Medicine 81.6, pp. 3819-3826.

[7] Coelho, S., Pozo, J. M., Jespersen, S. N., Jones, D. K., Frangi, A. F. (2019) Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding. Magnetic Resonance in Medicine 82.1, pp. 395-410.

[8] Gyori, N. G., Clark, C. A., Dragonu, I., Alexander, D. C., Kaden, E. (2019) In-vivo neural soma imaging using B-tensor encoding and deep learning. In Proceedings of the ISMRM, #0059.

[9] Sjolund, J., Szczepankiewicz, F., Nilsson, M., Topgaard, D., Westin, C.-F., Knutsson, H. (2015) Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance 261, pp. 157–168.

[10] Szczepankiewicz, F., Westin, C.-F., Nilsson, M. (2019) Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magnetic Resonance in Medicine 82.4, pp. 1424–1437.

[11] Caruyer, E., Lenglet, C., Sapiro, G., Deriche, R. (2013) Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine 69.6, pp. 1534-1540.

[12] Cook, P. A., Bai, Y., Nedjati-Gilani, S., Seunarine, K. K., Hall, M. G., Parker, G. J., Alexander, D. C. (2006) Camino: open-source diffusion-MRI reconstruction and processing. In Proceedings of the ISMRM, #2759.

[13] Hall, M. G., Alexander, D. C. (2008) Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE Transactions on Medical Imaging, pp. 1354–1364.

[14] Lundell, H., Nilsson, M., Dyrby, T. B., Parker, G. J., Hubbard Cristinacce, P. L., Zhou, F.-L., Topgaard, D., Lasic, S. (2019) Multidimensional diffusion MRI with spectrally modulated gradients reveals unprecedented microstructural detail. Scientific Reports 9.1, p. 9026.

[15] Palombo, M., Ianus, A., Nunes, D., Guerreri, M., Alexander, D. C., Shemesh, N., Zhang, H. (2019) SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. ArXiv: 1907.02832.

[16] Gray, H. (1918) Anatomy of the Human Body. Philadelphia: Lea and Febiger.

Figures

Figure 1. In-vivo data acquired with LTE and STE waveforms. (A) T2-normalised maps at b-value of 2000 s/mm2 show that at high b-values LTE and STE measure different contrast in the brain. Nonetheless, the mean diffusivity estimated from the lowest measured b-value, 500 s/mm2, appears to be similar for LTE and STE. (B) Signal decay in different regions of the brain shows that LTE and STE have similar initial slopes, associated with mean diffusivity, and diverge only at higher b-values.

Figure 2. (A) LTE and STE simulations measure different diffusion signals in spherical meshes with constant sizes (panel C). Within spheres, signal decay with respect to the b-value appears mono-exponential, but contrary to in-vivo data, LTE and STE estimate different MD. Panel B shows that this is most pronounced in sphere radii of 5-20 μm, which are biophysically plausible soma sizes. This effect cannot be seen in extra-cellular diffusion. In uniform placement of random walkers (vintra = 0.52), signal decay curves misleadingly suggest significant compartment anisotropy.

Figure 3. LTE and STE signals when spherical compartments have different size distributions. (A) Histograms of 125 sphere sizes drawn from a gamma distribution for mean radius of 10 μm and different variances. (B) Signal decay in LTE and STE when random walkers are placed inside the spherical meshes, and when they are placed uniformly inside and outside the spheres (vintra = 0.3). Within spheres, the initial slope of LTE and STE curves are different despite size variance. (C) Simulation meshes for different size distributions.

Figure 4. Intra-cellular signal decay for different soma shapes, such as stellate, pyramidal and fusiform cells. (A) The difference between LTE and STE mean diffusivity estimates for the different cell shapes. In anisotropic cells, differences between the signals occur at smaller volumes than in more isotropic cells. (B) LTE and STE signal decay curves are largely mono-exponential even within anisotropic cell shapes. This suggests that it may be difficult to disentangle smaller, slightly anisotropic cells from bigger, isotropic cells. (C) Simulation meshes inspired by Ref. 16.

Figure 5. (A) Mean diffusivity measured by LTE and STE for increasingly permeable spheres of radius = 10 μm (panel B). Random walkers are placed uniformly in the substrate where vintra = 0.52, and permeability is the probability for a walker to cross the mesh. (C) Signal decay in spider cells (panel D) with and without water exchange between quasi-spherical and quasi-cylindrical structures. Water exchange has a significant effect on the signals, and for a large number of projections, mean diffusivity measured by LTE and STE converges, similarly to in-vivo signal profiles.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
4430