4429
Indetermination-free cytoarchitecture measurements in brain gray matter via a forward diffusion MRI signal separation method1Université Paris-Saclay, Inria, CEA, Palaiseau, France
Synopsis
Non-invasive imaging at the cellular level could lead us to quantify grey matter tissue cytoarchitecture, which has so far been accessible only through histology, or by indeterminate-prone approaches.
We propose a new dMRI-based index to study modulated by the size of the somas. This index can be extracted without indeterminations from any acquisition including three b-values superior to 3 ms/μm2. Simulations were experimentally confirmed by tests on the HCP MGH data set.
Introduction
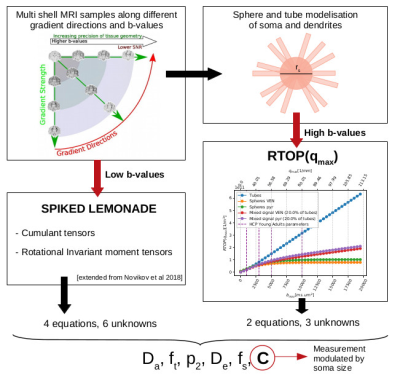
In this work we solve the problem of estimating soma sizes in grey matter with no indetermination. To extract a soma size-modulated mesasurement, we combine approximations to a biophysical model at low b-values and its associated return-to-the-origin probability (RTOP)1 for high b-values.Such non-invasive measurement of cellular characteristics has the potential to quantify tissue cytoarchitecture, in a unique-solution system, which has so far been accessible only through histology.
Our contribution focuses on the human brain gray matter, which can be decomposed into three compartments, somas and processes that are modeled by spheres and 0-radius tubes, and extra-cellular water. This work shows the feasibility to extract factor that reflects the averaged diameter of the somas in the voxel with a unique solution. Our three-compartment model, under the hypothesis that there is no exchange between the three compartments2, is as follow :
\begin{equation} \frac{S(q)}{S(0)} = f_{t}S_{tubes}(q, D_a) + f_{s}S_{spheres}(q, D_{s}, r_{s}) + (1 - f_{t} - f_{s}) S_{ecs}(q, D_{ecs})\end{equation}
ft and fs represent the MR dendrite and soma signal fraction respectively, Decs and Ds the extra-cellular and soma diffusivities, Da axial diffusivity and rs the soma radius.
The tube signal is modeled by a power-law scaling3 $$$\frac{1}{4 \sqrt{\pi \tau D_a^{||}}} \cdot q^{-1} + \gamma $$$, and the sphere signal by Balinov's approximation4 $$$-\log S_{spheres}(q) = C(r_{s}, D_{s}) \cdot q^2$$$. Here we exploit this relation to extract $$$C = C(r_{s}, D_{s})$$$ that, at fixed $$$D_s$$$, modulated by soma size with a method that can be applied to acquisitions with just 5 b-values. Three of them must be superior to a minimum b-value defined by cell soma size, see Fig2. The spacing of these points is determined by the SNR as the signal difference between points must not be noise-dominated.
Others5 have already propose solutions to dMRI soma measurement for high b-values, and more b-values in all, but their method leads to indeterminate systems. Our direct method is indetermination free.
Methods
By combining the expression to our biophysical model (1) for RTOP at large q (respectively b) and a Lemonade variant at low b (respectively q), we produce a method to extract the parameters of our model.RTOP: high b. We compute a q-bounded RTOP, a direct measure of the restrictions of the diffusing fluid molecule motion that gives us information about the structure of the media6,7:
\begin{equation} RTOP(q_{max}) = \frac{1}{(2\pi)^{3}} \int_{0}^{q_{max}}{\frac{S(q)}{S(0)}} dq_{max}\end{equation}
For qmax large enough, RTOP of the sphere signal converges towards a value that depends on C. We therefore obtain from eqs (1) and (2) assuming a large enough qmax :
\begin{equation} RTOP(q_{max}) = \frac{(1 - f_{t})}{(2\pi)^2 \cdot 8 \sqrt{\pi} \cdot 4 C^{3/2}} + \frac{f_{t}}{4(2\pi)^3\sqrt{\pi \tau D_a^{||}}} \cdot q_{max}^2 + \frac{\gamma}{3(2 \pi)^{3}} \cdot q_{max}^3\end{equation}
By solving an ordinary least square regression we can find the coefficients afit, bfit and cfit of the previous polynomial and we end up with 2 equations with 3 unknowns.
Spiked LEMONADE: low b. We adapted the method proposed in 8 in adding the sphere contribution (fs and C). Estimating the rotational invariant moment tensors M(2),0, M(2),2, and M(4),2 for a b-value up to 2.5ms/μm2 we can find 4 more equations with 6 unknowns.
Total system. We end up with a system of 6 equations for 6 unknowns that has no degeneracy.
Spiked LEMONADE, low b :
\begin{equation} \begin{cases} M^{(2),0} = f_t D_a + 3 \boldsymbol{f_s C} + 3 (1 - f_t - f_s) D_e \\ \frac{M^{(2),2}}{p_2} = f_t D_a \\ M^{(4),0} = f_t D_a^2 + 5 \boldsymbol{f_s C}^2 + 5 (1 - f_t - f_s) D_e^2 \\ \frac{M^{(4),2}}{p_2} = f_t D_a^2 \end{cases} \end{equation}
RTOP, high b:
\begin{equation} \begin{cases} a_{fit} = \frac{(1 - f_{t}) \sqrt{\pi}}{(2\pi)^3 \cdot 4 \boldsymbol{C}^{3/2}} \\ b_{fit} = \frac{f_{t} \sqrt{\pi}}{2(2\pi)^4\sqrt{\tau D_a^{||}}} \end{cases} \end{equation}
Numerical simulations. To mimic neurons, we modelled the sphere and tube signals using the DMIPY simulator7 with soma radius equal to approximately 20 and 15μm, reproducing Von Economo and pyramidal neurons.
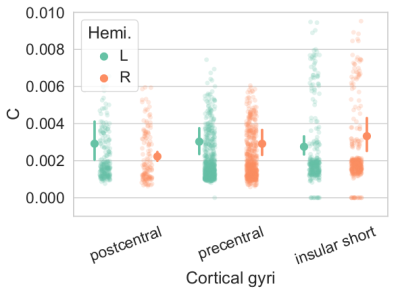
Experimental Data. We used the HCP MGH Adult Diffusion data set to study the variation of C on the insula, precentral and postcentral parts of the Destrieux atlas. It is composed of 35 subjects, with δ/Δ=10.6/43.1ms and b=1, 3, 5, 10ms/μm2.
Results
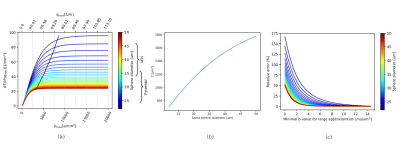
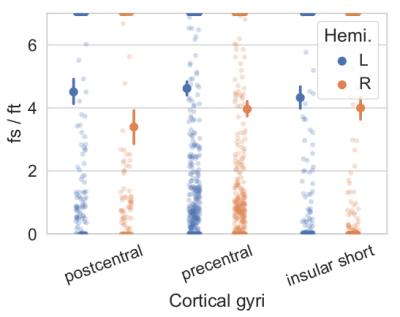
Simulations. RTOP computation on soma simulations shows the convergence values specific to soma diameters of different neurons in the brain, obtained from Neuromorpho.org (Fig.2a). This value is proportional to C, and Fig2b shows that C is modulated by the size of the somas, and inversely proportional to it. The relative error of C with respect to the minimum b-value used for the RTOP computation is presented in Fig2c.Experiments. Fig3, C value for three cortical regions on subject 1010 (right handed), preliminary evidence shows: larger soma size spread and asymmetry on the insula, agreeing with 9. and larger somas on the left postcentral, possibly hemispheric dominance10. Fig 4. Soma-to-dendrite volume ratio showing soma predominance agreeing with literature10. Although further work is needed, this showcases our method’s potential.
Discussion and Conclusion
The minimal b-value needed to compute the large approximation of the signal RTOP must be at least 3ms/μm2 to get a good C approximation in the case of VEN and pyramidal neurons. The proposed method does not need a large range of b-values as in 5.Acknowledgements
This work was supported by the ERC-StG NeuroLang and the ANR/NSF NeuroRef grants.References
1. Partha P. Mitra and Pabitra N. Sen. Effects of microgeometry and surface relaxation onNMR pulsed-field-gradient experiments: Simple pore geometries.Physical Review B, 453(1):143–156, January 1992. ISSN 0163-1829, 1095-3795. doi: 10.1103/PhysRevB.45.143.URLhttps://link.aps.org/doi/10.1103/PhysRevB.45.143.
2. Palombo M, Shemesh N, Ianus A, et al., Abundance of cell bodies can explain the stickmodel’s failure to describe high b-value diffusion signal in grey matter. Proc. Int. Soc.Magn. Reson. Med. 2018, 1096
3. Jelle Veraart, Els Fieremans, and Dmitry S. Novikov. On the scaling behav-ior of water diffusion in human brain white matter.NeuroImage, 185:379–387,January 2019. ISSN 10538119. doi: 10.1016/j.neuroimage.2018.09.075. URLhttps://linkinghub.elsevier.com/retrieve/pii/S1053811918319475
4. Balinov et al. The NMR Self-Diffusion Method Applied to Restricted Diffusion. Simu-lation of Echo Attenuation form Molecules in Spheres and between Planes. 1993
5. Marco Palombo, Clemence Ligneul, and Julien Valette. Modeling diffusion of intracel-lular metabolites in the mouse brain up to very high diffusion-weighting: Diffusion inlong fibers (almost) accounts for non-monoexponential attenuation: Modeling Diffusionof Brain Metabolites in Vivo up to Very High Diffusion Weighting.Magnetic Resonancein Medicine, 77(1):343–350, January 2017. ISSN 07403194. doi: 10.1002/mrm.26548.URLhttp://doi.wiley.com/10.1002/mrm.26548
6. Rutger H.J. Fick, Demian Wassermann, Emmanuel Caruyer, and Rachid De-riche.MAPL: Tissue microstructure estimation using Laplacian-regularizedMAP-MRI and its application to HCP data.NeuroImage, 134:365–385,July 2016. ISSN 10538119. doi: 10.1016/j.neuroimage.2016.03.046. URLhttps://linkinghub.elsevier.com/retrieve/pii/S1053811916002512
7. Mitra et al. Pulsed-field-gradient NMR measurements of restricted diffusion and thereturn-to-origin probability.Journal of Magnetic Resonance, 114:47–58, 1995
8. Dmitry S. Novikov, Jelle Veraart, Ileana O. Jelescu, and Els Fieremans. Rotationally-invariant mapping of scalar and orientational metrics of neu-ronal microstructure with diffusion MRI.NeuroImage, 174:518–538, July2018.ISSN 10538119.doi: 10.1016/j.neuroimage.2018.03.006.URLhttps://linkinghub.elsevier.com/retrieve/pii/S1053811918301915
9. Evrard, H. C., Forro, T. & Logothetis, N. K. Von Economo Neurons in the Anterior Insula of the Macaque Monkey. Neuron 74, 482–489 (2012)
10. Katrin Amunts and Karl Zilles.Architectonic Mapping of the Hu-man Brain beyond Brodmann.Neuron, 88(6):1086–1107, Decem-ber 2015.ISSN 08966273.doi: 10.1016/j.neuron.2015.12.001.URLhttps://linkinghub.elsevier.com/retrieve/pii/S0896627315010727
Figures