4421

Data-Driven Multi-Contrast Spectral Microstructure Imaging with InSpect: INtegrated SPECTral Component Estimation and Mapping

Paddy J. Slator¹, Jana Hutter^2,3, Razvan V. Marinescu¹, Marco Palombo¹, Laurence Jackson^2,3, Alison Ho⁴, Lucy C. Chappell⁴, Mary A. Rutherford², Joseph V. Hajnal^2,3, and Daniel C. Alexander¹
¹Centre for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom, ²Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, ³Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, ⁴Women's Health Department, King's College London, London, United Kingdom

Synopsis

We introduce a novel spectroscopic imaging technique - termed InSpect - for analysing multi-contrast microstructural MRI experiments. Such data potentially supports estimation of multidimensional correlation spectra via a regularised inverse Laplace transform, but this is an ill-posed calculation. InSpect addresses these limitations in a data-driven way. The algorithm simultaneously estimates a canonical basis of spectral components for the whole data set, and maps their spatial distribution across images. Unlike standard approaches, InSpect shares information across voxels, implementing data-driven regularisation of the inverse Laplace transform. We demonstrate the method on combined diffusion-relaxometry placental MRI scans, revealing anatomically-relevant substructures, and identifying dysfunctional placentas.

Introduction

Simultaneous multi-contrast MRI is an emerging technique, recently demonstrated in placenta[1,2], and brain[3-8]. By providing information on correlations and couplings between complementary MR properties, this approach can potentially resolve distinct microstructural compartments that are indistinguishable with a single contrast. A regularised inverse Laplace transform (ILT) estimates multidimensional correlation spectra from such data, but is highly ill-posed. Estimating spectra in each image voxel independently therefore requires unrealistically high signal-to-noise (SNR). Moreover, this approach necessitates “spectral integration” - numerical integration of voxelwise spectra within ad-hoc bounded regions[4,5,9] - to obtain spatial maps or statistics.

Here we present a method - termed InSpect - which addresses these limitations in a data-driven way. It simultaneously estimates a canonical basis of spectral components for the whole image (or data set), and the voxelwise weighting factors of each component. This adapts the analogous segmentation algorithm[10] for continuous mapping rather than clustering and categorisation. Unlike the standard ILT approach, InSpect exploits the huge dependence among voxels, dramatically reducing the SNR required for stable inversion. It also provides a natural lower-dimensional representation enabling standard downstream analysis of ROIs without manual division of the spectral domain. We demonstrate InSpect using diffusion-relaxometry placental MRI data.

Methods

InSpect is based on a continuum model, which assumes that single voxels contain spins with a spectrum of MR properties. For T2*-diffusivity multi-contrast MRI the voxel signal is$$S(b,T_E)=\int\int F(T_2^*,ADC)K(b,T_E,T_2^*,ADC)\;dADC\:dT_2^*$$where$$K(b,T_E,T_2^*,ADC)=\exp(-bADC)\exp\left(-\frac{T_E}{T_2^*}\right),$$$$$b$$$ and $$$T_E$$$ are the b-value and echo time, and$$$\:F\:$$$is the T2*-ADC spectrum. The typical approach, following[11-13], discretises the continuous model onto a grid$$S=KF$$and estimates F with a regularised ILT$$F=\underset{F\geq0}{\operatorname{argmin}}\left\lVert KF-S\right\rVert_2^2+\alpha\left\lVert F\right\rVert_2^2.$$Volume fraction maps are then produced by numerically integrating voxelwise spectra over user-defined regions of the spectrum, e.g.[4,5,9].

InSpect automates spectral mapping, and avoids ILT regularisation. Rather than naively fitting spectra to each voxel independently, the algorithm learns a data-driven low-dimensional representation consistent with the whole image. The representation comprises a pre-specified number $$$M$$$ of canonical spectral components, $$$\{F_1,F_2,...,F_M\}$$$, and their corresponding voxelwise weights across all $$$N$$$ image voxels, denoted$$\{z_{n1},z_{n2},...,z_{nM}\}_{n=1}^N,\;\text{subject to}\;\sum_{m=1}^Mz_{nm}=1$$
where$$$\:z_{nm}\:$$$is the weighting of component $$$m$$$ in voxel $$$n$$$. The spectrum in voxel$$$\:n\:$$$is modelled as a weighted sum:$$F(\mathbf{z_n})=\sum_{m=1}^Mz_{nm}F_m$$where $$$\mathbf{z_n}=\{z_{nm}\}_{m=1}^M$$$ are the component weights for voxel$$$\:n$$$. The discretised model is$$S_n=KF(\mathbf{z_n}),\:\text{for voxels}\:n=1,...,N$$and, assuming Gaussian noise, the log-likelihood across all voxels is$$p(S|F_1,...,F_m,\{z_{n1},z_{n2},...,z_{nM}\}_{n=1}^N)=\sum_{n=1}^N\log N(S_n;KF(\mathbf{z_n}),\sigma_n^2).$$The canonical spectral components, $$$F_m$$$, and voxelwise maps, $$$\{z_{n1},z_{n2},...,z_{nM}\}_{n=1}^N$$$, can be estimated by iteratively maximising$$F_m=\underset{{F_m\geq 0}}{\operatorname{argmin}}\left\lVert\sum_{n=1}^N(K z_{nm})F_m-\sum_{n=1}^N\left(S_n-K\left(\sum_{m\neq n}z_{nm}F_m\right)\right)\right\rVert_2^2$$and$$\{z_{nm}\}_{m=1}^M=\underset{{\sum_{m=1}^Mz_{nm}=1}}{\operatorname{argmax}}\log N(S_n;KF(\mathbf{z_n}),\sigma_n^2),\;\text{for voxels}\;n=1,...,N$$with non-negative least squares and interior-point algorithms respectively.

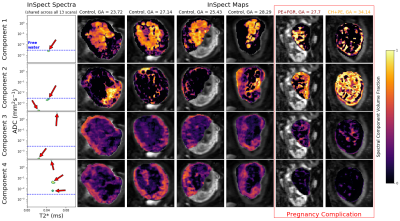
We demonstrate InSpect using previously published placental T2*-diffusion data[2]. The sequence has 66 diffusion-weightings from b=5-1600s/mm², 5 TEs (78, 114, 150, 186, 222ms), FOV=300×320×84mm, TR=7s, SENSE=2.5, halfscan=0.6, resolution=3mm³. We considered 13 scans from 12 participants, containing healthy controls and participants with pregnancy complications (details in Table 1). We fit InSpect - with an exploratory choice of $$$M=4$$$ components - to this multi-participant dataset simultaneously, i.e. fitting to all images jointly, estimating a common set of spectral components across all participants.

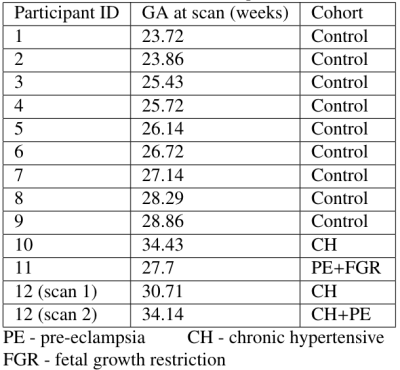
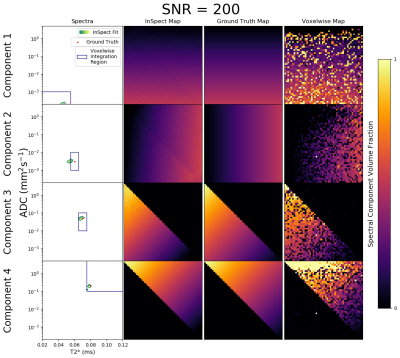
We also tested on simulated diffusion-relaxometry data. Four canonical spectral components - informed by observed placental spectra[2] - and their ground truth voxelwise weights were defined. Given these we simulated diffusion-relaxometry scans as$$S_n(b,T_E)=KF(\mathbf{z_n})=K\left(\sum_{m=1}^Mz_{nm}F_m\right)$$using the same b-values and TEs as the placental dataset, and adding Rician noise. We fit InSpect - specifying $$$M=4$$$ components - to these scans. We also calculated maps by fitting spectra voxelwise then numerically integrating within user-defined regions, e.g.[4,5,9].

Results

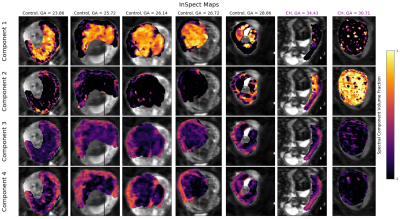
Figures 2 and 3 demonstrate that InSpect outperforms the voxelwise approach on simulated data. It improves estimation of ground truth maps, and accurately recovers spectral components - which require manual identification in the voxelwise approach.

Figures 4 and 5 present the joint InSpect fit to all participants’ placental MRI images. The component-associated maps identify consistent anatomical structures across controls, and show clear differences in dysfunctional placentas.

Discussion

Given spatial patterns and spectrum characteristics in placenta fits, we make initial speculations about the microstructural environment associated with each component.

Component one maps out lobular structures in the placenta, and consists of a single spectral peak with ADC close to free water. These observations indicate that this component may represent maternal blood pools within the placenta.

Component two appears to encircle these lobules, and contains a restricted (i.e. very low ADC) spectral peak. This is consistent with this component representing tissular structures, including the lobule-enclosing septa.

In control participants, components three and four are prominent in the uterine wall. Both component-associated spectra contain peaks with higher ADC than free water, suggesting the presence of perfusing blood. This may be maternal blood in uterine wall areas and fetal blood within the placenta. These components are considerably reduced in dysfunctional placentas, likely indicative of pathology.

In this study, we fit InSpect to 13 scans simultaneously. Other approaches - such as fitting to individual scans - may be preferable depending on the specific application.

Future work will explore how to select$$$\:M$$$, the number of spectral components automatically, e.g. through model selection statistics, cross validation, and/or prior microstructural knowledge.

Conclusion

We present a data-driven approach for multi-contrast MRI data analysis, and demonstrate its ability to quantify placental dysfunction. InSpect exploits within-image redundancies to simultaneously estimate a set of canonical spectral components and their mapping across images, offering significant advantages over typical multidimensional spectrum estimation methods. The approach generalises to applications in many tissue types and imaging modalities.

Acknowledgements

We thank all mothers, midwives, obstetricians, and radiographers who played a key role in obtaining the datasets. This work was supported by the NIH Human Placenta Project grant 1U01HD087202-01 (Placenta Imaging Project [PiP]); Wellcome Trust (201374/Z/16/Z); EPSRC (N018702, M020533, EP/N018702/1); NIHR (RP-2014-05-019); the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and Kings’ College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

1. Melbourne A, Aughwane R, Sokolska M, Owen D, Kendall G, Flouri D, et al. Separating fetal and maternal placenta circulations using multiparametric MRI. Magnetic Resonance in Medicine. John Wiley & Sons, Ltd; 1 Jan 2018: 350–361. doi:10.1002/mrm.27406

2. Slator PJ, Hutter J, Palombo M, Jackson LH, Ho A, Panagiotaki E, et al. Combined Diffusion-Relaxometry MRI to Identify Dysfunction in the Human Placenta. Magn Reson Med. John Wiley & Sons, Ltd; 2019; 1–22. doi:10.1002/mrm.27733

3. De Santis S, Barazany D, Jones DK, Assaf Y. Resolving relaxometry and diffusion properties within the same voxel in the presence of crossing fibres by combining inversion recovery and diffusion-weighted acquisitions. Magn Reson Med. Wiley-Blackwell; 2016;75: 372–380. doi:10.1002/mrm.25644

4. Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion-relaxation correlation spectroscopic imaging: A multidimensional approach for probing microstructure. Magn Reson Med. 2017;78: 2236–2249. doi:10.1002/mrm.26629

5. Benjamini D, Basser PJ. Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments. Neuroimage. Elsevier Inc.; 2017;163: 183–196. doi:10.1016/j.neuroimage.2017.09.033

6. Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage. Elsevier Inc.; 2018;182: 360–369. doi:10.1016/j.neuroimage.2017.09.030

7. Hutter J, Slator PJ, Christiaens D, Teixeira RPAG, Roberts T, Jackson L, et al. Integrated and efficient diffusion-relaxometry using ZEBRA. Sci Rep. Springer US; 2018;8: 15138. doi:10.1038/s41598-018-33463-2

8. Ning L, Gagoski B, Szczepankiewicz F, Westin C-F, Rathi Y. Joint RElaxation-Diffusion Imaging Moments (REDIM) to probe neurite microstructure. IEEE Trans Med Imaging. Institute of Electrical and Electronics Engineers (IEEE); 2019; 1–1. doi:10.1109/tmi.2019.2933982

9. Mackay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. Wiley-Blackwell; 1994;31: 673–677. doi:10.1002/mrm.1910310614

10. Slator PJ, Hutter J, Marinescu R V., Palombo M, Young AL, Jackson LH, et al. InSpect: INtegrated SPECTral Component Estimation and Mapping for Multi-contrast Microstructural MRI. Information Processing in Medical Imaging (IPMI) 2019. Springer, Cham; 2019. pp. 755–766. doi:10.1007/978-3-030-20351-1_59

11. Menon RS, Allen PS. Application of continuous relaxation time distributions to the fitting of data from model systmes and excised tissue. Magn Reson Med. Wiley-Blackwell; 1991;20: 214–227. doi:10.1002/mrm.1910200205

12. English AE, Whittall KP, Joy MLG, Henkelman RM. Quantitative Two-Dimensional time Correlation Relaxometry. Magn Reson Med. John Wiley & Sons, Ltd; 1991;22: 425–434. doi:10.1002/mrm.1910220250

13. Ronen I, Moeller S, Ugurbil K, Kim D-S. Analysis of the distribution of diffusion coefficients in cat brain at 9.4 T using the inverse Laplace transformation. Magn Reson Imaging. Elsevier; 2006;24: 61–68. doi:10.1016/j.mri.2005.10.023

14. Hansen PC. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Rev. 1992;34: 561–580. doi:10.1137/1034115

Figures

Table 1: Participant details, GA – gestational age, PE - pre-eclampsia, CH - chronic hypertensive, FGR - fetal growth restriction.

Figure 2: InSpect model applied to simulated images with SNR=200. The InSpect model fit is presented in columns 1-2: inferred spectral components (green-yellow peaks, column 1), and corresponding voxelwise weights (column 2). Column 3: ground truth voxelwise weights; ground truth spectral components (red dots in column 1) have fixed T2*-ADC values of (0.05, 0.0002), (0.06, 0.003), (0.07, 0.05) and (0.08 ms, 0.2 mm²/s). Column 4: maps obtained by numerical integration (within blue regions of column 1) of voxelwise spectral fits (we set α=0.01 for these fits, following [14]).

Figure 3: As Figure 2, but with lower signal-to-noise ratio (SNR=100) in the simulations.

Figure 4: InSpect model jointly fit to 13 placenta diffusion-relaxometry scans. Each row displays the spectrum (leftmost box, separated spectral peaks highlighted with red arrows) and corresponding volume fraction maps for a single canonical spectral component. Note that the spectra in column 1 are shared across all 13 participants. Columns 2-7 each display a single participants’ maps for 6 of the 13 scans, including two who had been diagnosed with a pregnancy complication at scan time. See Figure 5 for maps from the remaining 7 scans.

Figure 5: InSpect maps for 7 participants from the InSpect model jointly fit to 13 placenta diffusion-relaxometry scans. Each row displays maps for a single canonical spectral component - see first column of Figure 4 for the corresponding spectra. Columns display the maps for a single scan. Note that the final column in Figures 4 and 5 display maps for the same participant, scanned twice. See reference [2] for corresponding maps calculated with a voxelwise spectral approach.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4421