Introduction

Water exchange is mostly ignored in the models of quantitative diffusion, such as White Matter Tract Integrity (WMTI) ¹. However, recent studies have suggested that the water exchange still significantly affects MRI measures of tissues ex vivo ² and in vivo ³. Here, we performed Monte Carlo (MC) simulations to investigate how water exchange process contributes to the WMTI-based metrics, namely axon water fraction (AWF) and mean kurtosis (MK).

Theory

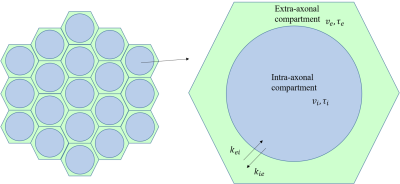
Based on biophysical reality, there are three compartments, namely intra-axonal (i), myelin sheath (m), and extra-axonal (e) compartments in the neuronal microenvironment. When water exchange among different compartments is considered, they can be modeled by a probabilistic change in the state of a molecule $$$s(t)$$$, which is described by a probability vector $$$\boldsymbol{p}(t)=[p_{i}(t), p_{m}(t),p_{e}(t)]'$$$ with $$$p_{i,m,e}(t)$$$ being the probability of each compartment. Owing to exchange, the probability distribution evolves as follows,$$\frac{\mathrm{d} \boldsymbol{p}(t)}{\mathrm{d} t}=K\boldsymbol{p}(t), (1)$$where the matrix $$$K$$$ is given by$$K: = \begin{bmatrix}-k_{im} &k_{mi} &0 \\ k_{im} &-k_{mi}-k_{me} &k_{em} \\ 0 &k_{me} &-k_{em} \end{bmatrix}, (2)$$ and $$$k_{im}$$$ and $$$k_{mi}$$$ are water exchange rates between intra-axonal compartment and myelin while $$$k_{em}$$$ and $$$k_{em}$$$ are water exchange rates between extra-axonal compartment and myelin. Given that signals from myelin could not be detected as assumed in WMTI model ¹, we simplified Eq. (2) to $$K: = \begin{bmatrix}-k_{ie} &k_{ei}\\ k_{ie} &-k_{ei}\end{bmatrix}, (3)$$ Then signal is given by$$\begin{bmatrix}\frac{\partial s_{i}}{\partial t}\\ \frac{\partial s_{e}}{\partial t}\end{bmatrix}=\begin{bmatrix}-q^{2}D_i-k_{ie} &k_{ei} \\ k_{ie} &-q^2D_i-k_{ei} \end{bmatrix}\begin{bmatrix}S_i(q,t)\\ S_e(q,t)\end{bmatrix}. (4)$$
For the kurtosis and AWF, we obtain,$${MP}_p(\cdot )={MK}_a(\cdot )\cdot h(\cdot ), (5)$$ $$AWF=\frac{K_{max_a}\cdot h(\cdot )}{K_{max_a}\cdot h(\cdot )+3}, (6)$$
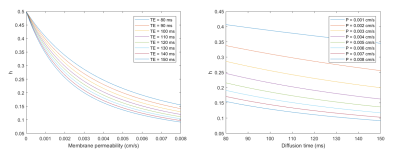
where $$$MK_p(\cdot )$$$ is mean kurtosis value in presence of water exchange while $$$MK_a(\cdot )$$$ is mean kurtosis value in absence of water exchange, and $$$h(\cdot )$$$ is derived previously,⁴$$h(\cdot )=\frac{1}{k_{ie}\cdot \frac{1}{v_i}\cdot \Delta }-\frac{1}{{(k_{ie}\cdot \frac{1}{v_i}\cdot \Delta )}^{2}}+\frac{e^{-k_{ie}\cdot \frac{1}{v_i}\cdot \Delta }}{{(k_{ie}\cdot \frac{1}{v_i}\cdot \Delta )}^{2}}, (7)$$
where $$$k_{ie}$$$ is water exchange rate from intra- to extra-axonal compartment, and $$$k_{ie}=P\cdot \frac{area}{volume}$$$, $$$v_i$$$ is the volume fraction of intra-axonal compartment, in other words, model-defined AWF.

Methods

MC simulations of random walkers and signal analysis were implemented in MATLAB (Version 2017b, MathWorks, Natick, MA, USA). Model is built as shown in Fig. 1. Intrinsic diffusivities ($$$D_{0,e}$$$ , $$$D_{0,i}$$$) were 2 and 1 $$$\mu m^2/ms$$$. Water exchange between intra- and extra-axonal compartment is given as $$$P_{ie}=4P/\sqrt{6D_i/dt}$$$ and $$$P_{ei}=4P_{ie}/\sqrt{D_i/D_e}$$$, where $$$P$$$ is membrane permeability. $$$P$$$ varied from 0.001 to 0.008 $$$cm/s$$$, with a step length of 0.001 $$$cm/s$$$. Other settings are described by Lin M et al ⁵.

Results

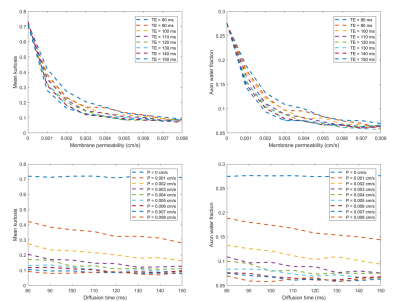
Top row of Fig.2 shows MK and AWF decrease as permeability increases and approach to constants at large membrane permeability, based on MC. Bottom row shows MK and AWF changes with diffusion time. When permeability is 0, MK and AWF do not vary with diffusion time, however, they vary when permeability is larger than 0 and approach to constants at large diffusion time. The simulation results are consistent with analytical solutions shown in Fig.3.
Fig. 3 shows changes of $$$h(\cdot )$$$ with membrane permeability and diffusion time, from analysis of (7) and related equations.

Discussion and Conclusion

Simulation results and analytical solutions show that membrane permeability has non-negligible effect on the dMRI metrics. And when membrane permeability is taken into account, diffusion time will also affect them. Furthermore, it should be noted that $$$h(\cdot)$$$ contains term of axonal volume fraction, which is the model-defined AWF, thus AWF derived from Eq. (6) is not a metric corresponding to axonal content as previously assumed ¹. In this study, we highlight the effects of membrane permeability on WMTI-derived dMRI metrics, which should not be neglected.

Acknowledgements

This work was supported by the National Natural Science Foundation of China [grant numbers 91632109, 81871428, 81971184], the Shanghai Key Laboratory of Psychotic Disorders [grant number 13dz2260500], the Major Scientific Project of Zhejiang Lab [grant number 2018DG0ZX01], and the Fundamental Research Funds for the Central Universities [grant number 2019QNA5026].