Introduction

Diffusion MRI data is typically fit to signal models using linear least squares (LLS). Since the log-transform from linearization leads to heteroscedastic amplification of Rician noise, weighted linear least squares (WLLS) is generally preferred over ordinary linear least squares (OLLS).^1-3 While WLLS places higher weights on data with higher SNR, low SNR data are often integral for model fitting, particularly in the case of high b-value data, which are relied upon for fitting higher-order signal models such as diffusion kurtosis imaging (DKI).

In this work we compare the performance of OLLS and WLLS in single-shell DTI, multi-shell DTI and multi-shell DKI. We demonstrate that strictly assigning lower weights to shells of higher b-values may be a suboptimal approach. To counteract this potential pitfall, we propose a novel “nested” WLLS weighting scheme for multi-shell models in which each shell is assigned a relative weight, with standard WLLS applied within each shell.

Methods

Simulations
For DTI, ground-truth parameters were simulated as [D_xx,D_xy,D_xz,D_yy,D_yz,D_zz]=[1.6,0.2,0.2,0.5,0.2,0.3] (units μm²/ms) and S₀=1. The DTI model was then synthesized with 30 directions b=1000s/mm², 3 b=0 for the single-shell case, and 30 directions b=700s/mm², 30 directions b=1000s/mm², 30 directions b=1300s/mm², 3 b=0 for the multi-shell case.
For DKI, ground-truth parameters were simulated as [D_xx,D_yy,D_zz,W_yyyy,W_zzzz,W_yyzz]=[1.6,0.5,0.3,0.3,0.1] and the 15 other parameters as zero. The DKI model was then synthesized with 30 directions b=1000s/mm², 30 directions b=2000s/mm², 6 b=0.
In all cases, Rician noise was added to the synthesized signal with SNR=20, defined by SNR=S0/σ(η) where η is randomly taken from a normal distribution.

LLS Procedure
S₀ was computed as the average of data with b=0 (as opposed to being fit as a free parameter). All other parameters were represented by vector x, which has 6 dimensions for DTI and 21 dimensions for DKI. Defining a as the normalized signal for all b>0 images, x is computed by

x = (H^T W H)^-1 H^T W ln(a)

where H is the design matrix (respective for DTI or DKI) and W = diag(w_i) is the weight matrix. For OLLS, w_i = 1. For standard WLLS, w_i = s_i², where s=exp(H x_OLLS) to avoid noise biasing the weights.³ For DKI, a novel “nested” WLLS approach assigns a relative weight to each shell , i.e.

w_i = w_shell * s_i² / Σ_shell s_i².

For standard WLLS, w_shell = Σ_shell s_i². For the nested WLLS approach explored in this study, w_shell = 1 (i.e. equal weights) for all shells.

For each of single-shell DTI, multi-shell DTI and multi-shell DKI, the fit was performed for 10,000 iterations with independent noise realizations. The mean and standard deviation of the fitted parameters was computed for each of the three experiments. Relative error in each parameter was calculated as |fitted - ground-truth value| / |ground-truth value|.

Results

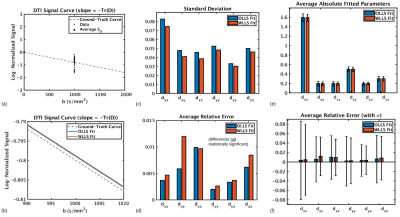
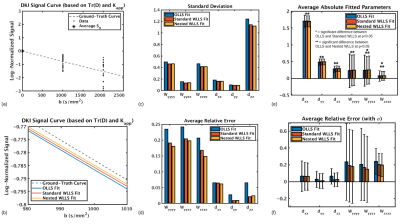
For simulations based on conventional single-shell DTI (Figure 1), WLLS improves the precision of fitted parameters over OLLS, although WLLS does not improve the accuracy, which is already very high with OLLS (if SNR is lowered to 10, the accuracy of OLLS is reduced and WLLS improves the accuracy; simulation not shown). If multiple shells are used to fit DTI (Figure 2), the OLLS fit has lower accuracy than for single-shell (compare Figure 1d and Figure 2d) with the introduction of unnecessary noisy data. If DTI is fit with WLLS, adding more shells improves accuracy. Furthermore, adding shells to the DTI fit improves precision for both the OLLS and WLLS fit (compare Figure 1c and 2c), and WLLS improves the precision over OLLS. Table 1 illustrates how WLLS weighs higher b-shells lower.

For fitting DKI (Figure 3), both standard WLLS and nested WLLS (with equal weighting for each shell) improve the precision of fitted parameters, but only nested WLLS significantly improves the accuracy of all fitted parameters. Table 2 illustrates how standard WLLS weighs higher b-shells lower while nested WLLS weighs shells equally.

Discussion

This study demonstrates (1) a DTI fit does not require multiple shells, so adding shells does not improve fitting accuracy for OLLS, but WLLS does improve multi-shell DTI accuracy by lowering the contribution of unnecessary higher shells; and (2) for a DKI fit which does depend on multiple shells, a nested WLLS may be beneficial over standard WLLS. As such, this study illustrates how strictly assigning shells with higher b-values with lower weights may not be optimal for fitting models dependent on multiple shells.

For the proposed nested WLLS in this work, each shell was assigned an equal weight, but nested WLLS can allow for any possible relative weights between shells, for example, weights can be assigned proportional to the number of directions in a shell. In nested WLLS, standard WLLS is applied within each shell because this is well-known to improve precision in fitting single-shell models (e.g. Figure 1c).

Conclusion

Standard WLLS weighs higher b-shells lower. This fact is beneficial when fitting multi-shell data to models not dependent on multiple shells (e.g. DTI), but may not be beneficial when fitting models that do depend on multiple shells (e.g. DKI). While standard WLLS still increased the accuracy and precision of the fit of multi-shell models over OLLS in this study, the proposed nested WLLS outperformed standard WLLS.

Acknowledgements

We thank National Sciences and Engineering Research Council (NSERC) of Canada and the National Institutes of Health (NIH) for financial support.