Introduction

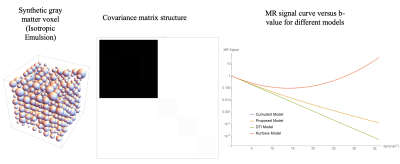
Estimating a diffusion tensor distribution (DTD) within a voxel has the potential to reveal features of the underlying microstructure in unprecedented detail. However, a proper model relating the MR signal to microstructure is critical for achieving such super-resolution. Jian et al. proposed a signal model [1] for an arbitrary DTD, p(D), in the Gaussian diffusion regime assuming a discrete mixture of Wishart distributions for p(D). The diffusion tensor imaging (DTI) model [2] effectively assumes p(D) to be a delta function. The kurtosis [3] and cumulant models [4] while not assuming a parametric form for p(D) are limited to be used at low b-values due to the unphysical global minimum they possess in their signal curves (Figure 1). This effectively limits the amount of microstructure information that one could glean from such models given that DTI successfully accounts for most of the signal at low b-values. Here a new signal model is proposed which is monotonically decreasing for all b-values, overcoming the limitations of the kurtosis and cumulant models. A theoretical framework is also developed for validating the estimated DTD from the new model using synthetic data, providing a proof of principle.

Methods

A multi-normal distribution constrained within the manifold of positive semi-definite diffusion tensors,$$$\mathcal{M}^+$$$, is proposed for p(D) that is fully characterized by the mean and covariance tensors. It is based on the application of the central limit theorem, which is justified by the large voxel size of typical MRI scans and the large number of micro voxels they contain. The resulting signal model is given by,
$$S(\mathbf{b}) = S_0 e^{-\mathbf{b}.\overline{\mathbf{D}}+\frac{1}{2}\mathbf{b}.\Sigma\mathbf{b}} \frac{Z[\overline{\mathbf{D}}-\Sigma.\mathbf{b},\Sigma]}{Z[\overline{\mathbf{D}},\Sigma]}$$
where b is a 2nd-order b-tensor and $$$\overline{\mathbf{D}}$$$ is a 2nd-order mean diffusion tensor transformed into 6 x 1 vectors, ∑ is the 4th-order covariance tensor transformed into a 6 x 6 matrix [5], and $$$Z$$$ is the partition function given by,
$$Z[\overline{\mathbf{D}},\Sigma] = \int_{\mathcal{M}^+} e^{-\frac{1}{2}(\mathbf{D}-\overline{\mathbf{D}})\Sigma^{-1}(\mathbf{D}-\overline{\mathbf{D}})} d\mathbf{D}$$
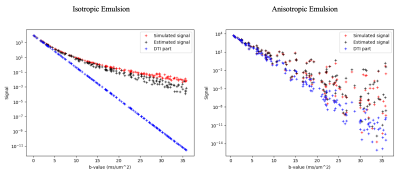
It can be shown that the above constrained multi-normal distribution has the maximum entropy among all probability distributions supported in $$$\mathcal{M}^+$$$ which makes the proposed signal model unique for a given constrained mean and covariance tensors. The ability to estimate the mean and covariance tensors from the MR data is shown using the following simulation framework. Synthetic MR signals were generated using the above model for DTDs with known mean and covariance. Monte Carlo integration was used to evaluate the integrals in the signal expression. Gaussian noise was added to the signal in quadrature such that the signal-to-noise ratio was 10 for the largest b-value simulated. The noisy signals were then used to estimate the mean and covariance by fitting the data to the model using nonlinear least-squares routine. Given the uniqueness of the signal model, the efficacy of the estimation was evaluated by comparing the simulated signal with that computed based on the estimated parameters.

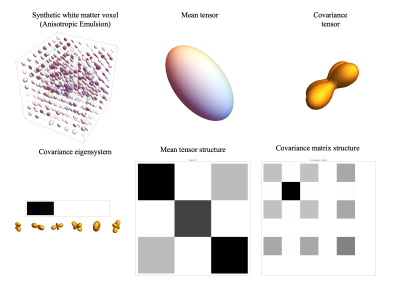
Two different DTDs were simulated--one each for gray and white matter. The gray matter voxel was synthesized by generating microvoxel samples from a multi-normal distribution with an isotropic mean and a covariance tensor characterized by two constants, λ and μ [4], [5] resulting in an emulsion of micro diffusion tensors for λ ≠ 0 and μ = 0 (Figure 1). White matter voxels were generated by fixing the eigenvectors of the micro diffusion tensors along the principal fiber directions while randomly picking eigenvalues from a constrained normal distribution such that they are always positive with mean $$$D_\parallel = 2 D_\perp$$$ and $$$\sigma_{D_\parallel} << \sigma_{D_\perp}$$$ (Figure 2). Such a tensor distribution is expected to be observed in aligned white matter fiber bundles in a voxel consisting of axons with different major and minor radii [6].

Results and Discussion

The simulated white matter voxel is shown in Figure 2 along with the structure of its mean and covariance tensors. The mean tensor is anisotropic along the principal fiber directions as expected while the covariance tensor glyph shows the axis of maximum variance in the transverse plane as expected shown by the cross-like structure perpendicular to the fiber axes. The resulting full 6 x 6 covariance matrix is also markedly richer compared to the isotropic emulsion case shown in Figure 1, estimated in other imaging studies using the cumulant model [4]. The results of the model fit are shown in Figure 3 for both the voxels showing good agreement between the simulated and estimated data. This work demonstrates the ability of this framework to estimate both the 2-parameter isotropic and 21-parameter general covariance matrices from MR data. In practice, large b-value acquisitions are required to reliably estimate the covariance structure, which are increasingly available clinically with the advent of “connectome-type” MRI scanners.

Conclusion

A new model for estimating a normal DTD is proposed which is applicable for any b-value. The covariance tensor, displayed with a 3D glyph, is shown to contain rich intra-voxel microstructural information not previously revealed in other DTD studies. A simulation framework is also presented to establish the feasibility of estimating the mean and covariance of the DTD with realistic SNR values.

Acknowledgements

This work was funded by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, and with some support from the NIH BRAIN Initiative U01- “Connectome 2.0: Developing the next generation human MRI scanner for bridging studies of the micro-, meso- and macro-connectome”, 1U01EB026996-01. We would like to thank Dan Benjamini for insightful discussion.