4405

DeepHIBRID: How to condense the sampling in the k-q joint space for microstructural diffusion metric estimation empowered by deep learning

Qiuyun Fan¹, Qiyuan Tian¹, Chanon Ngamsombat¹, and Susie Y. Huang¹
¹Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States

Synopsis

Conventional diffusion imaging protocols may require tens or hundreds of samples in the q-space to generate reliable maps. Knowing that the k-q joint space is highly redundant and given the tradeoffs between k, q and SNR, we trained a deep convolutional neural network using a HIgh B-value and high Resolution Integrated Diffusion (HIBRID) sampling scheme, dubbed DeepHIBRID. We show DeepHIBRID outperforms conventional sampling schemes, and is capable of outputting 14 synthesized diffusion metric maps simultaneously with only 10 input images, without sacrificing the quality of the output maps, using 30x angular downsampling.

Introduction

Conventional imaging protocols that are capable of generating reliable maps of DTI, NODDI or other diffusion models usually require tens or hundreds of samples in q-space, which renders the acquisition too time-consuming to be clinically feasible. While both k-space1 and q-space2,3 are highly redundant, physically/analytically modeling the k-q space4,5 to make use of this redundancy is challenging. However, recent work employing deep learning techniques to achieve either super resolution in the “k”-dimension6-9 or heavily down-sampling in the “q”-dimension2,10 reveals great potential of the tool in condensing the acquisition sampling schemes. In practice, image SNR decreases as either k or q increases, yielding the sought after HIgh B-value and high Resolution Integrated Diffusion (HIBRID) acquisition11. Enlighted by previous work mentioned above, we investigated the feasibility of condensing the k-q space jointly using a deep Convolutional Neural Network (CNN).

Methods

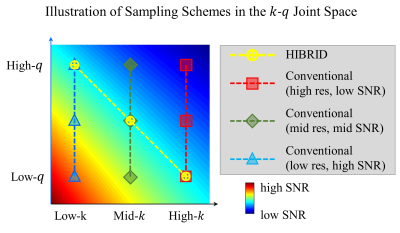
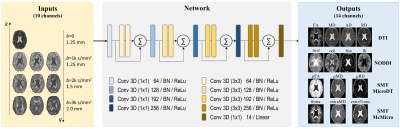
HCP Data Pre-processed diffusion MRI data of 90 subjects (56 for training, 14 for validation, 20 for testing) from the Human Connectome Project (HCP) WU-Minn-Oxford Consortium were used12. Diffusion data were acquired at 1.25-mm isotropic resolution (i.e., native resolution) at b=1000, 2000 and 3000 s/mm2 shells, each with 90 uniform diffusion-encoding directions, along with 18 interspersed b=0 volumes.
Pipeline The inputs to the network are: a single b=0 image, 3 DWIs from each shell (total 10 input channels). The first 3 diffusion-encoding directions in each shell were selected, which are largely uniformly distributed on the sphere and consistent across all subjects. Inputs of 4 sampling schemes of various spatial resolutions (and hence SNR levels) are compared (Figure 1), where spatial downsampling was achieved by Fourier transforming the imaging into k-space, which was lowpass-filtered and inverse Fourier transformed back to image space.
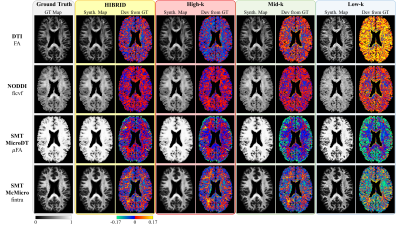
The outputs of the network are: microstructural parameter maps of 4 diffusion models: DTI (FA, MD, RD, AD), NODDI13 (ficvf, fiso, odi, fh=1-ficvf-fiso), SMT-MicroDT14 (FA, MD, RD), SMT-McMicro15 (fintra, extraMD, extraTrans), yielding a total of 14 output channels at 1.25-mm isotropic resolution. The Ground Truth (GT) maps were calculated by feeding the original dataset (270 DWIs + 18 b0s at 1.25-mm) to the 4 above mentioned diffusion models.
A deep 3-dimensional plain CNN16-18 with ResNet structure, adapted on top of Gibbons et. al10, was used to learn the mapping from the input to the GT quantitative maps (Figure 2). The network along with HIBRID inputs is referred to as DeepHIBRID in this work.

Results

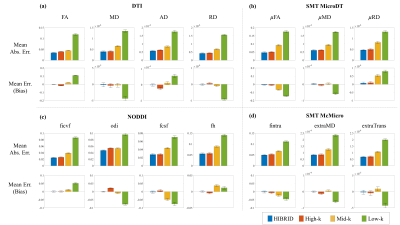
The output maps of diffusion metrics were similar to the GT maps, with the highest accuracy achieved by the HIBRID sampling scheme (Figure 3) and decreasing accuracy as higher spatial downsampling ratio was used for conventional sampling schemes. The residuals between the output and GT maps did not contain obvious anatomical structure for the HIBRID and High-k sampling schemes, but some degree of anatomical structure are appreciable for the Mid-k and Low-k schemes.
A summary of the performance in synthesizing the diffusion metrics is shown in Figure 4, where the HIBRID sampling scheme consistently outperforms the conventional schemes in all diffusion models/metrics with both higher accuracy and lower bias. Among the conventional sampling schemes, the High-k scheme gives the best overall performance, although the other two schemes yield higher accuracy and/or less bias depending on diffusion models and metrics.

Discussion

The DeepHIBRID network performs simultaneous denoising and super-resolution by leveraging the data redundancy in the k-q joint space, achieving a 30 fold angular resolution downsampling without sacrificing the quality of estimated maps, which is barely feasible via conventional parametric approaches. The deep CNN approach generates 14 channels of output maps with only 10 channels of input images, which is indicative of the great degree of redundancy not only in the k-q joint space on the input side, but also in the parameter maps on the output side.
In comparing the different sampling schemes, HIBRID outperforms all conventional sampling schemes, demonstrating the advantage of the HIBRID acquisition scheme using a highly complicated nonlinear data-driven approach. Among the conventional sampling schemes, accuracy decreases and bias increases as more spatial smoothing is introduced, even though the SNR presumably increases. On the output maps synthesized with Low-k sampling scheme, artificial high-frequency structures can be appreciated by visual inspection. These results put together indicate that super resolution might be a more demanding task that may need a more dedicated network to render better performance, whereas denoising appears to be a less challenging task for 3D CNNs.

Conclusions

The DeepHIBRID network demonstrates the capability of outputting 14 maps of diffusion metrics simultaneously with only 10 input images, achieving both denoising and super resolution with 30 fold angular downsampling without sacrificing the quality of the estimated maps, a task that is barely feasible via conventional model-fitting approaches.

Acknowledgements

This work was supported by NIH U01EB026996

References

1 Haldar, J. P., Fan, Q. & Setsompop, K. in Proc. ISMRM. 0102.

2 Golkov, V. et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Transactions on Medical Imaging 35, 1344-1351, doi:10.1109/TMI.2016.2551324 (2016).

3 Schwab, E., Vidal, R. & Charon, N. 475-483 (Springer International Publishing).

4 Sotiropoulos, S. N. et al. Fusion in diffusion MRI for improved fibre orientation estimation: An application to the 3T and 7T data of the Human Connectome Project. Neuroimage 134, 396-409, doi:10.1016/j.neuroimage.2016.04.014 (2016).

5 Sotiropoulos, S. N. et al. RubiX: combining spatial resolutions for Bayesian inference of crossing fibers in diffusion MRI. IEEE Trans Med Imaging 32, 969-982, doi:10.1109/TMI.2012.2231873 (2013).

6 Alexander, D. C. et al. in Proc. ISMRM. 0563.

7 Ledig, C. et al. in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 105-114.

8 Kim, J., Lee, J. K. & Lee, K. M. in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 1646-1654.

9 Dong, C., Loy, C. C., He, K. & Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295-307, doi:10.1109/tpami.2015.2439281 (2016).

10 Gibbons, E. K. et al. Simultaneous NODDI and GFA parameter map generation from subsampled q-space imaging using deep learning. Magnetic Resonance in Medicine 81, 2399-2411, doi:10.1002/mrm.27568 (2019).

11 Fan, Q. et al. in Proc. ISMRM. 1041.

12 Glasser, M. F. et al. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105-124 (2013).

13 Zhang, H., Schneider, T., Wheeler-Kingshott, C. A. & Alexander, D. C. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61, 1000-1016, doi:10.1016/j.neuroimage.2012.03.072 (2012).

14 Kaden, E., Kruggel, F. & Alexander, D. C. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn Reson Med 75, 1752-1763, doi:10.1002/mrm.25734 (2016).

15 Kaden, E., Kelm, N. D., Carson, R. P., Does, M. D. & Alexander, D. C. Multi-compartment microscopic diffusion imaging. Neuroimage 139, 346-359, doi:10.1016/j.neuroimage.2016.06.002 (2016).

16 Zhang, K., Zuo, W., Chen, Y., Meng, D. & Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing 26, 3142-3155 (2017).

17 Kim, J., Kwon Lee, J. & Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1646-1654 (2016).

18 Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. Preprint at: https://arxiv.org/abs/1409.1556 (2014).

Figures

Figure 1. Illustration of sampling schemes in the k-q joint space. Image SNR depends on spatial resolution (k) and diffusion weighting (q). Conventionally, multi-shell diffusion data were acquired with fixed k, as illustrated by the Low-k (marked in triangles), Mid-k (diamonds), and High-k (squares) protocols, with their corresponding pros and cons in resolution and SNR. Hereby, the HIBRID imaging sampling scheme is motivated by the SNR trade-offs, and advises to acquire lower shells with higher spatial resolution, and higher shells with lower resolution.

Figure 2. Layout of the network and its inputs and outputs. A 3D Convolutional Neural Network is used, with increased number of filters in deeper layers. The input layer takes 10 channels which is comprised of 1 b0, 3 b1k, 3 b2k and 3 b3k diffusion weighted images. The output layer gives 14 synthesized maps of microstructural diffusion metrics, mimicking the outputs from the DTI, NODDI, Spherical Mean Technique (SMT) micro-Diffusion Tensor (microDT), and SMT Multi-compartment Microstructural imaging (SMT McMico) methods.

Figure 3. Synthesized maps using 9 DWIs compared with the Ground Truth (GT) maps calculated with 270 DWIs demonstrated in one representative subject. One exemplary map from each of the models are shown, with their deviation from the GT maps presented side by side. HIBRID gives the best accuracy among all the sampling schemes. The accuracy decreases as spatial resolution decreases. It appears that the network starts to synthesize extra fine structures on the map using the Low-k scheme, whereas the low SNR in the High-k dataset seems to be a relatively easier task for the network to handle.

Figure 4. Comparison of network performance among sampling schemes. The mean Absolute Error (Abs Err, reflecting accuracy) and mean Err (reflecting bias) were calculated across all brain tissue voxels. CSF was excluded from training and thus testing assessment as well. The HIBRID consistently outperforms other sampling schemes in all diffusion models/metrics with higher accuracies and lower biases. Among the conventional sampling schemes, the High-k scheme gives the best overall performance, although the other two can achieve higher accuracy or lower bias occasionally.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4405