4401
Lesion detection using Free-Water elimination DTI - is this technique really specific to free water?1ISR-Lisboa/LARSyS and Department of Bioengineering, Instituto Superior Técnico – Universidade de Lisboa, Lisbon, Portugal, Lisbon, Portugal, 2Champalimaud Neuroscience Programme, Champalimaud Centre for the Unknown, Lisbon, Portugal, Lisbon, Portugal
Synopsis
Free water elimination (FWE) for diffusion tensor imaging (DTI) aims to decouple the free water contribution from tissue's diffusion. Recent studies suggest that FWE-DTI is essential to characterize degenerative processes since it suppresses free water partial volume effects from DTI analysis and provides an index sensitive to edema and tissue degeneration. In this work, the state-of-the-art of FWE-DTI estimation is explored and several fitting procedures are tested on in vivo data to which simulated lesions were added. We found that, unlike the multi-shell approach, the single-shell implementation was unable to discriminate between changes in tissue diffusion and free water increases.
Introduction
When multiple tissue compartments are present in a voxel, their contributions are averaged and interpreting diffusion scalar metrics becomes difficult.1 In particular, free water (FW) contamination inflates the tissue’s diffusion tensor at cerebrospinal fluid interfaces or due to edema. To mitigate this issue, a FW elimination model was proposed (FWE-DTI), extending the DTI model by also considering the contribution of a FW component to the dw-MRI signal.2 Recent studies suggest that this technique can characterize tissue diffusion in neurodegenerative diseases3-6: FWE-DTI suppresses FW contamination and provides an estimate of the FW fraction, which could be used as a surrogate marker for edema and tissue degeneration.7 Moreover, FWE-DTI has also attracted great interest due to its potential compatibility with clinically acquired data.Fitting procedures for FWE-DTI have been proposed for data acquired with both single7 or multiple b-values8, however, no study had previously been performed to objectively compare their accuracy. In this study, the state-of-the-art FWE-DTI fitting procedures are explored and their performance is tested on in vivo data to which simulated lesions were added.
Methods
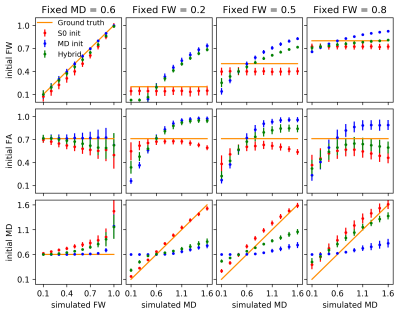
1) InitializationFitting the FWE-DTI model to single-shell data presents an ill-posed problem9, the initial guess for FW is crucial to stabilize the fit. Three initialization methods were implemented: 1) based on the unweighted image S0 ; 2) based on the initial Mean Diffusivity (MD) and assuming a constant $$$MD_t=0.6\times10^{-3}mm^2s^{-1}$$$ for healthy tissue ; 3) a log-linear interpolation between methods 1 and 2.10
2) Regularized gradient descent (GD)
To further stabilize the fit, a regularization operator is used to enforce spatial smoothness to the tensor field while the parameters are updated with GD.7,11 This algorithm was implemented within the open-source package Diffusion Imaging in Python (Dipy)12 and was generalized to be compatible with both single and multi-shell acquisitions.
3) Conventional nonlinear least squares (NLS) - multi-shell only
A multi-shell procedure was previously implemented in Dipy.13 This approach does not depend on spatial constraints for convergence, instead it uses a modified NLS search to fit to the data.8
4) MRI data
Data available in Dipy was used in this study; it was acquired on a Siemens Trio 3T, with b-values from $$$200-3000 \ s \ mm^{-2}$$$ in steps of $$$200 \ s \ mm^{-2}$$$ (32 directions per shell), a single S0 was acquired. Only volumes acquired with $$$b\leq1000 \ s \ mm^{-2}$$$ were included to avoid tissue’s non-Gaussian diffusion effects.14
5) Simulations and processing
A tensor was simulated with varying levels of FW contamination for a single voxel and 100 noise instances. The initialization method with the smallest mean error was used for subsequent FWE-DTI runs.
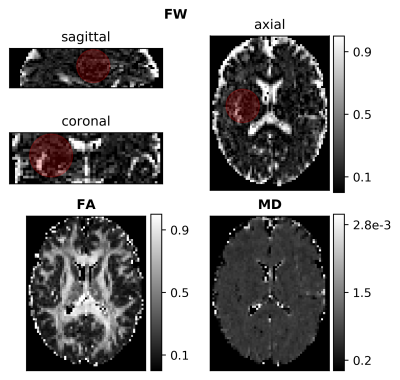
The NLS FWE-DTI routine was applied to the in vivo DW volumes to obtain ground truth (GT) tissue DT and FW maps. Lesions with radius of $$$16 \ mm$$$ were simulated by altering the GT FW or DT separately. Two types of lesions were simulated: 1) FW fraction set to 0.6; 2) simulating a tissue structure alteration that increases the MD while preserving the Fractional Anisotropy (FA) - for this the eigenvalues of the DT were multiplied by $$$(1.5\times10^{⁻3})/MD_{GT}$$$.
After generation of the synthetic lesions, single-shell ($$$b=1000 \ s \ mm^{-2}$$$, 32 directions) and multi-shell ($$$b=500$$$, $$$1000 \ s \ mm-^{2}$$$, 32 directions each) datasets were simulated by applying the forward model to the GT FW map and DT field. In total, 4 synthetic datasets were produced (2 lesion types$$$\times$$$2 acquisition protocols), and corrupted with rician noise ($$$SNR=40$$$). Data were processed with standard DTI, regularized GD FWE-DTI (200 iterations; learning rate of 0.0006) and NLS FWE-DTI. The estimated diffusion metrics (FW and MD) were compared with the GT.
Results
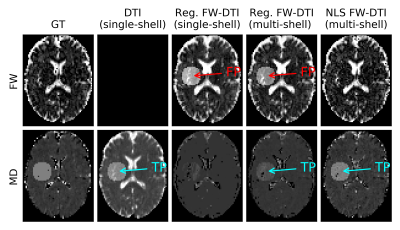
The hybrid initialization performed better than the other two initialization methods in the single-voxel simulations (Fig.1), although the performance decreased when the GT MD deviated from the assumed MDt.The GT parameters extracted from the MRI data are presented in Fig.2, on which the location of the simulated lesions is displayed. The FW lesion (Fig.3) was detected as a region with increased MD by DTI, while all FWE-DTI methods identified changes in FW. However, the regularized GD (single-shell) estimated a flat MD map due to the constant MDt assumption during initialization.
The MD lesion (Fig.4) was correctly resolved by DTI, but the regularized fitting approach erroneously estimated an increased FW (for both single- and multi-shell cases); NLS FWE-DTI was able to identify the correct type of change for both lesions.
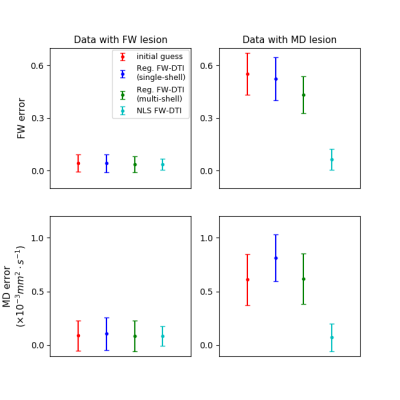
The visual assessment is supported by the absolute error per voxel inside the lesion mask (Fig.5), NLS FWE-DTI has the smallest mean bias and dispersion for the estimated FW and MD in both types of lesions.
Conclusion
Although the regularized GD FWE-DTI is sensitive to FW alterations in the dw-MRI signal, it may lack the specificity to discriminate these lesions from tissue alterations that lead to increased MD. In future studies, metrics estimated with single-shell FWE-DTI should hence be interpreted with care.Acknowledgements
Portuguese Foundation for Science and Technology (FCT - IF/00364/2013, UID/EEA/50009/2019).References
1. Alexander, A. L., et al. (2001). Analysis of partial volume effects in diffusion‐tensor MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 45(5), 770-780.
2. Pierpaoli, C., & Jones, D. K. (2004). Removing CSF contamination in brain DT-MRIs by using a two-compartment tensor model. In International Society for Magnetic Resonance in Medicine Meeting (p. 1215).
3. Ofori, E., et al. (2015). Increased free water in the substantia nigra of Parkinson's disease: a single-site and multi-site study. Neurobiology of aging, 36(2), 1097-1104.
4. Ofori, E., et al. (2015). Increased free water in the substantia nigra of Parkinson's disease: a single-site and multi-site study. Neurobiology of aging, 36(2), 1097-1104.
5. Planetta, P. J., et al. (2015). Free-water imaging in Parkinson’s disease and atypical parkinsonism. Brain, 139(2), 495-508.
6. Ofori, E., et al. (2017). Free water improves detection of changes in the substantia nigra in parkinsonism: A multisite study. Movement Disorders, 32(10), 1457-1464.
7. Pasternak, O., et al. (2009). Free water elimination and mapping from diffusion MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 62(3), 717-730.
8. Hoy, A. R., et al. (2014). Optimization of a free water elimination two-compartment model for diffusion tensor imaging. Neuroimage, 103, 323-333.
9. Scherrer, B., & Warfield, S. K. (2010, April). Why multiple b-values are required for multi-tensor models. Evaluation with a constrained log-Euclidean model. In 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (pp. 1389-1392). IEEE.
10. Ismail, A. A. O., et al. (2018, September). Characterizing peritumoral tissue using DTI-Based free water elimination. In International MICCAI Brainlesion Workshop (pp. 123-131). Springer, Cham.
11. Gur, Y., et al. (2009). Fast GL (n)-invariant framework for tensors regularization. International journal of computer vision, 85(3), 211.
12. Garyfallidis, E., et al. (2014). Dipy, a library for the analysis of diffusion MRI data. Frontiers in neuroinformatics, 8, 8.
13. Henriques, R. N., et al. (2017). [Re] Optimization of a free water elimination two-compartment model for diffusion tensor imaging. BioRxiv, 108795.
14. Hansen, B., & Jespersen, S. N. (2016). Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Scientific data, 3, 160072.
Figures