Introduction

There is a clinical need for fast, high contrast, diffusion magnetic resonance imaging (dMRI) techniques that are sensitive to changes in tissue structure and provide diagnostic signatures at the early stages of disease. Here we describe a new way to minimise the acquisition of multi-shell b-value diffusion data, Quasi-Diffusion MRI (QDI). QDI is based on a special case of the Continuous Time Random Walk (CTRW) model of diffusion dynamics^1,2 and assumes presence of non-Gaussian diffusion properties within tissue microstructure. We present a framework for multi-directional diffusion gradient acquisition and data processing that allows computation of Quasi-Diffusion-Weighted Imaging (QDWI) and Quasi-Diffusion Tensor Imaging (QDTI) maps. We show that QDI provides excellent tissue contrast using standard clinical MRI gradients in short acquisition times. Finally, we apply QDI to 3 patient cases.

Methods

Theory
We propose a simplification of the CTRW model^1,2 by a coupling of the $$$\alpha$$$ (waiting time) and $$$\beta$$$ (step length) exponents. Mean squared displacement of diffusing particles in the CTRW model is given by $$$<x^2>\sim t^{2\alpha/\beta}$$$ and Gaussian diffusion by $$$\alpha=1$$$ and $$$\beta=2$$$, such that $$$<x^2>\sim ~t$$$. If the same heuristic Gaussian scaling relation of position with time continues to hold for non-Gaussian diffusion then $$$<x^2>\sim t$$$ and $$$2\alpha/\beta=1$$$. In this case the model represents non-Gaussian diffusion which is not superdiffusive or subdiffusive; instead we have a quasi-diffusion process^2,3. By substitution of $$$2\alpha/\beta=1$$$ in the CTRW dMRI equation⁴ we have,
$$
\begin{align*}
p(q,\bar{\Delta}) &=\sum_{k=0}^{\infty} \frac{(-D_{\alpha,2\alpha}q^{2\alpha}\bar{\Delta}^\alpha)^k}{\Gamma(\alpha k+1)} \\
&=\sum_{k=0}^{\infty} \frac{(-1)^k (D_{1,2} b)^{\alpha k}}{\Gamma(\alpha k+1)}[Eq.1]
\end{align*}
$$
where signal attenuation is parameterised by $$$b=q^2\bar{\Delta}$$$ with $$$\bar{\Delta}=\Delta-\delta/3$$$ (in s) and the diffusion coefficient, $$$D_{1,2}$$$, is in conventional units of mm²s^-1. The fractional a exponent represents a range of properties from Gaussian diffusion ($$$\alpha=1$$$) through non-Gaussian (quasi) diffusion ($$$0<\alpha<1$$$). Specifically, QDI parameterises the signal decay by b-value according to the rate of decay, $$$D_{1,2}$$$, and the shape of the power law tail, $$$\alpha$$$. Crucially $$$\alpha$$$ is analogous to the Diffusional Kurtosis Imaging (DKI) $$$\kappa$$$ measure⁵ as it represents non-Gaussian diffusion dynamics. Estimation of $$$D_{1,2}$$$ and $$$\alpha$$$ along a single diffusion gradient direction requires a minimum acquisition of a b=0 s mm^-2 image and 2 non-zero b-value dMRIs.

QDI acquisition and pre-processing
Our QDI protocol provides voxel resolutions similar to conventional clinical DWI (1.5mm×1.5mm×5mm over 22 axial slices) and utilises ultra-high b-value tissue contrast (TE=90ms, TR=6000ms, b=0, 1100 and 5000 s mm^-2, $$$\delta$$$=23.5ms, $$$\Delta$$$=43.9ms). Data were acquired on a 3T Philips Achieva Dual TX system. QDWI was acquired in 3 orthogonal diffusion gradient directions (acquisition time 84s) and QDTI in 6 and 15 diffusion directions equally spaced on the hemisphere (acquisition times 120s and 228s, respectively). dMRI acquisitions were denoised⁶ and corrected for motion and eddy current distortions⁷.

QDI computation
No image smoothing was performed prior to parameter estimation. $$$D_{1,2}$$$ and $$$\alpha$$$ were estimated in each voxel along each diffusion gradient direction using the Levenberg-Marquadt algorithm and Padé approximation to rapidly estimate Eq.1 and its derivatives⁸. Normalised entropy, $$$H_{n}$$$, was computed along each parameterised decay curve^4,9. QDWI data was averaged in each b-value shell prior to model fitting and computation of mean $$$D_{1,2}$$$, $$$\alpha$$$ and $$$H_{n}$$$ maps. For QDTI, model fitting was performed in each diffusion direction and mean, axial, radial and anisotropy maps were computed from $$$D_{1,2}$$$, $$$\alpha$$$ and $$$H_{n}$$$ tensors¹⁰. Figure 1 shows QDI model fits within representative grey and white matter voxels.

Participants
Six healthy participants were recruited (age 28±8 years). Three patients were also recruited, one with incidental findings of an acute ischaemic infarct (age 75 years), and two brain tumour patients including a WHO Grade II astrocytoma (age 40 years), and a WHO Grade IV glioblastoma (age 58 years).

Results

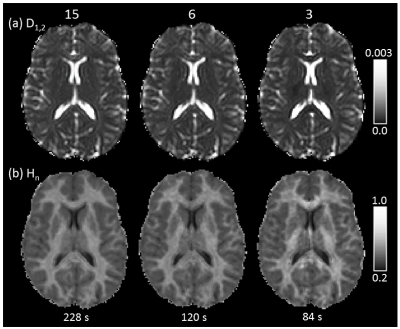
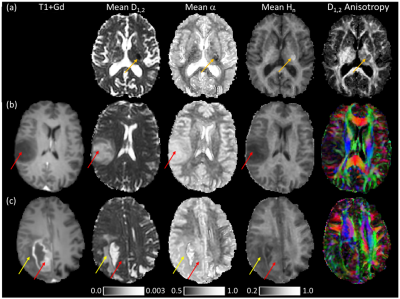
QDI maps and healthy $$$D_{1,2}$$$, $$$\alpha$$$ and $$$H_{n}$$$ values are shown for 15 diffusion gradient direction QDTI in Figure 2 and Table 1. $$$D_{1,2}$$$ maps exhibit similar tissue contrast to conventional dMRI, whereas $$$H_{n}$$$ maps provide tissue contrast analogous to DKI $$$\kappa$$$. Grey and white matter are characterised by non-Gaussian diffusion with greater non-Gaussianity in white matter. Excellent tissue contrast is observed. Figure 3 shows QDI maps computed from short dMRI acquisitions indicating preservation of tissue contrast.

Figure 4a shows an acute infarct with low $$$D_{1,2}$$$ and $$$\alpha$$$, and high $$$H_{n}$$$, corresponding to an increase in restriction of the diffusion environment. The Grade II core (Figure 4b) was characterised by high $$$D_{1,2}$$$ and $$$\alpha$$$, and low $$$H_{n}$$$, and likely represents an infiltrative mix of tumour and normal brain tissue with loss of normal tissue structure. The Grade IV tumour core exhibited low $$$D_{1,2}$$$ and $$$\alpha$$$, and high $$$H_{n}$$$ in regions corresponding to high tumour cellularity where the active angiogenic tumour core is indicated by blood brain barrier breakdown shown by gadolinium contrast enhancement on T1-weighted images (Figure 4c).

Discussion and conclusions

We have shown that QDI generates images with excellent tissue contrast within clinically acceptable acquisition times of between 84 and 228 seconds. QDI provides maps with healthy and pathological tissue contrast similar to DKI^5,11,12 but does so without the limitations of a maximum b-value⁵ allowing exploration of ultra-high b-value dMRI, including anisotropy. Our initial findings suggest that QDI may be added to routine conventional dMRI acquisitions allowing simple translation to the clinical arena.