4398

Anomalous Diffusion estimation through the solution of the Fractional Time order Bloch-Torrey equation

Óscar Peña-Nogales¹, Carlos Castillo^2,3,4, Carlos Lizama⁵, Rodrigo de Luis-Garcia¹, Santiago Aja-Fernández¹, and Pablo Irarrazaval^2,3,4,6
¹Laboratorio de Procesado de Imagen, Universidad de Valladolid, Valladolid, Spain, ²Instituto de Ingeniería Biológica y Médica, Pontificia Universidad Catolica de Chile, Santiago, Chile, ³Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, ⁴Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, ⁵Departamento de Matemáticas y Ciencia de la Computación, Universidad de Santiago de Chile, Santiago, Chile, ⁶Electrical Engineering Department, Pontificia Universidad Católica de Chile, Santiago, Chile

Synopsis

Diffusion-Weighted (DW) imaging has a monoexponential signal decay at low b-values related to the statistical mechanics of Brownian motion. However, at high b-values the DW signal is no longer monoexponential. Various models have been proposed to better fit the data; nevertheless, none of them assumes that the DW signal is governed by the fractional-time order dynamics of the generalized Brownian motion (a.k.a., anomalous diffusion). In this work, by assuming anomalous diffusion we solve the fractional-time order Bloch-Torrey equation for smooth diffusion-weighting gradients and compare the obtained model to existing ones. The proposed model outperforms state-of-the-art on synthetic anomalous phantom experiments.

Purpose

The Diffusion-Weighted (DW) signal is tipically considered to be a monoexponential decay at low b-values where diffusion follows the statistical mechanics of Brownian motion. However, studies^1,2,3 have shown that at high b-values the DW signal deviates from the monoexponential decay. Consequently, there is significant interest in developing models able to phenomenologically explain this deviation. Multiple models have been proposed to understand the actual in-vivo diffusion process, i.e., the empirical stretched exponential⁴ and the kurtosis⁵ models try to explain these deviations through a heterogeneity and non-gaussianity index. More complex models generalize the Brownian motion, where the Mean Square Displacement (MSD) is proportional to the diffusion time, to the Continuous-Time Random Walk (CTRW) where the MSD is represented as the power law $$$\langle{x}^2(t)\rangle~\approx~t^{\alpha/\beta}$$$ where 𝛼 and 𝛽 are the time and space fractional dimensions of the lattice. This generalization converts Gaussian diffusion (𝛼/𝛽=1) into anomalous diffusion (i.e., super-diffusion when 𝛼/𝛽>1 and subdiffusion when 𝛼/𝛽<1)⁶ depending on the complexity, heterogeneity and viscosity of the tissue⁷. Accordingly, the CTRW model⁷ solves the space-time fractional order diffusion equation, and Magin et. al.⁸ introduced the fractional-time/space order Bloch-Torrey equation for the transverse magnetization ($$$M_{xy}({r},t)$$$):

Eq. 1:$$^C_0D^{\alpha}_t\{M_{xy}({r},t)\}~=~-i\gamma(\vec{{r}}\cdot\vec{{G}}(t))M_{xy}({r},t)~+~D\nabla^{2\beta}M_{xy}({r},t),$$

where $$$^C_0D^{\alpha}_t\{\cdot\}$$$ is the Caputo 𝛼th-fractional order time derivative (0<𝛼<=1), $$$\nabla^{2\beta}$$$ the 2𝛽th-fractional order Laplacian operator in space (1/2<𝛽<=1), $$$\vec{{G}}(t)$$$ the time-varying diffusion-weighting gradients, and D the anomalous diffusion coefficient. However, they only solved the Fractional-Space order Bloch-Torrey (FSBT) equation (𝛼=1, 1/2<𝛽<=1) for Stejskal-Tanner gradients, and the Fractional-Time order Bloch-Torrey (FTBT) equation (0<𝛼<=1, 𝛽=1) for the trivial case of a constant gradient. Therefore, no DW-MRI implementable model has been developed for the FTBT which might better explain the nature of the deviations occurring at high b-values. Thus, in this work we solve the Fractional-Time order Bloch-Torrey equation for generalized smooth diffusion-weighting gradients, and validate the proposed model on synthetic anomalous phantom experiments.

Theory

Given the continuous m^th-order smooth polynomial time window functions (w_m) of Singla et. al.⁹, we constructed diffusion-weighting gradient waveforms of spin-echo DWI as $$$\vec{{G}}(\text{t})~=~g\cdot\text{w}_m(\frac{2t-\delta}{\delta})\vec{{r}}~+~g\cdot\text{w}_m(\frac{2(t-\Delta)-\delta}{\delta})\vec{{r}}$$$, where g, 𝛿, and 𝛥 are the gradient strength, duration, and separation, respectively. Then, we solved the FTBT (Eq. 1 for 0<𝛼<=1, and 𝛽=1) for the case of a single gradient in the z-direction ($$$\vec{{r}}~=~\hat{{z}}$$$ and $$$G_z~=~\vec{{G}}(\text{t})\cdot\hat{{z}}$$$). Firstly, the homogeneous solution is $$$M_{xy}(z,t)~=~M_0\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]$$$, where $$$M_{xy}(r,0)~=~M_0$$$, $$$I^{\alpha}_t\{\cdot\}$$$ is the fractional integral of order 𝛼, and $$$\mathrm{E}_\alpha[\cdot]$$$ is the single parameter Mittag-Leffler function¹⁰. Then, by applying truncated versions of the Leibniz rule and the Faá di Bruno’s formula¹¹ for the Caputo operator (note that the m^th-order of the time window functions has to be equal or higher to the index of previous truncations) we obtained the following solution of the Fractional-Time order Bloch-Torrey (FTBT) equation for the transverse magnetization:

Eq. 2:$$M_{xy}(z,t)~=~M_0\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]e^{\int_0^tH(\tau)d\tau},$$

where $$H(t)~=~\frac{-^C_0D^{\alpha}_t\{\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]\}~-~i\gamma{z}G(t)\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]~+~D_\alpha\frac{\partial^2\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]}{\partial{z}^2}}{\alpha^C_0D^{\alpha}_t\{\mathrm{E}_\alpha[-i\gamma{z}\cdot{I}^{\alpha}_t\{G_z(t)\}]\}}.$$

Hereinafter, we numerically evaluate this equation for time window functions of m^th-order m=2.

Methods

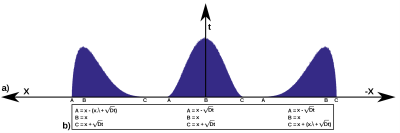
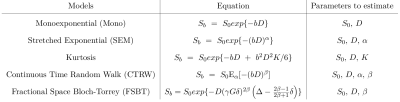
Differently to Brownian motion where the step size of the random walk varies according to a Gaussian distribution, in continuous-time random walks both the waiting time and the jump length can vary according to different fractional distributions. Therefore, we simulated an anomalous diffusion medium through a random walk where the probability density function (PDF) of the jumps depended on the position (x) of each walker, on an asymmetry unitless parameter (𝜆), and on the diffusion parameter D. We used PERT distributions with PDF ($$$f(x)~=~\frac{(x-A)^{a-1}(C-x)^{b-1}}{\text{B}(a,b)(C-A)^{a+b-1}}$$$) (see Figure 1 for details), where $$$a~=~\frac{5B+C-5A}{C-A},~b~=~\frac{5C-A-4B}{C-A}$$$ and B(a,b) is the beta function. To control the time dependence of the MSD of the simulations, the position of each walker was assigned following a stochastic process with a PERT distribution with parameters A, B, and C dependent on x and the diffusion time as shown in Figure 1. Also, note that at x=0 the distribution was always Gaussian.

We simulated various spin-echo DWI acquisitions with 1,000,000 walkers initially at the center of coordinates (x=0) with D=2x10-3mm2/s, 𝜆 in the range of 0-0.5, and diffusion-weighting gradients with 𝛿=5ms, 𝛥=[11,16,21,26]ms, and g=[0,100,200,300,400,500]mT/m, TE = 2𝛥. b-values of each [𝛥,g] pair are shown in Table 1. Estimation of the anomalous diffusion, 𝛼, and/or 𝛽 coefficient was performed with the proposed model (Eq. 2) and models of Table 2 through a non-linear least-squares estimator. Note that some models have the standard values of 𝛼=1 and/or 𝛽=1.

Results

Figure 2 shows the percentage normalized squared error (NSE) of the different models’ estimations, showing a very good fit for the proposed model (FTBT).

Discussion

This preliminary results illustrate the potential of the FTBT model to estimate anomalous diffusion parameters. It achieves lower NSE than any other model. Interestingly, compared to the other models the FTBT takes advantage of DW data from multiple gradient strengths (g) and separations (𝛥), probably due to the non-linear time dependence of the MSD. Nevertheless, detailed in-vivo DWI validation is required to further understand the anomalous diffusion behavior in tissues.

Conclusion

We have developed a new diffusion-weighting signal model solving the Fractional-Time order Block-Torrey (FTBT) equation under the assumption of anomalous diffusion. The proposed model minimizes the NSE compared to state-of-the-art models on synthetic anomalous phantom experiments. This model may have important applications for in-vivo DW-MRI to characterize complex and heterogeneous tissues.

Acknowledgements

The authors acknowledge grant RTI2018-094569-B-I00 from the Ministerio de Ciencia e Innovación of Spain. The main author would also like to acknowledge the Consejería de Educación of Junta de Castilla y León, and the Fondo Social Europeo for his predoctoral grant.

References

1. De Santis S, et al. Non-Gaussian diffusion imaging: a brief practical review. Magn Reson Imaging. 2011;29(10):1410-1416.

2. Clark CA, and Le Bihan D, Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn Reson Med. 2000;44(6):852-859.

3. Jensen JH, et al. Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432-1440. 4. Bennett KM, et al. Characterization of continuously distributed cortical water diffusion rates with a stretched‐exponential model. Magn Reson Med. 2003;50(4):727-734.

5. Steven AJ, et al. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain. Am. J. Roentgenol. 2014;202(1):W26-W33.

6. Metzler R, and Klafter J, The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. 2000;339(1):1-77.

7. Karaman MM, et al. Differentiating low‐and high‐grade pediatric brain tumors using a continuous‐time random‐walk diffusion model at high b‐values. Magn Reson Med. 2016;76(4):1149-1157.

8. Magin RL, et al. Anomalous diffusion expressed through fractional order differential operators in the Bloch–Torrey equation. J Magn Reson. 2008;190(2):255-270.

9. Singla P, et al. Desired order continuous polynomial time window functions for harmonic analysis. IEEE T Instrum Meas. 2009;59(9):2475-2481.

10. Haubold HJ, et al. Mittag-Leffler functions and their applications. J Appl Math, 2011.

11. Lukacs E, Applications of Faà di Bruno's formula in mathematical statistics. Amer. Math. Monthly. 1955;62(5):340-348.

Figures

Figure 1. a) Anomalous diffusion medium simulation over the x-axis . The jump distribution at each position follows a PERT distribution with parameters shown on b). Note that at x=0 the PERT distribution becomes a Gaussian distribution, and that the asymmetry unitless parameter 𝜆 controls the skewness of the distributions away from the origin (x≠0). Larger 𝜆 implies larger sub-diffusive simulated mediums. Further, the $$$\sqrt{Dt}$$$ term controls the diffusion displacement of the random walk. On each simulation all walkers were initially placed at position x=0.

Table 1. Diffusion-weighting b-values [s/mm²] applied in the simulations of the synthetic anomalous phantom experiments for each [𝛥,g] pair. The implemented diffusion-weighting gradient waveforms were based on the m^th-order smooth polynomial time window functions (w_m) of Ref⁹.

Table 2. Signal models for diffusion and anomalous diffusion estimation present in the literature. Particularly, the Monoexponential model assumes Gaussian diffusion, the Stretched exponential and the Kurtosis were initially based on empirical results, and the Continuous Time Random Walk and the Fractional-Space Bloch-Torrey models are based on anomalous diffusion. For simplicity, models are shown here for the Stejskal-Tanner diffusion-weighting gradients. Note that models that do not depend on 𝛼 and/or 𝛽 it is equivalent to consider 𝛼=1 and/or 𝛽=1.

Figure 2. Percentage normalized square error (NSE) of the proposed FTBT model, and each of the literature models of Table 2 for the diffusion-weighted acquisition simulations with various 𝜆. Note that the larger the values of the asymmetry unitless parameter 𝜆, the more sub-diffusive is the simulated medium (𝛼/𝛽<1). The proposed FTBT model achieves lower NSE for all 𝜆 than the other models capturing better the sub-diffusivity properties. Further, its NSE is also stable indicating its good performance on sub-diffusive mediums.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

4398