4395
Impact of brain and head and neck radiotherapy fixation and coil configuration on tensor-valued dMRI1Dept. of Translational Medicine, Division of Medical Radiation Physics, Lund University, Lund, Sweden, 2Dept. of Clinical Sciences, Division of Radiology, Lund University, Lund, Sweden, 3Dept. of Hematology, Oncology and Radiation Sciences, Lund University, Lund, Sweden, 4MR Applied Science Laboratory Europe, GE Healthcare, Stockholm, Sweden, 5Diagnostic Radiology, Clinical Sciences, Lund University, Lund, Sweden, 6Lund University Bioimaging Center, Lund University, Lund, Sweden, 7Lund University, Lund, Sweden, 8Brigham and Women's Hospital, Boston, MA, United States
Synopsis
Brain and head and neck cancer patients need fixation while undergoing radiotherapy, which prevents the use of a dedicated head coil when imaging patients using MRI in radiotherapy setup. We investigate the impact of coil setup on the technical feasibility of tensor-valued diffusion MRI in a radiation therapy setting. Three coil configurations were evaluated with respect to SNR and parameter bias in the resulting parametric maps using Bland-Altman plots. As expected, the coils configured for radiation therapy imposed a penalty on the SNR, but accuracy was not negatively impacted.
Introduction
Using diffusion MRI (dMRI) for early treatment response prediction in patients with brain tumors has been an active research field for over 20 years [1,2], so far, with limited clinical impact. Novel diffusion measurement techniques allow a more detailed description of the underlying tissue microstructure. Tensor-valued diffusion encoding can be used to separate effects of microscopic anisotropy, orientation dispersion, and isotropic kurtosis [3] with potential applications in both neurological disorders and tumour imaging [4], including response assessment. For treatment response assessment, it is desirable to utilize existing clinical workflows for radiotherapy planning and follow-up. For brain and head and neck tumors, this often includes a fixation mask, which prevents the use of dedicated head coils during MRI. Instead, flexible surface coils are placed outside the fixation mask, and are combined with a posterior coil in the couch. This setup has fewer coil elements, increased average distance to the object, and sub-optimal coverage of the patient anatomy. The aim of this work is to investigate the impact of coil configurations adapted to radiotherapy of the brain on tensor-valued dMRI. This is done with respect to repeatability across coil configurations in a healthy volunteer.Methods
A healthy subject was scanned on a GE Discovery 750w 3.0T (General Electric, WI, US) with a with a spin-echo sequence capable of tensor-valued diffusion encoding, supplied by the vendor, using TE=124 ms, TR=6364 ms, 2x2x4 mm3 resolution, FOV=240x240x80 mm3, acc=2, scan time 8:42 min, b-values: 0.1, 0.7, 1.4, 2.0 ms/µm2 using 6, 6, 10, 21 linear tensor encoding (LTE) directions. Spherical tensor encoding (STE) was repeated 6, 6, 10, 15 times. A 32-channel head coil, 24-channel head and neck coil and a 6-channel flex coil+posterior array radiotherapy (RT) setup (see fig. 1) were compared under repeatability conditions.QTI enables analysis of tensor-valued dMRI data, and the representation can be simplified in a powder averaged case, according to [4,5,6]:
$$
S(b, b_\Delta) = \exp\left(-b\textrm{MD} + b^2 \textrm{MD}^2\textrm{MK}_{\textrm{I}}/6 + b_\Delta^2 b^2 \textrm{MD}^2\textrm{MK}_{\textrm{A}}/6\right)
$$
where MD is the mean diffusivity, MKA is the anisotropic kurtosis, MKI is the isotropic kurtosis, b is the diffusion weighting, and $$$b_\Delta$$$ is the anisotropy of the b-tensor. STE and LTE correspond to $$$b_\Delta$$$ = 0 and 1, respectively.
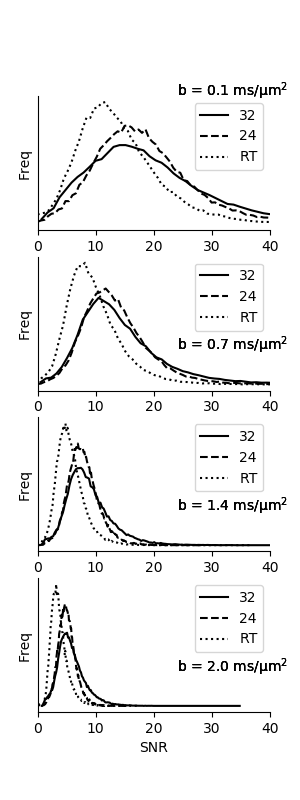
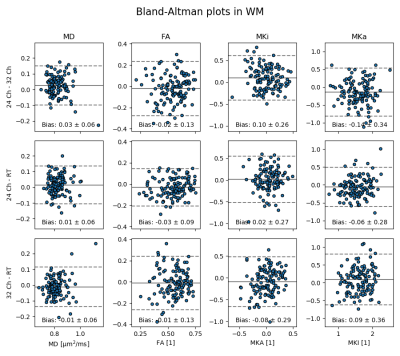
Fitting was done with the MD-dMRI framework [7], and all data was corrected for Gibbs ringing using subvoxel-shifts. Bland-Altman plots were created to show parameter map agreement between set-ups. Voxelwise SNR was calculated for each b-value from STE measurements to gauge bias due to the noise floor. Signal that follow the Rician distribution will begin to suffer from bias when SNR < 3 [8].
Results
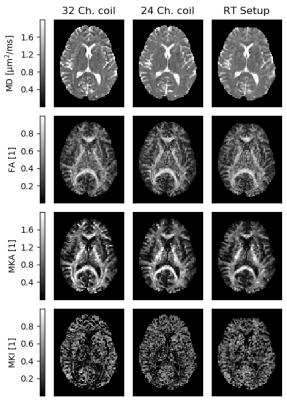
Fig. 2 shows that parameter maps are qualitatively similar, and Bland-Altman plots of a white matter ROI show quantitative agreement across coil configurations with negligible parameter bias (Fig. 3). SNR was on average for all b-values 53% and 27% higher on the 32 and 24 channel set-up respectively, compared to the RT setup (Fig. 4), and was generally above 3 for all b-values apart from the RT coil at the maximal b-value (SNR=3.8±1.4). Prevalence of SNR>3 was 93%, 93% and 68% at b = 2.0 ms/µm2, for the 32-ch., 24-ch. and the RT setup, respectively.Discussion and conclusions
As expected, the RT coil impacted data quality, such that approximately 33% of the brain volume may suffer signal bias due to the noise floor. This effect can be remedied by adopting a 3x3x3 mm3 resolution, which would compensate for the loss in performance. We note that the impact is primarily on MKI, which is observed to be most sensitive to noise, in agreement with previous studies [9]. In summary, we have presented a quantitative analysis that supports the use of tensor-valued encoding and QTI analysis in the context of radiotherapy, using flex-coils in a representative geometry.Acknowledgements
We would like to thank GE (General Electric, WI, US) for supplying the pulse sequenceReferences
[1] Ross, B. D. et al. (1994). Magnetic Resonance Imaging and Spectroscopy: Application to Experimental Neuro-Oncology. Quarterly of Magnetic Resonance in Biology and Medicine, 1(2), 89–106.
[2] Moffat, B. et al. (2006). The functional diffusion map: an imaging biomarker for the early prediction of cancer treatment outcome. Neoplasia, 8(4)
[3] Cory, D. G. at al (1990). Applications of Spin Transport as a Probe of Local Geometry. Abstracts of Papers of the AmericanChemical Society, 199, 105.
[4] Szczepankiewicz F et al. (2016) The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density bydiffusional variance decomposition (DIVIDE). Neuroimage. 142:522-532.
[5] Lasiĉ, S. et al. (2014). Microanisotropy imaging: quantification of microscopic diffusionanisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2, 11.
[6] Westin et al. (2016). Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 135, 345-62.
[7] Nilsson et al.(2018). An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. Proc. Intl. Soc. Mag. Reson. Med. (26), Paris, France.
[8] Gudbjartsson, H. et al. (1995). The Rician distribution of noisy mri data. Magnetic Resonance in Medicine, 34(6), 910–914
[9] Szczepankiewicz et al. (2019). Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PLoS ONE, 14(3), 1–20.
Figures