Introduction

Segmenting the brain into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) is an important task in medical image analysis. Most brain segmentation methods are performed on structural (T1-weighted) MR images. Recently, brain segmentation based on diffusion weighted imaging (DWI) has attracted research interest ^1-2. Many of the algorithms use the diffusion tensor information derived from the DWI signals rather than the signal itself. Only few studies use the original DWI signal to improve the segmentation performance ^3-4. In this paper, we propose to learn sparse representation of DWI images for fully automated segmentation of brain tissues. Inherent characteristics of diffusion weighted signals are derived by dictionary learning in our work. The learned dictionary atoms are automatically clustered into CSF/WM/GM types, which are used to further classify the brain voxels. The proposed method was evaluated on three HCP subjects and achieved good agreement with the segmentation of structural images.

Methods

Data: The datasets of three subjects of the Human Connectome Project (HCP) were tested in our experiments. Each dataset has 288 pre-processed DWI images with isotropic resolution of 1.25 mm, which includes 18 b0 images and three shells of 90 diffusion weighted images with b-values of [1000, 2000, 3000] s/mm². Additional processing includes MPPCA-based denoising, and taking logarithm of the original signal.
Sparse representation theory: Given a set of samples Y = [y₁,y₂,...,y_N] ∈ ℝ^t×N, where t is the length of samples and N is the number of samples, the sparse coding learns a dictionary with M atoms (where the dictionary size is M), D = [d₁,d₂,...,d_M] ∈ ℝ^t×M, and sparse coefficients X, X = [x₁,x₂,...,x_N] ∈ ℝ^M×N, that the samples can be represented as a sparse and linear combination of dictionary atoms:
$$Y ≈ DX. $$
The optimal solution for the above sparse approximation problem is the one that minimizes the ℓ₂-norm representation error with the constraint of coefficients sparsity, which can be the ℓ₁-norm of coefficients. Thus, the objective function of the sparse approximation problem can be formulated as:
$$min_{D,X}\sum_{i=1}^N(||y_{i}-Dx_{i}||_{2}^{2}+{\gamma}S_{norm}||x_{i}||_{1}), $$
where S_norm is the averaged DWI signal norm and γ is a regularization parameter. In our experiments, we adopted the online dictionary learning library (http://spams-devel.gforge.inria.fr/), which provides high efficiency with low computational cost. The atoms are classified into CSF/WM/GM atoms by K-means clustering based on the variance of the atom signal at b=1000 s/mm². The probability of each voxel belonging to a class is computed based on the sum of coefficients of atoms in the class.
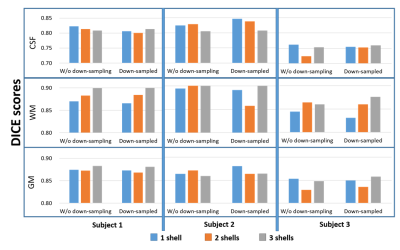
Parameter optimization: Each dataset has a T1-weighted image transformed to the diffusion image space and with the same resolution. The segmentation results are evaluated using the DICE score against the segmentation result using the T1-weighted image in SPM12. To find the optimal value of dictionary size M and the regularization parameter γ for best segmentation performance in general, the DWI datasets were down-sampled in number of shells and number of gradient directions ([3->2->1] × [90 ->30]). Then we applied sparse coding segmentation on all these datasets by varying dictionary sizes from 10-40 atoms with the increment of 5 atoms, and γ =[0.05:0.05:1]. For each dataset, the DICE score using different combination of M and γ was compared against the best one. It turned out that 15 atoms and the regularization parameter γ of 0.3 produce best segmentation results in overall and the performance is not sensitive to γ when learning a dictionary with 15 or 20 atoms.

Results

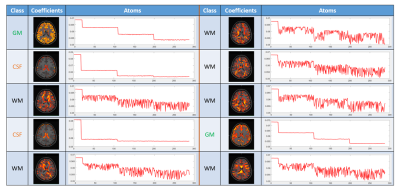
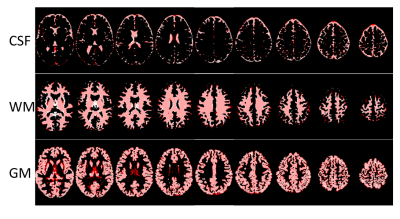
The segmentation takes less than 1 minute for each DWI dataset using matlab. An example of learned atoms and corresponding coefficient maps from a dictionary with size of 10 are shown in Figure 1. The dictionary atoms exhibit inherent features of DWI signals, which are distinct between GM, WM, and CSF. There are six WM atoms, two GM atoms, and two CSF atoms. The CSF atoms have the largest signal drop from b=0 to b=1000 s/mm². The WM atoms are very sensitive to gradient directions, while the variation of GM atoms and CSF atoms with gradient direction is much smaller. Figure 2 shows the segmentation of GM, WM, and CSF of a HCP subject using our proposed method along with the segmentation of the T1-weighted image. The two segmentations match very well except some mismatches at the edges. The averaged DICE score of the three subjects is 0.7889 for CSF, 0.8897 for WM, and 0.8633 for GM, better than the results obtained by Yap et al. (0.6985, 0.8603, 0.8105, respectively) on HCP subjects ⁴. The DICE scores of different DWI data in the parameter optimization experiment are shown in Fig. 3. The DICE scores are all higher than 0.82 for GM and WM in these three subjects. The performance is not sensitive to the number of shells or down-sampling, which means good segmentation can be achieved with only 30 directions of one shell.

Conclusion

We developed an automated brain tissue segmentation method using sparse representation of DWI signals. Segmentation of CSF/WM/GM using DWI images with our proposed method achieved good agreement with the segmentation from T1-weighted images. The proposed brain segmentation method is robust to number of DWI shells and gradient directions.

Acknowledgements

No acknowledgement found.