4377
Joint Sparsity and Low Rankness-based Spectroscopy Reconstruction for Magnetic Resonance Diffusion-Ordered NMR1School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China, 2School of Opto-Electronic and Communication Engineering, Xiamen University of Technology, Xiamen, China, 3Department of Electronic Science, Xiamen University, Xiamen, China
Synopsis
The magnetic resonance diffusion ordering spectrum has been widely used in the separation of mixture due to the mobility of molecular self-diffusion reaction molecules. We propose a hybrid time and exponential decay signal recovery method based on low rank Hankel matrix1 to accelerate the acquisition. The experimental results show that this method enables to reduce the error between the recovery diffusion spectrum and the fully sampled signal, and enhance the peak intensity.
Purpose
The magnetic resonance diffusion ordering spectrum serves as one of the important means to detect and analyze the chemical components2, 3 from the mixture without invasion. However, the long acquisition time limits the spread of applications4, which motivates the need of Non-Uniform Sapling (NUS) and reconstruction method. Although iterative thresholding algorithm for multiexponential decay (ITAMeD) based on the sparsity of the diffusion spectral plane, which is proposed 5, in the case of relatively strong noise, more pseudo peaks will be observed6. In this work, we introduce low rank Hankel matrix7-9 into the constrain, and propose a new method to suppress the pseudo peaks and preserve peak intensity.Method
The mathematical model of the hybrid gradient and exponential decay signal is formulated as $$ X\left( {t,b} \right) = \sum\limits_{i = 1}^I {{x_i}\left( t \right) \otimes {s_i}\left( b \right)} ,(1)$$ where $$$ {x_i}\left( t \right) $$$ is one-dimensional time domain signals, $$$ {s_i}\left( b \right) $$$ is exponentially decaying dimensional signal corresponding to the time domain signal, $$$ \otimes $$$ is Kronecker product, and I is the number of time domain signals that correspond to only one exponential decay dimension. The transformation that converting the diffusion spectrum $$$ {\bf{H}} $$$ to the hybrid gradient and exponential decay signal $$$ {\bf{X}} $$$ can be expressed as $$ {{\bf{F}}^{ - 1}} \otimes {\bf{Lh}} = {\bf{x}} ,(2)$$ where $$$ {{\bf{F}}^{ - 1}} $$$ denotes discrete Fourier inverse transformation matrix, $$$ {\bf{L}} $$$ denotes discrete Laplace transform matrix, $$$ {\bf{h}} $$$ and $$$ {\bf{x}} $$$ are the vectorized forms of the diffusion spectrum $$$ {\bf{H}} $$$ and the mixed time-exponential decay signal $$$ {\bf{X}} $$$. The proposed model is formulated as $$ \mathop {\min }\limits_{\bf{h}} \frac{1}{2}\left\| {{{\cal U}{\cal A}}{\bf{h}} - {\bf{x}}} \right\|_2^2 + {\lambda _1}{\left\| {\bf{h}} \right\|_1} + {\lambda _2}\sum\limits_{m = 1}^M {{{\left\| {{{\cal R}}{{{\cal Q}}_m}{{\cal A}}{\bf{h}}} \right\|}_*}} ,(3)$$ where is $$$ {{\cal U}} $$$ undersampling operator, $$$ {{\cal A}} $$$ is Fourier-Laplace joint transformation matrix, $$$ {{\cal A}}{\bf{h}} $$$ stands for vectorized form of the mixed-time dimension-exponential decay dimension signal for recovery. $$$ {{\cal R}} $$$ denotes an operator that constructs a vector as a Hankel matrix, $$$ {{{\cal Q}}_m} $$$ is the operator that extracts the $$$ {m^{th}} $$$ one-dimensional time signal, $$$ {\lambda _1} $$$ and $$$ {\lambda _2} $$$ are regularization parameters. $$$ {\left\| \right\|_*} $$$ represents the kernel norm of a matrix, $$$ {\left\| \right\|_1} $$$ and $$$ {\left\| \right\|_2} $$$ represent the $$$ {l_1} $$$ and $$$ {l_2} $$$ norm, respectively.Result
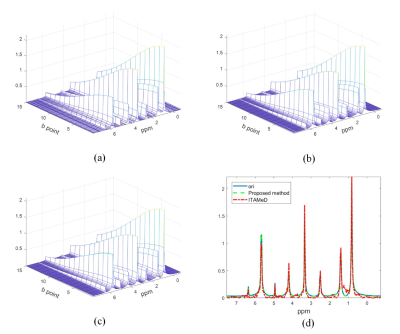
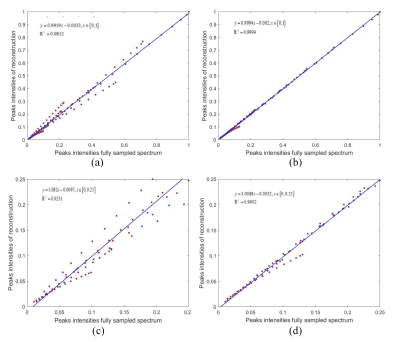
In order to verify the performance, the proposed method is tested on a real two-dimensional diffusion magnetic resonance data, and compared with ITAMeD. The sample solvent is deuterated dimethyl sulfoxide (DMSO-d6), the solute is n-propanol (C3H7OH), dihydrofuran (C4H6O), dichloromethane (CH2CL2), and the instrument used for sampling the diffusion experimental data is Varian 500Mhz magnetic resonance spectrometer. The reconstruction results have been shown in Figure 1. In order to present the performance for peak intensity, a 1D slice is selected. It is clear that the proposed method is closer to the fully sampled signal, especially in the peak at 5.7 ppm(Figure 1(d)). Besides, the baseline of the proposed method owns less oscillation. The correlation results of the two methods presented in Figure 2 also demonstrate that the proposed method owns better performance in peak intensity, including the small peak.Conclusion
A hybrid time-exponential-attenuation-dimensional signal recovery method is proposed based on low rank Hankel matrix, which focuses on the recovery of the mixed signal itself. In this work, the low rank Hankel matrix constraint is introduced, and combine with the sparsity of the mixed signal. The experiment on real data shows that, comparing with the state-of-the-art method, ITAMeD, the proposed method, the proposed method can recover the high-fidelity mixed signal from a small amount of sampled data, including the more accurate peak intensity and the better line-shape.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (61871341, 61971361, 61571380, 61811530021, U1632274), the National Key R&D Program of China (2017YFC0108703), the Natural Science Foundation of Fujian Province of China (2018J06018), the Fundamental Research Funds for the Central Universities (20720180056), and the Science and Technology Program of Xiamen (3502Z20183053) .
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
1. X. Qu, M. Mayzel, J.-F Cai, Z. Chen, V. Orekhov. Accelerated NMR spectroscopy with low-rank reconstruction, Angewandte Chemie International Edition, vol. 54, no.3, 852-854, 2015.
2. M. Betz, K. Saxena, and H. Schwalbe, "Biomolecular NMR: a chaperone to drug discovery," Current Opinion in Chemical Biology, vol. 10, pp. 219-225, 2006.
3. A. Cavalli, X. Salvatella, C. M. Dobson, and M. Vendruscolo, "Protein structure determination from NMR chemical shifts," Proceedings of the National Academy of Sciences, vol. 104, pp. 9615-9620, 2007.
4. J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde factorization of Hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy," IEEE Transactions on Signal Processing, vol. 66, pp. 5520-5533, 2018.
5. M. Urbańczyk, D. Bernin, W. Koźmiński, and K. Kazimierczuk, "Iterative thresholding algorithm for multiexponential decay applied to PGSE NMR data," Analytical Chemistry, vol. 85, pp. 1828-1833, 2013.
6. H. M. Nguyen, X. Peng, M. N. Do, and Z.-P. Liang, "Denoising MR spectroscopic imaging data with low-rank approximations," IEEE Transactions on Biomedical Engineering, vol. 60, pp. 78-89, 2012.
7. H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, et al., "Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy," IEEE Transactions on Biomedical Engineering, vol. 65, pp. 809-820, 2017.
8. J. Ying, H. Lu, Q. Wei, J.-F. Cai, D. Guo, J. Wu, et al., "Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals," IEEE Transactions on Signal Processing, vol. 65, pp. 3702-3717, 2017.
9. X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, V. Orekhov, and Z. Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angewandte Chemie International Edition, 2019. DOI:10.1002/anie.201908162.
Figures