4372
Concomitant Gradient Field Corrections for Asymmetric Diffusion Encoding Waveforms
Matthew J. Middione1, Michael Loecher1, Kévin Moulin1,2, and Daniel B. Ennis1,2,3
1Department of Radiology, Stanford University, Palo Alto, CA, United States, 2Cardiovascular Institute, Stanford University, Palo Alto, CA, United States, 3Veterans Administration Health Care System, Division of Radiology, Palo Alto, CA, United States
1Department of Radiology, Stanford University, Palo Alto, CA, United States, 2Cardiovascular Institute, Stanford University, Palo Alto, CA, United States, 3Veterans Administration Health Care System, Division of Radiology, Palo Alto, CA, United States
Synopsis
In DWI, applied diffusion gradients are assumed to be linear in space, but in practice are accompanied by additional undesired concomitant gradient (CG) fields that arise as a consequence of Maxwell’s equations. These CG fields contribute a residual gradient moment for asymmetric diffusion encoding strategies, which may impact the quantitative accuracy of the measured ADC. In this work, a CG correction method that does not increase the minimum achievable TE was implemented for clinically relevant asymmetric diffusion encoding DWI protocols and the mean ADC error reduction was characterized.
Introduction
Diffusion-weighted MRI (DWI) uses strong magnetic field gradients to encode the diffusion of water. Conventional methods of diffusion encoding, such as Stejskal‐Tanner1, use symmetric monopolar gradient waveforms on either side of a refocusing RF pulse. The applied diffusion gradients are assumed to be linear in space, but Maxwell’s equations dictate that whenever a linear magnetic field gradient is applied, accompanying spatially dependent concomitant gradient (CG) fields are present2. These CG fields contribute a residual non-zero gradient moment that leads to intravoxel phase dispersion and may impact the quantitative accuracy of the apparent diffusion coefficient (ADC). Conventional symmetric diffusion encoding strategies ensure that the effects of CG fields from each lobe are self-cancelling. More recently, DWI methods have incorporated asymmetric diffusion encoding strategies that encode the same b-value in a shorter TE3-8. While these methods improve SNR due to the reduced TE, the asymmetry does not ensure cancellation of CG fields. Optimization methods have been proposed to incorporate a CG field constraint to ensure cancellation of the effect7-9, but these methods can have long compute times and/or significantly increase the minimum achievable TE.One CG field correction strategy calculates the CG fields at a specific location in space and then compensates the applied waveform(s)10,11 using “gradient lifting”, which lifts the gradient amplitude such that the ensuing CG fields will be nullified. Gradient lifting corrects the CG field error at a single pixel location, but data acquired distant from this location may still be affected by residual CG fields or made worse by the gradient lifting. To the best of our knowledge, no formal analysis has been conducted to define which pixel location to select for prospective CG field correction for asymmetric diffusion encoding strategies.
In this work, a CG correction method that does not increase the minimum achievable TE was implemented for clinically relevant asymmetric diffusion encoding DWI protocols and the mean ADC error reduction was characterized.
Methods
CG fields ($$$G_{c}$$$) can be approximated at a given $$$(x,y,z)$$$ position using a second-order Taylor series expansion2:$$G_{c}(x,y,z,t)\approx \frac{1}{4B_{0}}\left[{\begin{matrix}G_{z}^2(t)&0&-2G_{x}(t)G_{z}(t)\\0&G_{z}^2(t)&-2G_{y}(t)G_{z}(t)\\-2G_{x}(t)G_{z}(t)&-2G_{y}(t)G_{z}(t)&4G_{x}^2(t)+4G_{y}^2(t)\\\end{matrix}}\right]\left[{\begin{matrix}x\\y\\z\\\end{matrix}}\right]\quad \quad \quad Eq. [1]$$
As per Eq. [1], CG fields can only be corrected at a single pixel location. To identify the location that maximizes the reduction of the CG field effects throughout the entire imaging FOV, numerical simulations were performed for typical cardiac, neuro, and liver DWI protocols (Table 1). Time-optimal asymmetric diffusion gradient waveforms were generated using an open source Gradient Optimization Toolbox (GrOpt, https://github.com/cmr-group/gropt).
A brute force approach was used to analyze the impact of the choice of pixel location on the ability to correct for CG fields. For each of the tested protocols, every pixel location, $$$(x',y',z')$$$, within the imaging FOV was used as input to Eq. [1]. The resulting $$$G_{c}(x,y,z,t,x',y',z')$$$ was used to generate a phase error map, $$$\phi(x,y,z,x',y',z')$$$, calculated by taking the product of the residual zeroth gradient moment along each axis and the pixel location. The pixel location that, on average, minimized the mean phase error across all slices was then identified as the optimal pixel location for CG field correction. ADC maps were generated for each protocol using the optimal pixel input and Eqs. [2-3] with 81 simulated spins per voxel (j=81):
$$S_{D}(x,y,z)=\sum_{j=1}^{81}S_{0}(x,y,z)e^{-bD}e^{-i\phi_{j}(x,y,z)} \quad \quad \quad Eq. [2] \quad \quad \quad D(x,y,z)=\frac{ln(|S_{D}(x,y,z)|/|S_{0}(x,y,z)|)}{-b} \quad \quad \quad Eq. [3]$$
DICOM datasets acquired for each of the three protocols were masked and multiplied by the ADC maps. The mean ADC error across all slices was computed for each protocol as mean(D$$$(x,y,z)$$$).
Results
The brute force method identified a pixel location of $$$(0,0,z)$$$ as the ideal location to use for CG field correction for all axial protocols. Simulated ADC maps for the cardiac (Fig. 1), neuro (Fig. 2), and liver (Fig. 3) protocols are shown before and after CG field correction.Discussion
The gradient lifting CG field correction technique resulted in the mean ADC error across all slices being reduced by ~2.5x (16% vs. 6.4%) for the cardiac protocol (Fig. 1), ~1.75x (16.7% vs. 8.9%) for the neuro protocol (Fig. 2), and ~2.25x (22.4% vs. 9.8%) for the liver protocol without incurring a TE penalty.Although the gradient lifting CG field correction reduces the average ADC error, some pixel locations may have an increased error while others are eliminated. Perfect cancellation of CG fields with asymmetric diffusion encoding strategies can be achieved with a phase symmetry constraint7-9, but these methods increase the TE, which decreases the SNR and can decrease ADC accuracy.
A number of parameters used in these simulations were fixed, such as B0, GMax, scan orientation, and imaging volume size. Errors arising due to CG fields depend on the values chosen for these parameters, but the protocols chosen herein are representative of a subset of clinically relevant imaging volumes.
Conclusion
This work shows that the gradient lifting CG field correction technique using a single pixel location can mitigate the impact of CG fields for asymmetric diffusion encoding strategies such that the ADC error is ≤10%. This work enables the use of time-optimal asymmetric diffusion encoding strategies, without the need to constrain for CG fields and unnecessarily increasing the minimum achievable TE.Acknowledgements
This project was supported, in part, by NIH R01 HL131823 to DBE.References
- Bernstein MA, et al. Concomitant gradient terms in phase contrast MR: analysis and correction. Magn Reson Med. 1998;39:300–308.
- Stejskal EO, Tanner JE. Spin diffusion measurement: spin echoes in the presence of a time‐dependent field gradient. J Chem Phys. 1965;42:288–292.
- Aliotta et al. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion compensated diffusion weighted MRI. Magn Reson Med 2017;77:717–729.
- Aliotta et al. Eddy current–nulled Convex Optimized Diffusion Encoding (EN-CODE) for distortion-free diffusion tensor imaging with short echo times. Magn Reson Med 2018;79:663–672.
- Sjölund et al. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157-168.
- Shrestha M, et al. Optimization of diffusion-weighted single-refocused spin-echo EPI by reducing eddy-current artifacts and shortening the echo time. Magn Reson Mat in Phys, Bio and Med. 2018;31.5:585-597.
- Yang et al. Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms. Magn Reson Med 2018;00:1–15.
- Peña‐Nogales Ó, et al. Optimized Diffusion‐Weighting Gradient Waveform Design (ODGD) formulation for motion compensation and concomitant gradient nulling. Magn Reson Med. 2019;81.2:989-1003.
- Szczepankiewicz F, et al. Maxwell‐compensated design of asymmetric gradient waveforms for tensor‐valued diffusion encoding. Magn Reson Med. 2019;82(4):1424-1437.
- Baron CA, et al. The effect of concomitant gradient fields on diffusion tensor imaging. Magn Reson Med. 2012;68:1190–1201.
- Meier C, et al. Concomitant field terms for asymmetric gradient coils: consequences for diffusion, flow, and echo‐planar imaging. Magn Reson Med. 2008;60:128–134.
Figures
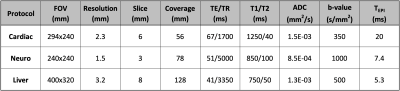
Table 1. Protocol parameters used for the
numerical simulations. All protocols used B0=3T, maximum gradient
amplitude=58mT/m, maximum slew rate= 100mT/m/ms, 2x parallel imaging, RF
durations of 2.4ms and 5.1ms for the excitation and refocusing pulses,
respectively, axial slices, and applied diffusion gradients along x, y, and z
concurrently. The
neuro and liver protocols used partial Fourier, while the cardiac protocol
did not. The T1, T2, and ADC values were chosen to represent that of
myocardium (cardiac), white matter (neuro), and healthy
liver tissue (liver).

Figure 1. Simulated ADC
maps for the cardiac protocol (A) before and (B) after the
proposed concomitant gradient field correction shown for five slices at
different z-locations from isocenter, including the two volumes most distant
from isocenter. The mean absolute ADC error across all slices was reduced from (A) 16.0% to (B) 6.5%. The simulated ADC value was 1.5x10-3mm2/s.
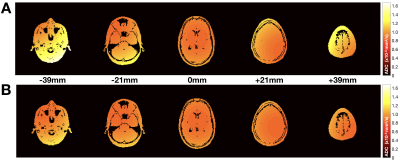
Figure 2. Simulated
ADC maps for the neuro protocol (A) before and (B) after the
proposed concomitant gradient field correction shown for five slices at
different z-locations from isocenter, including the two volumes most distant
from isocenter. The mean absolute ADC error across all slices was reduced from (A)
16.7% to (B) 8.9%. The simulated ADC value was 0.85x10-3mm2/s.

Figure 3. Simulated
ADC maps for the liver protocol (A) before and (B) after the
proposed concomitant gradient field correction shown for five slices at
different z-locations from isocenter, including the two volumes most distant
from isocenter. The mean absolute ADC error across all slices was reduced from (A) 22.4% to (B) 9.8%. The simulated ADC value was 1.3x10-3mm2/s.