4369
Whole-brain in-vivo submillimeter diffusion MRI in 10 minutes with combined gSlider-Spherical Ridgelets reconstruction1Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States, 2Massachusetts General Hospital, Harvard Medical School, Charlestown, MA, United States, 3University of Waterloo, Waterloo, ON, Canada
Synopsis
gSlider is an efficient, super-resolution, technique to achieve submillimeter diffusion MRI data circumventing the trade-off between image resolution and SNR. Yet, the long acquisition time is still an issue. In this work, we extend gSlider by allowing under-sampling both in q-space and Radio-Frequency (RF)-encoded data, achieving then shorter acquisition time that gSlider. Our method, gSlider-SR, uses a basis of Spherical-Ridgelets to exploit the redundancy of the dMRI data, while at the same time enhancing SNR. We demonstrate that only ten minutes are needed to reconstruct 64 diffusion directions (b=2000s/mm2) at 860 μm data with reliably signal preservation.
Introduction
Submillimeter diffusion MRI (dMRI) can provide anatomical maps of the human brain at unprecedented level of detail. At that resolution, very low SNR is a serious concern. To circumvent it, super-resolution methods in dMRI such as gSlider have shown great promise. Unfortunately, dMRI data acquired with gSlider1 yet requires a long acquisition time to increase SNR (by means of averaging). In this work, we combine the conventional gSlider with Spherical Ridgelets2-5 an overcomplete basis for dMRI signal that promotes sparsity and enables high SNR image reconstruction with undersampled q-space schemes, thereby accelerating the total acquisition time.Methods
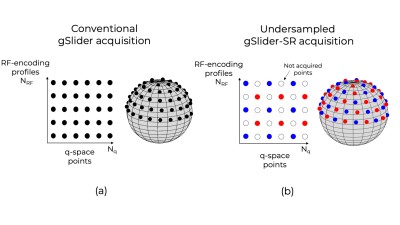
gSlider Spherical Ridgelets (gSlider-SR) reconstructionIn a conventional gSlider acquisition protocol1, the super-resolution dMR data of $$$N_q$$$ q-space points, $$${\bf{S}} \in \mathbb{R}^{N \times N_q}$$$, ($$$N$$$ is the number of voxels) is related to the $$$N_{RF}$$$ acquired, real, phase-corrected, thick-slices DWI data $$${\bf{Y}}_k \in \mathbb{R}^{N_{low} \times N_q} $$$, ( $$$N$$$ is the number of voxels) as
$${\bf{Y}}_k = {{\bf A}_k}{\bf{S}} + {\boldsymbol{\eta}}_k, \; \; k=1,..., {N_{RF}} \;[1]$$
where $$${\bf{A}}_k \in \mathbb{R}^{N_{low} \times N}$$$ is the down-sampling operator (along the slice direction) of the $$$k-th$$$ RF-encoding gSlider basis1 and $$${\boldsymbol{\eta}}_k \in \mathbb{R}^{N_{low} \times N_{q}}$$$ is Gaussian noise. If the slice thickness of $$${\bf{Y}}_k$$$ are $$$N_{RF}$$$ times bigger than the thin-slices, recovering $$$\bf S $$$ in [1] is well-posed and can be done with a Tikhonov-based linear least squares (LLS) reconstruction with at least $$$N_{RF}N_{q}$$$ DWI (Fig1a). Multiple averages ($$$N_{scan}$$$) are typically needed to improve the low SNR making the total acquisition time infeasible for clinical research studies.
In this work, we propose (gSlider-SR) to use only interleaved samples by undersampling in both q and RF-space (Fig1b) to reduce the total number of DWI images needed, thereby reducing the acquisition time. Each diffusion direction is probed not with all $$$k=1,...,N_{RF}$$$ encoding profiles but with a subset of them:
$${\bf{Y}}_k = {{\bf A}_k}{\bf{S}}{{\bf Ω}_k}+ {\boldsymbol{\eta}}_k, \;[2]$$
where $$${{\bf Ω}_k}$$$ is a q-space sampling mask. Recovering $$$\bf S$$$ is an ill-posed problem that we solve using the Spherical Ridgelets sparse basis used successfully in our compressed-sensing framework2-5 . We look for the coefficients of the SR-basis that are sparse with the corresponding $$$\bf S$$$ that adheres to the forward model in [2]. In addition to allowing under sampling schemes, SR enhances the SNR so multiples averages $$$N_{scan}$$$ are unnecessary.
Experiments
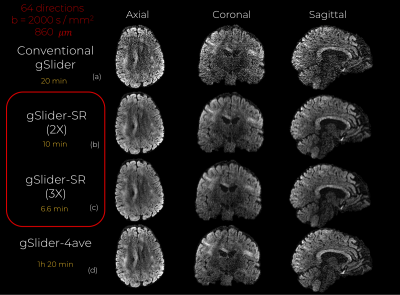
We validated gSlider-SR with in-vivo human brain data. Whole-brain gSlider-SMS dMRI data with 860 micrometer in-plane resolution, 64 diffusion directions ($$$b = 2000 s / {mm}^2$$$) and 8 b0 were acquired (axially). Other parameters were: slice thickness = 4.3 mm, $$$N_{RF}$$$ =5, MB=2, $$$R_{in-plane} = 3$$$. Total acq time = 20 min. $$$N_{scan} = 4$$$ scans were acquired of the same subject. Background phase correction was applied to get real thick-slice data, thereby making noise Gaussian6. Data were reconstructed with (a) conventional gSlider and (b) gSlider-SR. For gSlider-SR, we applied undersampling in q-space by a factor of 2X (32 diffusion directions per RF-encoding). ). We also get preliminary results with an acceleration factor of 3X (22 directions). We compare gSlider-SR with the average of the 4 scans reconstructed with gSlider (gSlider-4av). All reconstructed DWI sets were registered (affine transformation) to a reference b0 image to account for eddy current distortion and head motion. gSlider-SR incorporated such a registration step iteratively.
Results
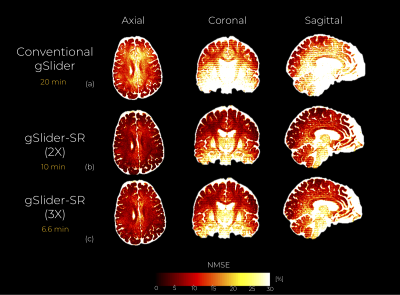
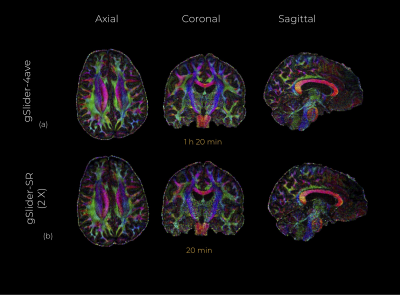
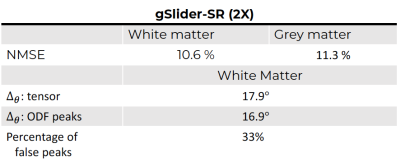
An axial, coronal and sagittal slice of the same DWI are shown in Fig.2 for conventional gSlider and gSlider-SR. Notice that, despite using an incomplete set of RF-encoding basis, gSlider-SR is able to reconstruct good quality image, which preserves information compared to the original fully-sampled image. Note also the SNR-enhancing capability of gSlider-SR (comparable to gSlider-4 av but eight times faster) due to the high-frequency noise-reducing characteristics of the SR basis, in comparison to gSlider. Many details that were obscured by noise in conventional gSlider are well-preserved and delineated with gSlider-SR. Normalized mean square error (NMSE) maps (Fig.3) indicates a reliable signal reconstruction, with low errors in both white and gray matter. Color-encoded FA of gSlider-SR (2X) is displayed in Fig. 4b, showing the fine anatomical details similar to gSlider-4av. Finally, quantitative results (gSlider-SR 2X) reported in Fig5 indicate good performance, with lower errors than others methods in the literature7Discussion
In this work, we show that with synergistic undersampling in q and RF-encoding space, we can accelerate the total acquisition time of conventional gSlider while boosting SNR. The ability to reconstruct a high-quality, super-resolution data in this ill-posed scenario comes from the power of spherical ridgelets, a sparse basis for representing the dMRI signal that provides the theoretical guarantees for exact recovery in a compressed-sensing framework. Furthermore, spherical ridgelets allows to increase SNR, skipping multiple averaging for denoising. Finally, gSlider-SR allows multiple extensions that can boost its performance. We anticipate superior results if low-rank denoising8,9 is integrated into the gSlider-SR framework, as well as if motion between thick-slices is estimated simultaneously10,11.Conclusion
We introduced an integrated and accelerated gSlider-SR reconstruction framework for whole-brain high angular resolution dMRI at submillimeter spatial resolution in clinically feasible acquisition time. Here, we demonstrate comparable quality to fully-sampled gSlider with four averages (64 directions $$$b=2000 s/{mm}^2$$$) at 860 micrometer) in 10 minutes instead of 1 h 20 min.Acknowledgements
R01MH116173 (PIs: Setsompop, Rathi)References
1. Setsompop, K., Fan, Q., Stockmann, J., Bilgic, B., Huang, S., Cauley, S. F., ... & Wald, L. L. (2018). High‐resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (g Slider‐SMS). Magnetic resonance in medicine, 79(1), 141-151.
2. Michailovich, O., & Rathi, Y. (2009). On approximation of orientation distributions by means of spherical ridgelets. IEEE Transactions on Image Processing, 19(2), 461-477.
3. Michailovich, Oleg, Yogesh Rathi, and Sudipto Dolui. "Spatially regularized compressed sensing for high angular resolution diffusion imaging." IEEE transactions on medical imaging 30.5 (2011): 1100-1115.
4. Rathi, Y., Michailovich, O., Shenton, M. E., & Bouix, S. (2009). Directional functions for orientation distribution estimation. Medical image analysis, 13(3), 432-444.
5. Ning, L., Setsompop, K., Michailovich, O., Makris, N., Shenton, M. E., Westin, C. F., & Rathi, Y. (2016). A joint compressed-sensing and super-resolution approach for very high-resolution diffusion imaging. NeuroImage, 125, 386-400.
6. Eichner, C., Cauley, S. F., Cohen-Adad, J., Möller, H. E., Turner, R., Setsompop, K., & Wald, L. L. (2015). Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage, 122, 373-384.
7. Wu, W., Koopmans, P. J., Andersson, J. L., & Miller, K. L. (2019). Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER). Magnetic resonance in medicine, 82(1), 107-125
8. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. NeuroImage, 142, 394-406.
9. Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A. N., & Hajnal, J. V. (2019). Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage.
10. Ramos-Llorden, G., Arnold, J., Van Steenkiste, G., Jeurissen, B., Vanhevel, F., Van Audekerke, J., ... & Sijbers, J. (2016). A unified maximum likelihood framework for simultaneous motion and $ T_ {1} $ estimation in quantitative MR $ T_ {1} $ mapping. IEEE transactions on medical imaging, 36(2), 433-446.
11. Fogtmann, M., Seshamani, S., Kroenke, C., Cheng, X., Chapman, T., Wilm, J., ... & Studholme, C. (2013). A unified approach to diffusion direction sensitive slice registration and 3-D DTI reconstruction from moving fetal brain anatomy. IEEE transactions on medical imaging, 33(2), 272-289.
Figures