4365
Fast Simultaneous Multi-Slice Multi-Shell Diffusion Tensor Imaging with Model-based Reconstruction1Institute of Medical Engineering, Technical University Graz, Graz, Austria, 2Institute for Computer Graphics and Vision, Technical University Graz, Graz, Austria, 3Biotechmed, Graz, Austria
Synopsis
Multi-Shell DTI suffers from low SNR for high b-value data and prolonged scan time. The Gaussian noise assumption is typically violated due to multi-coil imaging and magnitude forming thus requiring special treatment to avoid biases in the DTI estimates. To this end, we propose a model-based reconstruction technique to exploit the Gaussian noise in the raw k-space data and enable acceleration of the DTI measurement. We show the acceleration potential and quantitative accuracy of the proposed method for mono- and bi-exponential fitting approaches on freely available DTI data and full brain DTI measurements of one healthy volunteer.
Introduction
Diffusion MRI with multiple diffusion encodings (directions, b-values) requires accelerated imaging techniques for the practical applicability and suffers from poor SNR especially for higher b-values. Proper treatment of the data is required to avoid biases in subsequent analysis. Model-based reconstruction has been shown to allow acceleration of data acquisition beyond conventional parallel imaging techniques1,2,3,4. The reconstruction and fitting is directly performed on the raw measurement data and thus avoids complications from non-Gaussian noise models, in particular for multi-array coils. The validity of the Gaussian noise assumptions is notably important for fitting high b-value data to models such as Kurtosis or bi-exponential based diffusion tensor imaging (DTI). To this end, we propose a novel model-based reconstruction method for DTI to reduce the acquisition time of multi-shell acquisition and overcome non-Gaussian noise based biases in the estimates of the diffusion tensor. Further, we employ a simultaneous multi slice (SMS) diffusion sequence to reduce acquisition time. This combination yields high resolution (2.3 mm3) multi-shell DTI measurements of the whole brain within an acquisition time of 6 min.Methods
For a given diffusion gradient direction $$$\mathbf{g_m}$$$ and strength $$$b_i$$$ the measured k-space signal can be expressed as:$$y_{i,m}(S_0, \mathbf{D})=\mathcal{F}\,CS_0e^{-b_i\mathbf{g_m}^T\mathbf{D}\mathbf{g_m}}$$
where $$$\mathcal{F}$$$ is the Fourier operator including k-space sampling and $$$\mathcal{C}$$$ are the complex coil sensitivity profiles estimated from the data5. $$$S_0$$$ corresponds to no diffusion weighting and $$$\mathbf{D}$$$ is the fully symmetric diffusion tensor, assuming a Gaussian diffusion model. The symmetry property of $$$\mathbf{D}$$$ can be exploited by fitting the elements of the Cholesky decomposition $$$\mathbf{D}^{}=\mathbf{L}^{}\mathbf{L}^T$$$ . This implicitly poses a positive (semi-) definite constraint on $$$\mathbf{D}$$$, justified by the physical properties of DTI. The following optimization task describes the fitting procedure:
$$\underset{x=(S_0,\mathbf{L})}{\min}\,\,\frac{1}{2}\|\sum_{i=1}^{N_b}\sum_{m=1}^{N_g}\mathcal{F}\,CS_0 e^{-i\phi_{i,m}}e^{-b_i \mathbf{g_m}^T\mathbf{L}\mathbf{L}^T\mathbf{g_m}}-y_{i,m}\|_2^2+\lambda{TGV}(x)$$
The minimization of this non-linear problem is implemented using a combination of an iteratively-regularized Gauss-Newton and a primal-dual algorithm6, as recently proposed for quantitative MRI4, solving for $$$S_0$$$ and the six non-zero entries of $$$\mathbf{L}$$$. An additional spatial prior, Total Generalized Variation ($$$TGV$$$)7,8, directly acting on the tensor elements is applied, which has been shown to be superior compared to individually regularizing the DWI images8,10,11. Phase variations $$$\phi_{i,m}$$$ are estimated prior to the optimization using a CG-SENSE based reconstruction of each diffusion weighted acquisition. The implementation of the bi-exponential model12 follows analogously.
Our proposed method is compared to adaptive soft coefficient matching13 using the implementation in DiPy14. For the reference approach the following steps were performed: reconstruction of the DWI using a CG-SENSE based algorithm followed by adaptive soft coefficient matching13 and finally estimation of the diffusion tensor by fitting the DWI series using the supplied tensor fitting routines of DiPy.
The reference data set consists of magnitude images provided by Hansen et al.15. Prospective accelerated measurements were performed on a 3T MR system (Prisma, Siemens Healthcare, Germany) using a single-shot EPI sequence16,17 with 33 diffusion directions15. The acquisition parameters are given in Table 1.
Results and Discussion
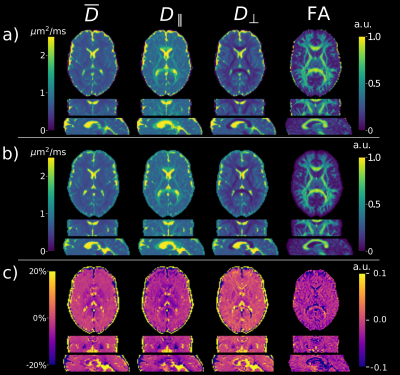
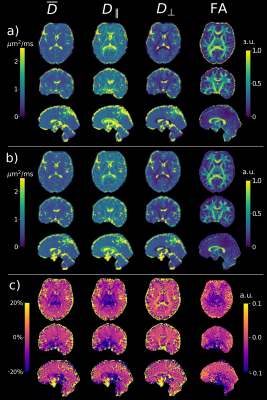
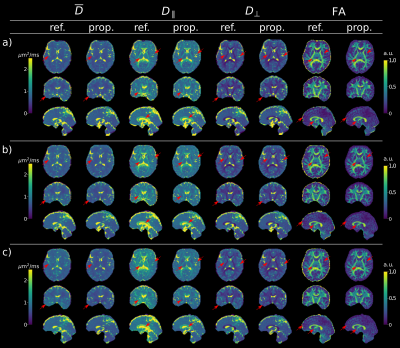
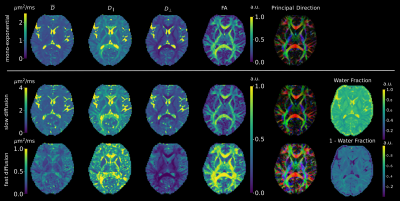
Figure 1 shows that the values produced by the proposed model-based reconstruction are highly comparable to the reference for fully sampled, high SNR data, preserving details without blurring of the tensor estimates. Reconstructions from prospective accelerated in-vivo data show improved visual quality using the proposed method as compared to the reference (Figure 2 and 3) which tends to overestimate tensor values in the central brain region. This may be due to residual coil sensitivity errors and g-factor amplification and becomes even more pronounce with increasing multi-band acceleration factors (Figure 3). Model-based reconstruction compensates these errors and shows reconstructions with only minimal loss of quantitative and visual quality over increasing acceleration (Figure 3). In addition, fine structures are better preserved with the proposed model-based approach (red arrows Figure 3). This excellent detail preservation is particularly visible in the area around the corpus callosum and in the sagittal view of the axial diffusivity. The delineation between CSF and corpus callosum can be difficult in the reference reconstruction as opposed to the proposed method. Increasing errors in the reference reconstruction with increasing acceleration may stem in part from violations of the Gaussian noise assumption in the DWI images. In contrast, model-based reconstruction exploits the raw k-space data which generally has a Gaussian noise distribution. Thus the proposed model-based approach utilizes the correct data similarity measure in form of the L2-norm.To fully explore the acquired multi-shell data we employed a bi-exponential model. Even though bi-exponential fitting typically demands many b-values the tensor reconstructions show visually good estimates for fast and slow diffusion (Figure 4). Contrast for grey and white matter tracts also improves compared to mono-exponential fitting. Clear boundaries between grey and white matter are also visible in the water fraction maps. Principal diffusion direction maps of the tensor estimates for slow and fast exchanging compartments reveal connections not visible in the mono exponential counterpart.
Conclusion
In this study we combined an SMS acquisition with in-plane acceleration and a model-based reconstruction approach to reduce the acquisition time for a multi-shell DTI acquisition of the whole brain down to 6 minutes. The model-based method overcomes the inherent transformation of Gaussian noise in multi-coil magnitude images, typically used for DTI, and thus avoids possible bias in the tensor estimates.Acknowledgements
Oliver Maier is a Recipient of a DOC Fellowship (24966) of the Austrian Academy of Sciences at the Institute for Medical Engineering at TUGraz.
We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan Xp GPU used for this research.
References
1. Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J. Magn. Reson. Imaging 2011;34:420–428. doi: 10.1002/jmri.22634.
2. Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T 1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn. Reson. Med. 2018;79:730–740. doi: 10.1002/mrm.26726.
3. Roeloffs V, Wang X, Sumpf TJ, Untenberger M, Voit D, Frahm J. Model-based reconstruction for T1 mapping using single-shot inversion-recovery radial FLASH. Int. J. Imaging Syst. Technol. 2016;26:254–263. doi: 10.1002/ima.22196.
4. Maier O, Schoormans J, Schloegl M, Strijkers GJ, Lesch A, Benkert T, Block T, Coolen BF, Bredies K, Stollberger R. Rapid T 1 quantification from high resolution 3D data with model‐based reconstruction. Magn. Reson. Med. 2019;81:2072–2089. doi: 10.1002/mrm.27502.
5. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion - Joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008;60:674–682. doi: 10.1002/mrm.21691.
6. Chambolle A, Pock T. A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. J. Math. Imaging Vis. [Internet] 2011;40:120–145. doi: 10.1007/s10851-010-0251-1.
7. Bredies K, Kunisch K, Pock T. Total Generalized Variation. SIAM J. Imaging Sci. 2010;3:492–526. doi: 10.1137/090769521.
8. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011;65:480–491. doi: 10.1002/mrm.22595.
9. Knoll F, Raya JG, Halloran RO, Baete S, Sigmund E, Bammer R, Block T, Otazo R, Sodickson DK. A model-based reconstruction for undersampled radial spin-echo DTI with variational penalties on the diffusion tensor. NMR Biomed. 2015;28:353–366. doi: 10.1002/nbm.3258.
10. Dong Z, Dai E, Wang F, Zhang Z, Ma X, Yuan C, Guo H. Model‐based reconstruction for simultaneous multislice and parallel imaging accelerated multishot diffusion tensor imaging. Med. Phys. 2018;45:3196–3204. doi: 10.1002/mp.12974.
11. Welsh CL, DiBella EVR, Adluru G, Hsu EW. Model-based reconstruction of undersampled diffusion tensor k-space data. Magn. Reson. Med. 2013;70:429–440. doi: 10.1002/mrm.24486.
12. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497-505.
13. Coupé P, Manjón JV, Robles M, Collins DL. Adaptive multiresolution non-local means filter for three-dimensional magnetic resonance image denoising. IET Image Process. 2012;6:558. doi: 10.1049/iet-ipr.2011.0161.
14. Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, Nimmo-Smith I and Dipy Contributors (2014). DIPY, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, vol.8, no.8.
15. Hansen B, Jespersen SN. Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Sci. Data 2016;3:160072. doi: 10.1038/sdata.2016.72.
16. Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn. Reson. Med. 2010;63:1144–1153. doi: 10.1002/mrm.22361.
17. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med. 2012;67:1210–1224. doi: 10.1002/mrm.23097.
Figures