4361

SENSE reconstruction with simultaneous 2D phase correction and channel-wise noise removal (SPECTRE)
Elizabeth Powell1,2, Torben Schneider3, Marco Battiston2, Francesco Grussu2,4, Ahmed Toosy2, Jonathan D Clayden5, and Claudia A. M. Gandini Wheeler-Kingshott2,6,7
1Medical Physics and Biomedical Engineering, University College London, London, United Kingdom, 2NMR Research Unit, Queen Square MS Centre, Department of Neuroinflammation, UCL Queen Square Institute of Neurology, Faculty of Brain Sciences, University College London, London, United Kingdom, 3Philips Healthcare, Guildford, United Kingdom, 4Centre for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom, 5Developmental Imaging and Biophysics Section, Great Ormond Street Institute of Child Health, University College London, London, United Kingdom, 6Department of Brain and Behavioural Sciences, University of Pavia, Pavia, Italy, 7Brain MRI 3T Center, IRCCS Mondino Foundation, Pavia, Italy

Synopsis

Nyquist sampling errors in echo planar imaging (EPI) often require 2D phase correction during reconstruction to remove unwanted ghost artefacts; however, phase corrections can be challenging to translate to high b-value diffusion weighted imaging (DWI) owing to associated noise amplification. We introduce SPECTRE (SENSE with 2D PhasE CorrecTion and channel-wise noise REmoval), and demonstrate that the SNR gains achieved by denoising complex channel data enable robust ghost correction without biasing diffusion parameter estimates.

Introduction

Nyquist ghost artefacts are an inherent component of echo planar imaging (EPI). Minor misalignments between opposing k-space trajectories – which produce the ubiquitous ghost image offset by half the field-of-view (FOV) - are caused by gradient system imperfections, and often require complex 2D phase correction during reconstruction. However, 2D phase-corrected reconstruction approaches are generally limited by increased scan times or noise amplification1. Noise amplification is particularly undesirable in diffusion MRI (dMRI), where the drive for ever higher b-values often means that signals are lost to the noise floor. In this work we demonstrate that denoising complex channel data2 prior to reconstruction using phase error correction with sensitivity encoding (PEC-SENSE3) can mitigate a geometry factor-dependent noise (g-noise) amplification in high b-value dMRI and produce robust Nyquist ghost correction.

Methods

Acquisition
Four healthy volunteers (35±5 years, 1 female) were imaged on a 3T Philips Ingenia CX system using the vendor’s 32-channel headcoil. Multi-shell diffusion weighted (DW) EPI were acquired using TR=5000ms, TE=88ms, SENSE acceleration R=2, no partial Fourier encoding, 2mm3 isotropic resolution, with 9 b=0 and q-space sampling using 30 isotropically distributed directions for b=[1000,2000,3000]s/mm2. Image denoising and reconstruction of k-space data were performed off line using Matlab.

Denoising and reconstruction
Signal decorrelation4 between channels was performed using a covariance matrix estimated from a noise-only region in each coil to ensure noise statistics were independently and identically distributed (iid) Gaussian. Complex channel data were independently denoised using the recently proposed Markchenko-Pastur principal component analysis (MP-PCA)5,6 approach (Fig. 1a): eigendecomposition of local spatial patches of redundant q-space measurements enables the suppression of noise-only eigenvalues, the upper bound of which is determined using random matrix theory. Ghost correction was achieved using a phase error map estimated from the separate reconstruction of odd and even k-space lines prior to a final joint SENSE reconstruction of odd and even lines3 (Fig. 1b). This correction for undesired ghosts can cause an increased g-factor and undesirable noise amplification in low SNR data. Results obtained using the proposed SPECTRE method were compared with standard (no denoising) and magnitude MP-PCA denoised PEC-SENSE reconstructions. SENSE reconstructions without 2D phase error correction were also performed to provide a baseline for both residual Nyquist ghosting and expected noise levels in DWI (Fig. 1c).

Post-processing
All reconstructions were corrected (after denoising) for Gibbs ringing7, susceptibility distortions8,9, eddy current and motion artefacts10, and B1 bias field inhomogeneities8. The diffusion tensor (DT) and diffusion kurtosis tensor (DKT) models were fitted to each dataset using MRtrix311; a maximum of b=1000s/mm2 was used for the DT estimation.

Results

Figs. 2 and 3 show example DWI and parameter maps for all reconstructions. EPI ghosting in SENSE reconstructions was most visible in the b=0 image, and translated into localised biases in parameter estimates. This was most appreciable in the mean diffusivity (MD) and mean kurtosis (MK) maps. Ghost artefacts were well corrected in PEC-SENSE reconstructions, but effects of noise amplification were observed in MK maps derived from standard and magnitude denoised PEC-SENSE reconstructions. Distributions of parameter estimates in white matter (Fig. 4) show that SPECTRE notably reduced this noise bias in the estimated parameter maps: lower values were observed in both MK and fractional anisotropy (FA) estimates across subjects consistent with literature12. An increase in the precision of FA values was also observed in the narrower distributions obtained using SPECTRE. MD values were less susceptible to noise level changes as was previously reported13.

Denoising either magnitude reconstructions or complex channel data improved the accuracy of the DKT model fit (Fig. 5). The normalised root-mean-square-deviation (NRMSD) between the measured and predicted signal in white matter was lowered for both denoising approaches, but were lowest for complex channel denoising.

Discussion

Nyquist ghost correction is important in order to minimise biases in quantitative parameter maps; however, many proposed corrections do not translate well to DWI owing to noise amplification that disproportionately affects high b-value data. We have demonstrated here that performing MP-PCA denoising on complex channel data prior to reconstruction with 2D phase error correction is more effective than after image production, as it makes better use of redundancies present in the data. By operating on complex-valued data, the increase in SNR achieved by denoising individual channel images can be used to enable PEC-SENSE ghost correction without having a major impact on the accuracy of parameter estimates. This is of particular benefit for complex, higher order diffusion models such as DKI, and could help the translation of these techniques into clinical practice.

Conclusions

In this work we demonstrate the applicability of MP-PCA denoising to SENSE-aliased EPI from individual channels, and incorporate it into a 2D phase-corrected reconstruction pipeline to improve data quality and alleviate g-noise amplification. The proposed method could benefit other applications that utilise the EPI readout, such as fMRI and intravoxel incoherent motion (IVIM) imaging.

Acknowledgements

We acknowledge the UCL-UCLH Biomedical Research Centre for ongoing funding, the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 634541, the Engineering and Physical Sciences Research Council (EPSRC EP/R006032/1, M020533/1), Spinal Research (UK), Wings for Life (Austria), Craig H. Neilsen Foundation (USA) (jointly funding the INSPIRED study), Wings for Life (169111), and the UK Multiple Sclerosis Society (grants 892/08 and 77/2017).

References

  1. Powell E, Schneider T, Battiston M, et al. Giving up the ghost: a systematic comparison of 2D phase correction algorithms in multi-shell high angular diffusion weighted imaging. Proc Intl Soc Mag Reson Med. (2019).
  2. Lemberskiy G, Baete S, Veraart J, et a. Achieving sub-mm clinical diffusion MRI resolution by removing noise during reconstruction using random matrix theory. Proc Intl Soc Mag Reson Med. (2019).
  3. Xie VB, Lyu M, Liu Y, et al. Robust EPI Nyquist ghost removal by incorporating phase error correction with sensitivity encoding (PEC-SENSE). Magnetic Resonance in Medicine. 2018;79(2):943–951.
  4. Hansen MS & Kellman P. Image reconstruction: an overview for clinicians. J Magn Reson Imaging. 2015;41(3):573–585.
  5. Veraart J, Novikov DS, Christiaens D, et al. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016;142:394–406.
  6. Veraart J, Fieremans E & Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. 2016;76(5):1582–1593.
  7. Kellner E, Dhital B, Kiselev VG, et al. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med. 2016;76:1574-1581.
  8. Andersson JL, Skare S & Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20:870-888.
  9. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23:208-219.
  10. Andersson JL & Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2015;125:1063-1078.
  11. Veraart J, Sijbers J, Sunaert S, et al. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. NeuroImage. 2013;81:335-346.
  12. Jones DK & Basser PJ. Squashing peanuts and smashing pumpkins: how noise distorts diffusion-weighted MR data. Magn Reson Med. 2004;993:979–993.
  13. Farrell JAD, Landman BA, Jones CK, et al. Effects of SNR on the accuracy and reproducibility of DTI–derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5T. J Magn Reson Imaging. 2007;26(3):756–767.

Figures

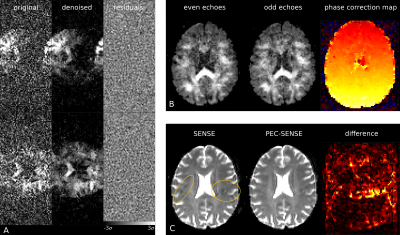
Fig. 1. A. Two representative channels pre- and post-denoising; residuals show no anatomy even in areas of aliased signal. B. After denoising, a phase correction map was generated per EPI volume using the separate reconstructions of odd and even echoes. C. The ghost artefact present in the SENSE reconstruction (left, yellow outline) was corrected in the PEC-SENSE reconstruction. The difference between PEC-SENSE and SENSE reconstructions (bottom right) highlights areas of signal aliasing that were removed by the phase correction.

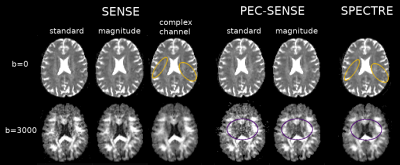
Fig. 2. Ghosting artefacts were visible in the SENSE reconstructions (left, yellow outline), while noise amplification was present at high b-values in the standard and magnitude PEC-SENSE reconstructions (middle, purple outline). Denoising complex channel data during a 2D phase-corrected reconstruction both mitigated ghosting artefacts (right, yellow outline) and limited noise propagation (right, purple outline). Note the noise-floor was also significantly reduced in complex channel denoised data (CSF in purple outlined region, right).

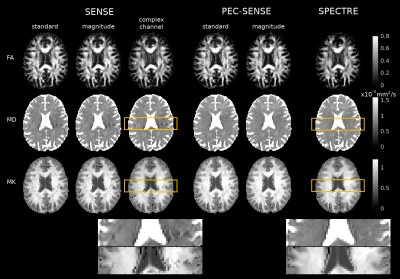
Fig. 3. Residual ghosting in SENSE reconstructions introduced appreciable local biases into MD and MK maps (left, yellow zoomed regions). Phase correction in PEC-SENSE removed biases from ghosting (right, yellow zoomed regions); however, MK estimates in standard and magnitude denoised PEC-SENSE reconstructions appeared inflated on visual inspection. These noise-related biases in MK were less apparent in SPECTRE.

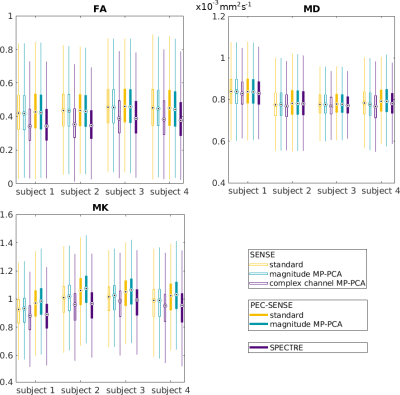
Fig. 4. The distribution of FA estimates in white matter was reduced across all subjects using both SPECTRE and complex channel denoising prior to SENSE owing to improved noise suppression. Noise amplification at higher b-values in standard and magnitude denoised PEC-SENSE was observed in the over-estimation of MK values, which was removed in SPECTRE by denoising complex channel data prior to phase error correction and reconstruction.

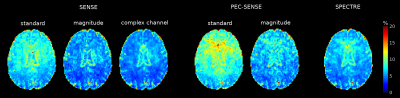
Fig. 5. The accuracy of the DKT model fit is shown in the normalised root mean squared deviation (NRMSD) between the measured data and predicted signal. Both complex channel and magnitude MP-PCA denoising methods improved the fitting, although marginal gains were apparent in reconstructions using denoised channel data. The greatest errors were observed in the noisier standard PEC-SENSE reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
4361