4360

Denoise magnitude diffusion magnetic resonance images via variance-stabilizing transformation and optimal singular-value manipulation
Xiaoping Wu1 and Kamil Ugurbil1
1Center for Magnetic Resonance Research, Radiology, Medical School, University of Minnesota, Minneapolis, MN, United States

Synopsis

We introduce a new denoising framework for denoising magnitude diffusion MRI. The framework synergistically combines the variance stabilizing transform with optimal singular-value manipulation. The usefulness of the proposed framework is demonstrated using both simulation and real-data experiments. Our results show that the proposed denoising framework can significantly improve signal-to-noise ratios across the entire brain, leading to substantially enhanced performances for estimating diffusion-tensor-related indices and for resolving crossing fibers when compared to another competing method. As such, the proposed denoising method is expected to have great utility for high-quality, high-resolution whole-brain diffusion MRI, desirable for many neuroscience and clinical applications.

Introduction

A major challenge for diffusion imaging1 is the intrinsically low signal-to-noise ratio (SNR), especially when pushing spatial resolution and/or increasing diffusion weighting2.

It has been shown that denoising3 can serve as an effective means to enhance SNR for diffusion.

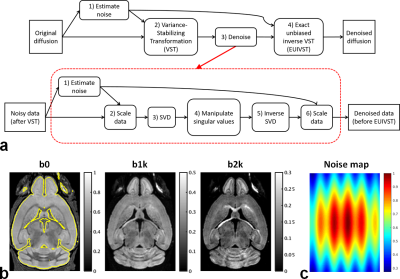
Here, we introduce a new denoising framework (Fig. 1a) that synergistically combines the variance-stabilizing transformation (VST)4 (devised for turning Rician data into Gaussian data) with a standard denoising method5 (optimized for removing Gaussian noise).

Our results for both simulation6 and real-data7 experiments show that the proposed method can significantly improve SNR, substantially enhancing performances for estimating diffusion-tensor-related indices and for resolving crossing fibers and that it outperformed another competing approach based on MPPCA8.

Methods

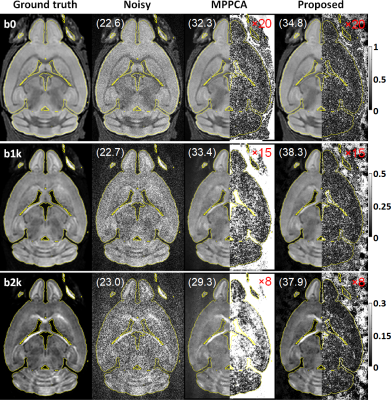
Simulation:

Noisy double-shell diffusion images were synthesized by corrupting ground-truth images (Fig. 1b) with spatially varying Gaussian noises (Fig. 1c).

Independent Gaussian noises with maximum standard deviation being 10% of maximum signal intensity of the ground-truth were added to real and imaginary channels.

Real-data experiment:

We collected brain images on a Siemens 7T MR scanner, equipped with a body gradient (70 mT/m maximum strength and 200 T/m/s maximum slew rate) and 32-channel receive capability.
A healthy subject signing a consent form approved by local IRB was scanned using the commercially available Nova RF coil.

Image acquisition was the first half of HCP 7T diffusion7, comprising two runs obtained with matched parameters.
For both runs, same double-shell q-space sampling scheme (b-values=1000 and 2000 s/mm2) was applied to obtain 71 images (including 8 b0 images), relevant imaging parameters being: 1.05-mm isotropic resolution, TR/TE=7000/71 ms, 3-fold in-plane and 2-fold slice accelerations, 132 oblique axial slices.
To allow for distortion correction in subsequent image preprocessing, two runs were acquired with Anterior-Posterior and Posterior-Anterior phase encoding directions.

Multichannel images reconstructed using split-slice GRAPPA9 were combined using the SENSE1 method9 to form final Rician images.

VST-based denoising:

At the heart of the proposed framework are sequential applications of four operation modules: 1) noise estimation; 2) VST; 3) denoising; 4) exact-unbiased inverse VST (EUIVST).

Resulting from a pilot study optimizing the implementation of the proposed framework, the finalized realization of each module was as follows.

Noise estimation opted for the VST-based method with the “VST B” function4.

Both VST and EUIVST modules employed the “VST B” function for transforming noisy diffusion data and for estimating the underlying diffusion signal.

Denoising module incorporated the standard singular-value shrinkage algorithm5. Noise estimation required by data scaling was implemented using a patch-based extension to the MPPCA method11.

Despite double-shell diffusion images, only images with b-value=1000 s/mm2 were used in the first module to estimate underlying Gaussian noise.

Following a patch-based approach for improved performance12, all modules were implemented using patches that were defined by a sliding spatial kernel of size 5x5x5.

Data analysis:

In simulation experiment, to evaluate denoising performance, we calculated peak SNR (PSNR), PSNR=10⋅log10(1/MSE), where MSE is mean squared error measuring the deviation of denoised images from the ground-truth.

In real-data experiment, human images were preprocessed by following the HCP pipelines14.
The preprocessed diffusion images were used to derive relevant diffusion metrics. Specifically, a diffusion tensor model was fit using FSL’s dtifit routine15.
Additionally, an extended ball and stick diffusion model16 tailored for estimating multiple fiber populations was fit using FSL’s bedpostx routine.

Whole-brain T1-weighted (T1w)17 and T2w18 images required by HCP preprocessing pipelines were acquired at 0.7-mm isotropic resolutions with matched FOV.

Results

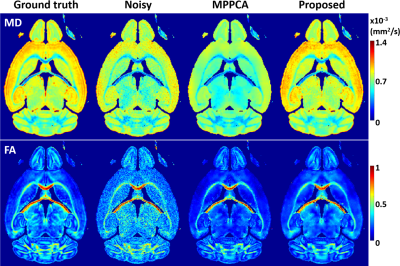
The use of the proposed method to denoise the synthesized noisy mouse data largely enhanced image quality (Fig. 2), improving overall PSNR by ~65% (37.6 vs 22.8 dB) relative to noisy data and by ~21% (37.6 vs 31.0 dB) relative to MPPCA.

The improved PSNR translated into improved estimation of both mean diffusivity (MD) and fractional anisotropy (FA) across the brain (Fig. 3), reducing the root-mean-square error for estimation of MD and FA by ~46% and ~38% relative to noisy data and by ~60% and ~19% relative to MPPCA.

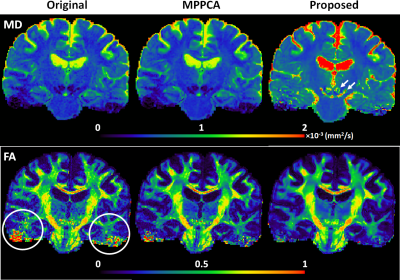
Likewise, the use of the proposed method to denoise the HCP-style diffusion largely improved image quality, leading to improved estimation of both MD and FA (Fig. 4).
The diffusion tensor fitting error reduced by ~73% and ~41% relative to noisy images and the MPPCA approach, respectively.

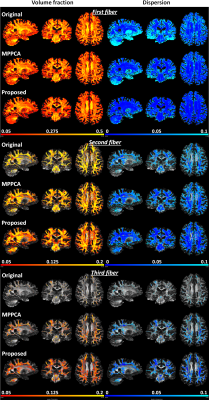
The improvement in image quality also translated into enhanced performances for estimation of fiber crossing, increasing volume fraction and decreasing dispersion for fiber orientations (Fig. 5).
Most notably, whole-brain-average dispersion reduced by ~64% for the first, by ~53% for the second, and by ~72% for the third fiber orientations relative to the noisy images and by ~44% for the first, by ~33% for the second, and by ~46% for the third fiber orientations relative to MPPCA.

Discussion and Conclusion

We have demonstrated a novel denoising method that can enhance SNR for magnitude diffusion images.
Critical to the efficacy of the new method is the synergistic combination of various techniques including noise estimation, variance stabilization, standard denoising, and patch-based implementation.
The effectiveness of the new method for noise reduction is demonstrated by using both simulation and real-data experiments.
As such, we believe that the proposed denoising method will have great utility for high-resolution whole-brain diffusion MRI, desirable for many neuroscience and clinical applications.

Acknowledgements

The authors would like to thank Steen Moeller and Mehmet Akçakaya for their stimulating discussions on denoising, Christophe Lenglet for his valuable comments on diffusion analysis, and John Strupp and Brian Hanna for their assistance in setting up computation resources. This work was supported by NIH grants including U01 EB025144, P41 EB015894, and P30 NS076408.

References

1. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 1986;161(2):401-407.

2. Uǧurbil K, Xu J, Auerbach EJ, Moeller S, Vu AT, Duarte-Carvajalino JM, Lenglet C, Wu X, Schmitter S, Van de Moortele PF, Strupp J, Sapiro G, De Martino F, Wang D, Harel N, Garwood M, Chen L, Feinberg DA, Smith SM, Miller KL, Sotiropoulos SN, Jbabdi S, Andersson JLR, Behrens TEJ, Glasser MF, Van Essen DC, Yacoub E. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. NeuroImage 2013;80:80-104.

3. Lam F, Babacan SD, Haldar JP, Weiner MW, Schuff N, Liang ZP. Denoising Diffusion-Weighted Magnitude MR Images Using Rank and Edge Constraints. Magnetic Resonance in Medicine 2014;71(3):1272-1284.

4. Foi A. Noise Estimation and Removal in Mr Imaging: The Variance-Stabilization Approach. 2011 8th Ieee International Symposium on Biomedical Imaging: From Nano to Macro 2011:1809-1814.

5. Gavish M, Donoho DL. Optimal Shrinkage of Singular Values. Ieee T Inform Theory 2017;63(4):2137-2152.

6. Zhang XY, Peng J, Xu M, Yang W, Zhang Z, Guo H, Chen WF, Feng QJ, Wu EX, Feng YQ. Denoise diffusion-weighted images using higher-order singular value decomposition. Neuroimage 2017;156:128-145.

7. Vu AT, Auerbach E, Lenglet C, Moeller S, Sotiropoulos SN, Jbabdi S, Andersson J, Yacoub E, Ugurbil K. High resolution whole brain diffusion imaging at 7T for the Human Connectome Project. NeuroImage 2015;122:318-331.

8. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016;142:394-406.

9. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magnetic Resonance in Medicine 2014;72(1):93-102.

10. Sotiropoulos SN, Moeller S, Jbabdi S, Xu J, Andersson JL, Auerbach EJ, Yacoub E, Feinberg D, Setsompop K, Wald LL, Behrens TEJ, Ugurbil K, Lenglet C. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: Reducing the noise floor using SENSE. Magnetic Resonance in Medicine 2013;70(6):1682-1689.

11. Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine 2016;76(5):1582-1593.

12. Katkovnik V, Foi A, Egiazarian K, Astola J. From Local Kernel to Nonlocal Multiple-Model Image Denoising. Int J Comput Vision 2010;86(1):1-32.

13. Gavish M, Donoho DL. The Optimal Hard Threshold for Singular Values is 4/root 3. Ieee T Inform Theory 2014;60(8):5040-5053.

14. Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 2013;80(0):105-124.

15. Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. Fsl. NeuroImage 2012;62(2):782-790.

16. Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ. Model-based analysis of multishell diffusion MR data for tractography: How to get over fitting problems. Magnetic Resonance in Medicine 2012;68(6):1846-1855.

17. Mugler JP, Brookeman JR. Three‐dimensional magnetization‐prepared rapid gradient‐echo imaging (3D MP RAGE). Magnetic Resonance in Medicine 1990;15(1):152-157.

18. Mugler JP, Bao S, Mulkern RV, Guttmann CRG, Robertson RL, Jolesz FA, Brookeman JR. Optimized Single-Slab Three-dimensional Spin-Echo MR Imaging of the Brain. Radiology 2000;216(3):891-899.

Figures

Fig. 1. a) Flowchart of the proposed denoising framework. VST aims to stabilize the standard deviation (std) of Rician data to unity so that any standard denoising (as expanded in the red box to illustrate the six steps involved) can be used. b) Synthesized magnitude diffusion images of a mouse brain serving as ground truth noise-free images for b0 (overlaid with the brain mask as indicated by the yellow curves) and representative diffusion-weighted images with b-values = 1000 and 2000 s/mm2. c) Noise map defining how the std of the Gaussian noise corrupting the data would vary in space.

Fig. 2. Example denoised images at 10% noise level obtained using the proposed method vs the MPPCA approach, alongside corresponding ground truth and noisy images for comparison. The right half of each denoised image shows a corresponding absolute difference image relative to the ground truth (amplified in magnitude for improved visualization), the numbers reported in parenthesis are b-value-dependent peak SNR in dB calculated against the ground truth for brain tissues as outlined by the brain mask (yellow). Note how the proposed denoising method outperformed the MPPCA approach.

Fig. 3. Example mean diffusivity (MD) and fractional anisotropy (FA) maps estimated from denoised images obtained at 10% noise level using the proposed method vs using the MPPCA approach, alongside the metric maps estimated from the corresponding ground truth and noisy images for comparison. Note that the use of the proposed method largely improved the estimation of MD and FA across the brain relative to using the noisy images. By contrast, the use of the MPPCA approach led to an underestimation for both MD and FA, while losing fine brain structure in multiple locations.

Fig. 4. Comparing performances for estimation of MD and FA when fitting a diffusion tensor model to the 1-mm, 7-Tesla HCP-style double-shell diffusion before (left) vs after denoising using the MPPCA approach (middle) vs the proposed method (right). Note how using the proposed method improved the performances for estimating MD and FA, especially in CSF and deep brain regions (white arrows) where MD was underestimated with original noisy images and in lower temporal lobes (white circles) where the initial signal to noise ratio was low due to RF inhomogeneity.

Fig. 5. Comparing performances for estimation of fiber crossing when fitting an extended ball and stick diffusion model to the HCP-style double-shell diffusion before vs after denoising using the MPPCA approach vs the proposed denoising method. All maps are overlaid on respective FA and thresholded at 5% volume fraction. Note how using the proposed method largely improved the estimation performances across the brain by increasing voxels of multiple fibers while reducing the dispersion of fiber orientations, relative to using the original images or the denoised images using MPPCA.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
4360