4359
Mitigating Impacts of Tissue-Heterogeneity and Noise Bias on MP-PCA Denoising for High-Quality Diffusion MRI
Cornelius Eichner1, Michael Paquette1, Angela D Friederici1, and Alfred Anwander1
1Department of Neuropsychology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
1Department of Neuropsychology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
Synopsis
Advanced diffusion MRI (dMRI) data with high resolution and strong diffusion contrast typically suffer from low SNR levels. Therefore, denoising algorithms such as MP-PCA became an essential part of current dMRI processing pipelines. To overcome challenges related to violations of MP-PCAs assumption of tissue homogeneity in typical dMRI data, we here introduce an informed-MP-PCA (iMP-PCA) algorithm taking local differences in tissue composition into account. Denoising-performance of iMP-PCA was compared to conventional MP-PCA and evaluated on both magnitude and real-valued dMRI data. iMP-PCA was shown to significantly improve denoising-performance, especially at tissue boundaries and in regions of low SNR.
Intoduction
The introduction of strong gradients to human MRI systems enabled acquisitions of diffusion MRI (dMRI) data with unprecedented diffusion contrast and resolution1,2, which however often suffer from low SNR. An adapted preprocessing pipeline including specialized denoising strategies is required to retain dMRI data quality3,4. MP-PCA denoising is currently regarded as state-of-the-art5. For each voxel, a standard kernel of N=5×5×5=125 neighboring voxels with assumed similarity is selected for all M diffusion directions. MP-PCA removes Gaussian noise by suppressing principal eigenvalues represented by a noise-specific Marchenko-Pastur distribution. However, two basic MP-PCA assumptions are not fulfilled for dMRI data: (i) similarity of proximate voxels is not given at tissue boundaries; (ii) noise in commonly used magnitude-dMRI data is non-Gaussian6. Here, we present a method to overcome these challenges by introducing a novel informed-MP-PCA-kernel (iMP-PCA) selection, which takes local tissue similarity into account; and compare its performance to conventional MP-PCA in denoising both magnitude and real-valued dMRI data.Methods
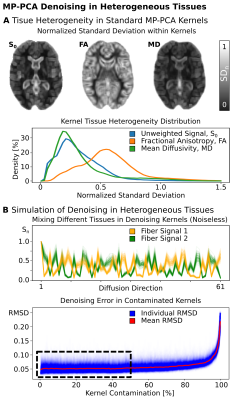
Simulations: Numerical simulations were used to investigate MP-PCA denoising-performance under (i) tissue-contamination and (ii) dMRI noise-type. (i) Synthetic dMRI signal kernels with b=1000s/mm2 and 60 diffusion directions were created for two perpendicular fiber populations with small levels of orientational dispersion. The MP-PCA-kernel was increasingly contaminated with tissue from the perpendicular kernel (both SNRb0=5). Denoising Root-Mean-Squared-Difference (RMSD) was evaluated at various contamination-levels for 1000 repetitions. (ii) Homogenous synthetic dMRI-signal (b=1000s/mm2, 60 diffusion-directions) was generated using a white-matter diffusion tensor, replicated 125 times to generate a standard MP-PCA 5×5×5 kernel, and subsequently contaminated with Rician and Gaussian noise to simulate magnitude and real-valued dMRI data. Denoising-performance was evaluated using the RMSD of denoised signals with the ground-truth for multiple SNR levels [SNRb0=1-50] for 1000 repetitions.MRI-Acquisition: 3T Connectom dMRI data of a healthy young volunteer was acquired using a 32-channel phased-array head-coil (Siemens, Germany): 1.3×1.3×1.3mm3 resolution, FoV=242×242mm2, 102sl, TR=6730ms, TE=84.6ms, PF=7/8, EPI-BW=1550Hz/px, GRAPPA=2, and SMS=2. 180 diffusion-weighted volumes were acquired at b=[1000,2000,5000]s/mm2 with 21 interspersed b=0 volumes. Reversed phase-encoding data were acquired to correct for off-resonance distortions5. DMRI phase images were reconstructed to compute unbiased real-valued dMRI data6.
Tissue-Heterogeneity-Measurements: Magnitude dMRI data were jointly corrected in one step for field-distortions, eddy-currents, and gradient non-linearities4,7; and subsequently used for a weighted DTI-fit. The normalized standard deviation (SDn) of S0(b=0), FA and MD data within a standard MP-PCA-kernel was computed voxel-wise.
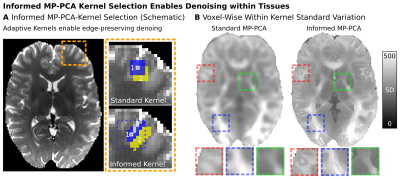
Denoising: We investigated denoising-performance using (i) iMP-PCA vs. MP-PCA on the acquired (ii) magnitude vs. real-valued dMRI data. For (i), instead of choosing the denoising-kernel as the direct neighborhood of the voxel in focus (MP-PCA), the kernel is selected adaptively, based on the voxel similarity within a larger neighborhood (9×9×9 voxels). The 125 voxels with the lowest Signal-RMSD compared to the focus-voxel are selected to create a 125×M denoising-kernel of similar tissue. This ensures using locally similar neighborhoods to reduce tissue-heterogeneity induced effects. Identical joint distortion-correction was applied for all denoised datasets4. To evaluate denoising effects, the mean and SDn of the signals were calculated voxel-wise for each b-shell.
Results
Simulations: (i) Simulations on tissue contamination show a stable MP-PCA denoising-performance for contaminations of up to 50% (Fig1). Larger kernel contamination-levels quickly increase denoising error. (ii) In homogenous tissues, denoising of real-valued data provides superior denoising accuracy, especially at low SNR levels (Fig2).Tissue-Heterogeneity Measurements: DTI-reconstructions reveal strong levels of tissue-heterogeneity within most standard MP-PCA kernels (Fig2). FA is especially heterogeneous across the brain. DTI-based kernel SD reveals only a few similar voxel-neighborhoods.
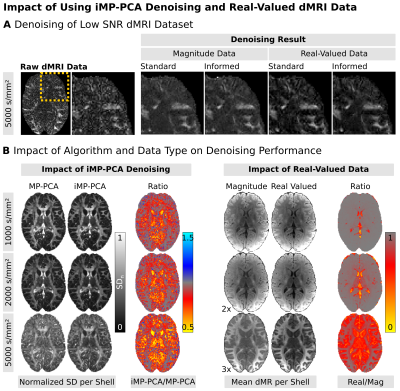
Denoising: iMP-PCA denoising is summarized in Fig3-A. Instead of using uniform kernels, iMP-PCA prevents tissue averaging by adaptively varying kernel-shapes based on the similarity of the voxel-wise dMRI signal of the different measurements. This allows signals of similar tissue types to be grouped for better noise reduction. The tissue boundary preservation of iMP-PCA is displayed in Fig3-B. Denoising of a low-SNR dMRI dataset is visualized in Fig4-A. Visual inspection shows the highest denoising-performance for iMP-PCA on real-valued data (i.e., no signal bias and reduced noise-level). Fig4-B separately visualizes the impact of (i) the denoising algorithms and (ii) dMRI data type. Fig4-B-Left visualizes the effect of iMP-PCA denoising for different diffusion-weightings. iMP-PCA retains tissue-related signal differences (i.e. in highly anisotropic white matter regions) and reduces the overall noise-level, especially close to tissue boundaries. Fig4-B-Right shows that denoising real-valued dMRI data reduces the signal bias and achieves stronger diffusion signal-attenuation, particularly at low SNR levels.
Discussion
We evaluated the impact of kernel selection and dMRI data-type for advanced dMRI denoising. Using simulations and acquired data, we showed that tissue-heterogeneity within conventional MP-PCA-kernels reduces denoising accuracy. We overcame this challenge by introducing an informed-MP-PCA-kernel (iMP-PCA) selection algorithm, which takes local tissue similarity into account. We showed that iMP-PCA achieves superior denoising-performance compared to conventional MP-PCA approaches, reducing overall image noise while retaining local signal variations from tissue anisotropy. We further showed that combined iMP-PCA with real-valued dMRI data significantly improves denoising-performance on advanced dMRI data - especially at high resolutions and with strong diffusion-weightings.Acknowledgements
CE and MP are supported by the SPP2041 program "Computational Connectomics" of the German Research Foundation (DFG). MP is supported by a NSERC scholarship (PDF-502732-2017) from Canada.References
1. Setsompop K et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 80:220-33, 2013
2. Jones D et al. Microstructural imaging of the human brain with a 'super-scanner': 10 key advantages of ultra-strong gradients for diffusion MRI. Neuroimage. 182:8-38, 2018
3. Glasser MF et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 80:105-24, 2013
4. Eichner C et al., A joint recommendation for optimized preprocessing of connectom diffusion MRI data. In ISMRM 27:1047, 2019
5. Veraart J et al. Denoising of diffusion MRI using random matrix theory. Magn Reson Med. 76:1582-93, 2016
6. Eichner C et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage. 22:373-84, 2015
7. Andersson JL and Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage. 125:1063-78, 2016
Figures
Figure 1: A Computations of S0, FA, and MD normalized standard deviation (SDn) reveal strong tissue-heterogeneity within standard MP-PCA kernels. B Denoising-error on Fiber-1 signals contaminated with Fiber-2 signals strongly increases for contamination levels > 50%. Note that real tissue-heterogeneity will typically be stronger compared to this ideal example of two crossing fibers (additional heterogeneity sources include S0, MD, FA). Hence, denoising accuracy will likely be reduced for real-world dMRI data.
Figure 2: A Noisy voxels within homogeneous kernel data (blue) displayed alongside the ground-truth dMRI signal (green) and the denoised signal (orange). iMP-PCA achieves significantly better denoising accuracy for real-valued dMRI data with Gaussian noise, based on RMSD B The denoising error (RMSD) on real-valued dMRI data remains small, even for low SNRs. Magnitude dMRI data RMSD strongly increases below SNR=10.
Figure 3: A The iMP-PCA kernel is defined by similarity of voxels within a larger region (dotted blue). Best matching voxels are selected for denoising. Every voxel potentially has its own kernel shape, depending on the underlying tissue. B The voxel-wise intra-kernel standard variation (SD) shows tissue-preserving characteristics of iMP-PCA. Informed adaptive kernels result in separation of tissue types in cortex and specific white matter tracts (see enlargements).
Figure 4: A iMP-PCA denoising with real-valued dMRI data is superior with improved signal-attenuation and reduced noise B Left: iMP-PCA denoising retains tissue-related, large signal-variations in highly anisotropic white matter regions - however, it reduces noise in less anisotropic regions, such as in gray matter for all b-shells (ratio). Right: Real-valued dMRI denoising impact becomes evident at b=2000 with a stronger noise attenuation in central grey matter regions (ratio).