Introduction

Diffusion weighted imaging (DWI) and apparent-diffusion-coefficient (ADC) mapping are important diagnostic imaging tools for various diseases including stroke¹ and cancer^{2, 3}. Compared with DWI, ADC mapping is quantitative but requires a longer scan time. Parallel imaging^{4, 5} is a common in-plane acceleration method, but the acceleration rate is often limited by g-factor. Compressed sensing⁶ is technically challenging for diffusion imaging, potentially due to the difficulty of incorporating random k-space sampling into EPI, and incurrence of eddy currents. SUPER (Shift Undersampling improves Parametric mapping Efficiency and Resolution) is a novel acceleration method for parametric mapping⁷. In particular, SUPER is based on uniform k-space undersampling and thus more robust against eddy currents. Here we propose a modified SUPER method to accelerate ADC mapping in the presence of nonlinear phase evolution, and demonstrate its performance in 6 healthy subjects.

Methods

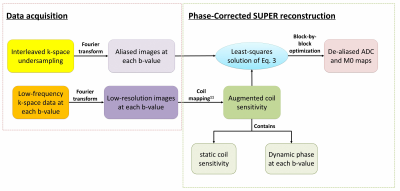
A detailed description of SUPER can be found in Ref 7. In brief, SUPER treats each contrast-weighted image in a parametric mapping task as a separate “coil”, and leverages the methodology of parallel imaging to accelerate parametric mapping. At each b-value, the signal acquired with SUPER is aliased from spatially modulated signals at voxels uniformly spaced along the phase-encoding direction. The aliasing is similar to that of Cartesian SENSE⁴, but with nonlinear “coil sensitivity” and spatial modulation yielded by interleaved undersampling:$$\textrm{Eq 1}:{y_{ml}} = \sum\limits_{r = 0}^{R - 1} {{w_{rl}}s_{mr}^0\left( {M{0_r}\exp ( - {b_l} \cdot AD{C_r} + i{\psi _{rl}})} \right)}$$where $$${R}$$$ is the reduction rate, $$${w_{rl}} = \frac{1}{R}\exp (\frac{{2\pi irl}}{R})$$$ the modulation⁷ of the $$${r}$$$th voxel, $$$s_{mr}^0$$$ the sensitivity of the $$$m$$$th coil at the $$$r$$$th voxel, and $$${\psi _{rl}}$$$ the phase at the $$$r$$$th voxel, which changes nonlinearly for each b-value due to eddy currents⁸ and bulk motion^{9, 10}.The goal is to estimate M0 and ADC from the aliased data $$${y_{ml}}$$$.

Phase correction is needed for accurate estimation of ADC/M0 using $$$\textrm{Eq 1}$$$. In this work, we developed a phase-correction method for SUPER based on the coil-mapping strategy developed by McKenzie et al¹¹(Figure 1). Specifically, $$$\exp (i{\psi _l})$$$ in $$$\textrm{Eq 1}$$$ was measured by acquiring 24 central k-space lines for each b-value, and dividing the corresponding low-resolution image acquired from each coil by the sum-of-squares image from all coils¹¹.This was a valid approach given the assumption that phase mainly resides in the central part of k-space. This method generates an augmented coil map $$${s_{ml}}$$$, which is composed of static coil map $$$s_m^0$$$ and the dynamic phase:$$\textrm{Eq 2}:{s_{ml}} = s_m^0 \cdot \exp (i{\psi _l})$$Substituting $$$\textrm{Eq 2}$$$ into $$$\textrm{Eq 1}$$$ leads to$$\textrm{Eq 3}:{y_{ml}} = \sum\limits_{r = 0}^{R - 1} {{w_{rl}}{s_{mlr}} \cdot (M{0_r}\exp ( - {b_l} \cdot AD{C_r}))}$$which can be easily solved with a least-squares criterion.

Imaging: Six healthy subjects (age 26±4, 3 male) were scanned in a 3T scanner (uMR790, Shanghai United Imaging Healthcare, Shanghai, China) after providing written informed consent, with a diffusion-weighted spin-echo EPI sequence using a 24-channel (17 used in acquisition) head coil. Eight axial slices were imaged in the upper-to-mid brain with FOV of 240×240mm²,image size 80×80, and slice-thickness 5mm.Five b-values were used: b=0, 200, 400, 600, and 800sec/mm². Other parameters were: TR/TE/bandwidth/NEX/interpolation/flip-angle = 4000ms/86ms/1790Hz/pixel/1/2/90°. k-Space data was retrospectively undersampled for ADC mapping based on non-acceleration, SENSE (R=2), SUPER (R=2), and SUPER-SENSE (combined SUPER and parallel imaging, R=4). Data along 3 diffusion-encoding directions was averaged to form the final ADC/M0 maps. Non-accelerated reconstruction was considered the gold standard for image quality assurance.

Results

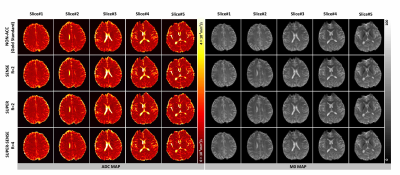
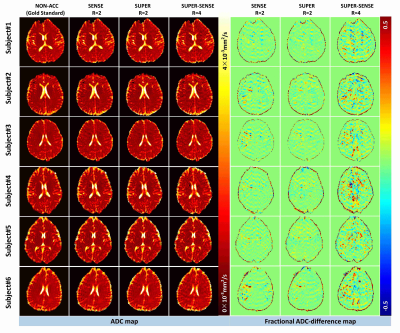
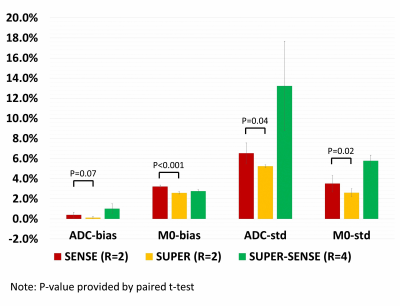
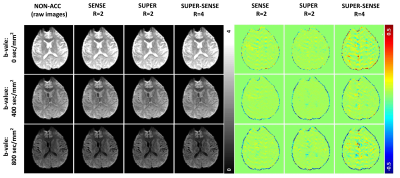
Figure 2 ows representative ADC and M0 maps in 5 slices of 1 healthy subject. All 3 acceleration methods achieved similar image quality compared with non-accelerated method. Figure 3 shows the ADC maps from the central slice in all 6 subjects, and the fractional ADC-difference maps for 3 acceleration methods, calculated by (ADC_acc–ADC_nonacc)/ADC_nonacc. SUPER showed less aliasing artifacts compared to SENSE, potentially due to inaccurate coil mapping caused by imperfect EPI ghost correction¹². SUPER-SENSE showed mild noise and aliasing artifacts with a reasonable image quality.Notably, even very small features in the brain were well preserved in the SUPER-SENSE maps.

Figure 4 shows comparison of bias and standard deviation between the acceleration methods. There was small bias in ADC and slightly larger bias in M0 for all methods. SUPER led to better accuracy and precision than SENSE under all criteria, and this is remarkable considering that SUPER only had 5 effective “coils” while SENSE had 17. Figure 5 shows retrospectively synthesized DWI images from the 3 acceleration methods, which were all similar to the raw images. The average computational time per voxel for non-acceleration, SENSE, SUPER, and SUPER-SENSE was 3.0ms, 3.8ms, 2.8ms, and 3.0ms, respectively, which are similar between all methods.

Conclusions

We demonstrated a novel development and application of SUPER for accelerating ADC mapping. SUPER with phase correction achieved better image quality compared to SENSE even with less “coils”, suggesting a better conditioning of the underlying inverse problem. SUPER-SENSE at 4-fold acceleration demonstrated reasonable image quality and noise amplification. The reduced echo-train with SUPER and SUPER-SENSE may improve SNR and EPI distortion, and may also be traded-off for higher image resolution. Although further investigation involving prospective undersampling is needed, the preliminary data suggests that SUPER is a practical and accurate approach for accelerating ADC mapping.

Acknowledgements

The authors would like to thank Zhaopeng Li at Shanghai United Imaging Healthcare for helpful discussions on DWI data preprocessing.