Introduction

Diffusion-weighted imaging (DWI) plays a crucial role in clinical neurology and neuroscience studies¹. Due to its fast acquisition speed, single-shot EPI is widely used in DWI. However, with limited bandwidth along the phase encoding direction, single-shot EPI suffers from distortion and blurring. Recently, efforts have been made to use multi-shot methods to address these problems^2-4. Among them, a new point-spread-function (PSF) encoded EPI using Tilted-CAIPI acquisition and reconstruction has been proposed to provide distortion- and blurring-free images with acceleration factors over 20 fold^5-6. Nevertheless, when field inhomogeneity is severe, it can be difficult to recover the undersampled data correctly and more shots are needed to improve reliability, which increases scan time. In this work, based on the similar low frequency content among images obtained at different k_y locations in PSF-EPI, we developed a low-rank based method using the signal correlation along the k_y-encoding dimension to improve the accuracy of reconstruction.

Theory

PSF-EPI
In PSF-EPI, an additional phase-encoding called PSF-encoding is added before the original EPI readout. Since different PSF-encoding signals obtained at the same k_y are acquired at the same echo times, PSF direction is a distortion-free dimension. Thus, 2D distortion- and blurring-free images acquired at different echo times can be obtained.

Low rank property for PSF-EPI
In PSF-EPI acquisition, a 2D(x-psf) image obtained at k_y =m can be described as follows,
$$I_m=I_0 e^{-m∆t/T_2^* } e^{-ik_m y}e^{-iγ∆Bm∆t}$$
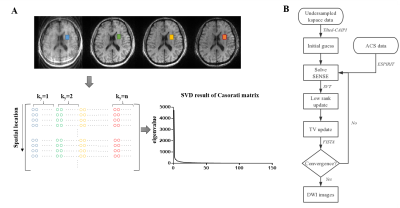
Since these images share the same low frequency magnitude component $$$I_0$$$, correlation exists between these 2D images and a low rank matrix can be formed. As shown in Figure. 1A, we construct the low rank matrix by stacking points at the same location from different x-psf images together. The different colors represent images at different k_y locations. The SVD result proves its low rank property.

Reconstruction model
Considering that optimization for low rank constraint is a non-convex problem, the nucleus norm penalty is used. By minimizing the nucleus norm, the rank of the matrix will be reduced. This optimization is achieved by single value thresholding (SVT) algorithm.
Due to the high acceleration number used in PSF-EPI, the images are noisy and the SNRs of the images suffer. To further improve image reliability, total variation model is introduced along with nucleus norm penalty to further improve the SNR while preserving information from fine brain structures.
Since PSF-EPI is a multi-shot technique, the shot-to-shot phase variation induced by physiological motion should be corrected in reconstruction. Thus, a navigator is added to each shot to estimate the phase of individual shot respectively⁷.The combined reconstruction model is shown as follows,
$$\min_m⁡‖DFSPm_i-y‖_2^2+μ|M|_*+αTV(m)$$
Where, D, F, P and S represent sampling pattern, Fourier transform, phase compensation and sensitivity map, respectively; $$$m_i$$$ represents image magnitude at k_y=i; y represents sampled k-space signal; M represents the formed low-rank matrix.
The first term in the cost function enforces data consistency. The second term serves as low rank constraint and the last term introduces total variation.
In this work, the optimization problem is solved iteratively. Figure. 1B shows the pipeline of the reconstruction.

Methods

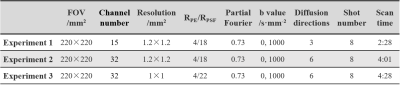
Data acquisition
With institutional review board approval, data were obtained from 3 healthy volunteers on a 3T Philips Achieva scanner (Philips Healthcare, Best, The Netherlands) using the PSF-EPI sequence. Three experiments were carried out to test the performance of the proposed method. The first experiment used a 15-channel head coil to validate the proposed method. The second and the third experiments used a 32-channel head coil to test the method with different resolution data and DTI quantification. The scan parameters are shown in Table 1.

Image reconstruction
Images were reconstructed using the Tilted-CAIPI method and the proposed method, respectively. Sensitivity maps were calculated from b0 data using ESPIRIT⁸ and colored FA maps were calculated using FSL⁹.

Results and discussion

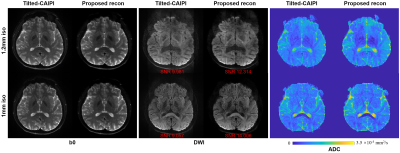
Figure 2 shows 3 slices of the DWI images from experiment 1. Compared to using Tilted-CAIPI, the noise levels of reconstructed images using the proposed method decrease and the SNRs improve since the low rank constraint jointly updates all 2D images along the k_y dimension.
Similar improvements can be found when the image resolution increases. Figure 3 shows the reconstructed images from experiments 2 and 3. The 1 mm isotropic resolution DWI image reconstructed from Tilted-CAIPI (middle panel) is noisier than that from the proposed recon. The SNR values also indicate the improvement for both resolution DWI images when using the proposed reconstruction method. ADC values of the brain tissues lie within the normal range of healthy adults.
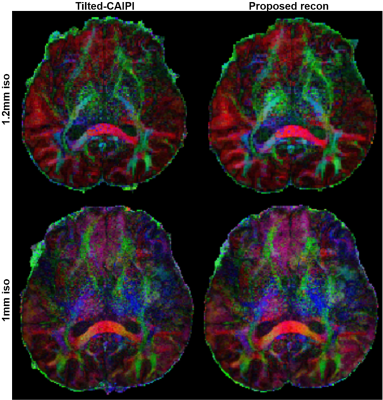
We further examine the proposed method in DTI. The colored FA maps are shown in Figure 4. Compared to using Tilted-CAIPI, the obtained cFA maps using the proposed method are visually better, as the noise levels decrease. Additionally, the small structures can also be preserved.

Conclusion

The proposed low-rank based reconstruction algorithm can improve the DW PSF-EPI images obtained from Tilted-CAIPI with increased SNR. It may have potentials to improve the reliability of Tilted-CAIPI accelerated PSF-EPI.

Acknowledgements

No acknowledgement found.