4348
Rapid, structure-preserving denoising of DTI data via tight framelet thresholding.1Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 2Radiology, University of Cincinnati College of Medicine, Cincinnati, OH, United States
Synopsis
In this work it is demonstrated that computationally efficient deniosing can be done using thresholding of wavelet coefficients without sacrificing image quality relative to state-of-the-art patch-based methods. This is achieved by combining use of a redundant, directional tight wavelet frame with the Karhunen-Loeve transform along the "directions" dimension. An efficient GPU implementation of the algorithm required less than 30 seconds to process even relatively large DTI datasets (e.g. 96x96x60x203). The proposed approach should find use in SNR-challenged acquisitions such high resolution DTI, DKI and DSI.
Introduction
Diffusion weighted imaging (DWI) variants such as diffusion kurtosis imaging (DKI1) and diffusion spectrum imaging (DSI2) result in the acquisition of many images at a range of diffusion directions and weightings (b-values). At higher b-values, the signal-to-noise ratio (SNR) of diffusion scans is limited, particularly at higher spatial resolutions (<= 2 mm). This has motivated a number of methods for denoising diffusion data in the literature3-6. Among these, methods based on a local principal component analysis (PCA) provide high performance, but are computationally intensive4,5. In this work, we propose a computationally simpler thresholding approach that remains competitive with local-PCA approaches. This makes it well suited for use on the increasingly large datasets encountered in practice.The use of wavelet thresholding for denoising was pioneered by Donoho and colleagues7. The success of the approach relies on the fact that the representation of natural images (or volumes) tends to be sparse in the wavelet domain (i.e. the energy is concentrated into a small fraction of the coefficients), while the noise is not. A denoised signal can be obtained by appropriately thresholding the coefficients.
Methods
A wavelet thresholding approach was applied to two different 4D datasets, each indexed by (x, y, z, d) where (x, y, z) are spatial indices and d enumerates the various diffusion weightings applied.Simple wavelet thresholding is not competitive with state of the art DTI denoising approaches such as local PCA (see Fig. 3a). In this work, we modify the thresholding-based approach in three ways: 1.) Sparsity is improved by applying the (orthogonal) Karhunen-Loeve transform (KLT) along the “diffusion direction” axis. This transform compacts most of the energy into a fairly small number of principal diffusion components. 2.) The orthogonal discrete wavelet transform is replaced by a redundant transform with better directional selectivity. We chose tensor-product complex tight framelets (TP-CTF8) in this work for its computational efficiency and relatively low redundancy (<8 in 3D). 3.) We apply block thresholding of the coefficients via the NeighShrinkSURE9 approach. Fig.1 shows a block diagram of the proposed approach.
The software PyWavelets10 was extended to support the tensor-product complex tight framelet transform. We evaluated the denoising on two multishell DTI datasets bundled with the Dipy software package11. The first (CFIN Multishell12) consists of 203 diffusion weightings at b-values up to 3000 s/mm2 collected at 2.5 mm isotropic resolution. The second (NTU Multishell13) is 1.9 mm isotropic with 33 directions repeated for 15 separate b-values ranging from [0, 4000 s/mm2]. The first dataset has a higher SNR, but a spatially variable noise distribution; while the second dataset better illustrates a low SNR scenario.
Results
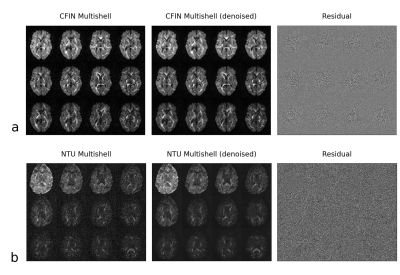
Representative slices at a subset of diffusion weightings/directions are shown for the proposed approach in Fig. 2. It can be seen that in both cases the noise is effectively removed without substantial blurring of fine details (observed as a lack of edge information in the residuals).Fig. 3 compares results for various methods for wavelet denoising of the NTU dataset. Denoising was performed on the 4D data as a whole, but only a single slice at one b=4000 direction is shown for visualization. Both cases involving the TP-CTF framelet transform and KLT preserve underlying structure well. The case marked "+ Neigh" used the NeighShrinkSURE block thresholding. The rest of the wavelet approaches used a locally adaptive14 version of the BayesShrink15 soft thresholding. The GFA maps are very similar for all "KLT+wavelet" and the local-PCA approach. This is likely because the presence of 203 total acquisitions (at a range of b-values) has resulted in reasonable composite SNR even when individual volumes may appear somewhat degraded.
Computation time for the local PCA method as implemented for multi-core CPU computation for CFIN Multishell data with shape (96, 96, 19, 496) was 5006 seconds. In contrast a largely single-core CPU implementation of the proposed method took 608 seconds while a GPU-based implementation took only 27 seconds (on an NVIDIA 1080TI GPU) .
Discussion
The proposed approach is tuned for Gaussian noise, while the underlying data used in the experiments were magnitude images formed after coil combination. There is some intensity bias that is visible as non-zero signal in background regions (Fig 2b). For high SNR regions, Gaussian noise is a good approximation, but in low signal regions there will be a bias that depends on both acquisition and reconstruction parameters16.Rather than adapt the noise model to account for non-Gaussian noise, it may be preferable to operate directly on the complex data as produced by SENSE-based reconstruction. Such an approach has been demonstrated for a non-local PCA-based denoising algorithm6. The approach proposed in this work can operate equally well on complex-valued data. This would solve the problem of bias seen for the lower SNR data in Fig. 2b.Conclusion
The proposed approach produces images that appear of equal quality to an existing local PCA approach, while requiring 1-2 orders of magnitude less computation time.The general approach illustrated in Fig 1, is not restricted to diffusion MRI, but can potentially be applied to a wide variety of other quantitative parameter mapping experiments as well.
Acknowledgements
No acknowledgement found.References
1. Jensen JH, Helpern JA, Ramani A, et. al. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 2005; 53(6):1432–1440.
2. Wedeen VJ, Wang RP, Schmahmann JD, et al. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. NeuroImage. 2008;41(4):1267–1277.
3. Aja-Fernández S, Niethammer M, Kubicki M et. al. Restoration of DWI Data Using a Rician LMMSE Estimator. IEEE Trans. Med. Imaging 2008;27(10):1389-1403.
4. Manjón JV, Coupé P, Concha L et. al. Diffusion Weighted Image Denoising Using Overcomplete Local PCA. PloS One 2013;8(9):e73021.
5. Veraart J, Novikov DS, Christiaens D, et. al. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:394-406.
6. Chen NK, Chang HC, Bilgin A, et. al. A diffusion-matched principal component analysis (DM-PCA) based two-channel denoising procedure for high-resolution diffusion-weighted MRI. PloS One 2018;13(4):e0195952.
7. Donoho DL and Johnstone IM. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994:81(3): 425-455.
8. Han B, Mo Q, Zhao Z. Compactly Supported Tensor Product Complex Tight Framelets with Directionality. SIAM J. Math. Anal. 2015;47(3):2464-2494.
9. Zhou D and Cheng W. Image denoising with an optimal threshold and neighbouring window. Pattern Recognition Letters 2008;29(11):1694–1697.
10. Lee GR, Gommers R, Waselewski F, et. al. PyWavelets: A Python package for wavelet analysis. Journal of Open Source Software 2019;4(36):1237;https://doi.org/10.21105/joss.01237.
11. Eleftherios G, Matthew B, Bagrat A, et. al. Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics 2014;https://doi.org/10.3389/fninf.2014.00008.
12. Hansen B. and Jespersen S. Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Sci Data 2016;3:no. 160072.
13. Data from Advanced Biomedical MRI Lab, National Taiwan University Hospital. http://brain.labsolver.org/diffusion-mri-data/ntu-dmri-data
14. Sendur L and Selesnick IW. Bivariate shrinkage with local variance estimation. IEEE Signal Processing Letters 2002;9(12):438-441.
15. Chang SG, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Processing 2000;9(9):1532-1546.
16. Aja-Fernández S. and Vegas-Sánchez-Ferrero G. Noise Estimation in Multiple-Coil MR Data. In: Statistical Analysis of Noise in MRI. 2016, Springer, Cham.
Figures