Introduction

Multi-shot diffusion weighted imaging (DWI) holds a great potential for high resolution diffusion imaging as, compared to single-shot imaging, it is less sensitive to magnetic field inhomogeneities and induces less off-resonance distortions[1]. Unfortunately, multi-shot DWI often suffers from ghosting artifacts resulting from shot-to-shot phase differences caused by non-diffusive bulk motion[2,3].
To reduce phase related artifacts, several strategies have been proposed. A common approach is to estimate the phase map in a pre-processing step from a fast, low resolution navigator scan[4] or the fully sampled central part of the k-space[5,6] and then incorporate it in the reconstruction step. Alternatively, the phase map can be estimated retrospectively from the data by exploiting different properties of the data such as the Structured Low-Rank Property of multi-shot DW Data[7] or smoothness of phase variation[8]. However, phase correction in multi-shot diffusion MRI still remains challenging, both in terms of the acquisition of a well-matched navigator image as well as in terms of robust estimation and correction of phase errors.
In this work, we propose a framework that enables estimation of phase maps jointly with diffusion tensor parameters directly from q-k-space. Our framework avoids the conventional two-step-approach (reconstruction followed by parameter estimation) and follows a more direct parameter estimation approach in which the joint information of all the acquired points of different shots in q-k-space is exploited. As a proof of concept, we model the phase as a constant value for each shot with random changes from shot to shot.

Method

Adopting the conventional diffusion tensor imaging (DTI) model, the n-th noise free 2D diffusion weighted image $$$\boldsymbol{f}_{n}(\boldsymbol{r})$$$, with $$$\boldsymbol{r}$$$ representing the spatial coordinate vector, can be modeled as:$$\boldsymbol{f}_{n}(\boldsymbol{r})=\boldsymbol{S}_{0}(\boldsymbol{r})e^{\boldsymbol{B}_{n}\overline{\boldsymbol{D}}(\boldsymbol{r})}e^{i\boldsymbol{\theta}_{n}(\boldsymbol{r})},(Eq.1)$$where $$$n\in\{1,\ldots,N\}$$$ denotes the diffusion weighting index, $$$\boldsymbol{S}_{0}$$$ the magnitude of the non-diffusion weighted image, $$$\overline{\boldsymbol{D}}=\left\{\boldsymbol{D}_{xx},\boldsymbol{D}_{xy},\boldsymbol{D}_{xz},\boldsymbol{D}_{yy},\boldsymbol{D}_{yz},\boldsymbol{D}_{zz}\right\}^{T}$$$ the vector of diffusion tensor elements, $$$\boldsymbol{\theta}_{n}$$$ the image phase and $$$\boldsymbol{B}_{n}=\left\{-b_{n}g_{x n}^{2},-2b_{n}g_{xn}g_{yn},-2b_{n}g_{xn}g_{zn},-b_{n}g_{yn}^{2},-2b_{n}g_{yn}g_{zn},-b_{n}g_{zn}^{2}\right\}$$$ contains the information of diffusion weighted data acquisition, with $$$b_{n}$$$ the diffusion weighting factor and $$$g_{xn},g_{yn}$$$ and $$$g_{zn}$$$ the elements of the n-th normalized diffusion sensitizing gradient vector $$$\boldsymbol{g}_{n}=\left(g_{xn},g_{yn},g_{zn}\right)^\boldsymbol{T}$$$. In this work, the image phase is assumed to be constant across each shot, i.e., $$$\boldsymbol{\theta}_{n}(\boldsymbol{r})=\theta_{n}$$$, while randomly varying shot to shot.
In our proposed Direct Diffusion and Phase parameter Estimation (DDPE-MS) framework, diffusion tensor and phase parameters are estimated directly from multi-shot k-q space data that can be modeled as:$$\boldsymbol{d}_{n}(\boldsymbol{k})=A_{n}(\boldsymbol{k}) \mathcal{F}\left(\boldsymbol{f}_{n}(\boldsymbol{r})\right)+\boldsymbol{e}(\boldsymbol{k}),(Eq.2)$$with $$$\boldsymbol{d}_{n}(\boldsymbol{k})$$$ the measured data of the n-th diffusion weighted image at k-space point k, $$$\mathcal{F}$$$ the 2D Fourier transform operator, $$$\boldsymbol{A}_{n}(\boldsymbol{k})\in\{0,1\}$$$ a binary matrix that describes the sampling pattern of each shot and $$$\boldsymbol{e}(\boldsymbol{k})$$$ a 2D complex valued matrix containing zero mean Gaussian noise. The least squares estimator of the diffusion tensor $$$\overline{\boldsymbol{D}}(\boldsymbol{r})$$$ (in all voxels) and vector of phase parameters $$$\boldsymbol{\theta}=\left(\theta_{1},\ldots,\theta_{N}\right)^{T}$$$ (i.e., one parameter for each shot) is then given by: $$\widetilde{\boldsymbol{D}}(\boldsymbol{r}),\widetilde{\boldsymbol{\theta}}=\arg \min _{\overline{\boldsymbol{D}},\boldsymbol{\theta}}\left(\Sigma_{n}||\boldsymbol{d}_{n}(\boldsymbol{k})-\boldsymbol{A}_{n}(\boldsymbol{k})\mathcal{F}\left(\boldsymbol{f}_{n}(\boldsymbol{r})\right)\|_{2}^{2}\right),(Eq.3)$$

Experiments

To quantify the performance of the proposed DDPE-MS estimator (Eq.3), multi-shot k-q-space data was generated using the models described by Eqs.1 and 2, assuming 6 b0 images, three shells of b-values equal to 0.25, 1.15 and 2$$$ms/\mu m^{2}$$$ and N=186 diffusion directions (uniformly distributed on the unit sphere). For each diffusion weighting, the k-space was sampled in two shots, covering the odd and even lines of the k-space, respectively. The images corresponding with each shot were generated with a constant image phase map, where the phase varied randomly from shot to shot to mimic phase jumps that are typically encountered in multi-shot imaging. All k-q-space data were then corrupted by additive complex valued zero mean Gaussian white noise. For statistical analysis, 20 datasets with different noise realizations were generated, and this for 4 values of the SNR, where the SNR was defined as the ratio of the average signal of the magnitude b0 image to the background noise standard deviation. The diffusion and phase parameters were then estimated from multi-shot k-q-space data using Eq.3. To evaluate the accuracy and precision with which the proposed DDPE-MS method can estimate the diffusion tensor parameters from the multi-shot data in the presence of the phase jumps, estimates of the bias and standard deviation are computed for the Mean Diffusivity (MD) metric. These values are then compared with estimated bias and standard deviation values obtained following a more conventional approach in which image reconstruction (applying an inverse FT to the two-shot k-space data) is followed by voxel-wise fitting the DTI model to the reconstructed magnitude images (ISDE-MS).

Results and discussion

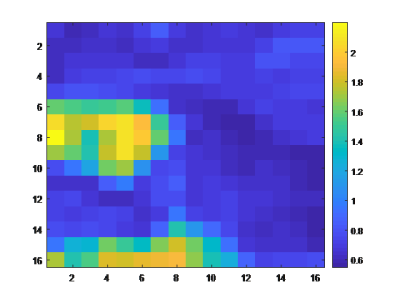
The results show that the newly proposed method provides more accurate and precise estimates of MD than the voxel-wise two-step approach that ignores phase differences.
Fig.1 shows the ground truth MD map.
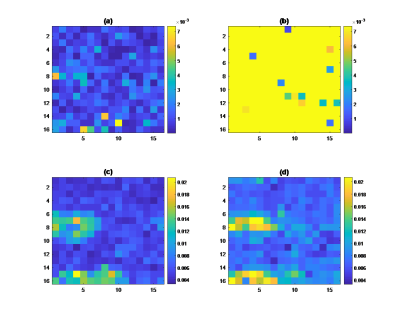
Fig.2 shows maps of the estimated absolute value of the bias and standard deviation of the MD estimates for both the DDPE-MS and ISDE-MS methods.
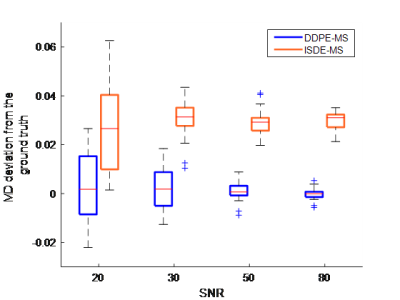
Fig.3 shows box plots of the deviations of the MD estimates from the ground truth value for one arbitrarily selected voxel for different values of the SNR.

Conclusion

In this work, we presented a proof-of-concept for simultaneous estimation of diffusion and phase map parameters directly from multi-shot k-q-space diffusion data. Future work will include an extension to under-sampling and multi-channel acquisition, as well as the incorporation of more accurate phase models[9].

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 764513.