4345
Phase-Constrained Reconstruction of High-Resolution Multi-shot Diffusion Weighted Image1Department of Electronic Science, Xiamen University, Xiamen, China, 2School of Medicine, Tsinghua University, Beijing, China, 3School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
Synopsis
Multi-shot DWI improves the image resolution, while it induces phase variation at the same time. We introduce a smooth phase constraint of each shot image into multi-shot DWI reconstruction procedures by imposing the low-rankness of Hankel matrix constructed from the k-space data. The image is further improved with a partial sum of singular values in low-rank matrix reconstruction. Results on brain imaging data show that the proposed method outperforms the state-of-the-art methods in terms of artifacts removal and is compatible to partial Fourier sampling in accelerated DWI.
Purpose
Single-shot echo-planar imaging (EPI) acquisition is currently conventional method used for DWI acquisition due to its motion immunity and short acquisition time. However, single-shot DWI usually has low bandwidth along the phase encoding direction, which makes this imaging method sensitive to field inhomogeneity and eddy currents. While multi-shot DWI improves image resolution, it brings phase variations among different shots at the same time. Recently, the low-rank Hankel matrix (LRHM) completion methods have been exploited to reconstruct MRI image1-5 and spectrum6-10. In this work, we introduce a smooth phase constraint of each shot image into multi-shot DWI reconstruction by imposing the low-rankness of Hankel matrix constructed from the k-space data. The image is further improved with a partial sum of singular values in low-rank matrix reconstruction. Results on brain imaging data show that the proposed method outperforms the state-of-the-art methods in terms of artifacts removal and is compatible to partial Fourier sampling in accelerated DWI.Methods
The proposed Phase-constrained Low-Rank Hankel Matrix (PLRHM) multi-shot DWI reconstruction method can be formulate as: \[\underset{\mathbf{X}}{\mathop{\min }}\,\frac{\lambda }{2}\sum\limits_{i=1}^{I}{||{{\mathbf{Y}}_{i}}-\mathsf{\mathcal{U}\mathcal{F}}{{\mathbf{C}}_{i}}{{\mathsf{\mathcal{F}}}^{-1}}\mathbf{X}||_{F}^{2}}+||{{\widetilde{\mathsf{\mathcal{P}}}}_{s}}\mathbf{X}|{{|}_{*}},\] where $$$\mathbf{X}=[{{\mathbf{x}}_{1}},..,{{\mathbf{x}}_{N}}]$$$ denotes concatenated matrices of k-space data of shots, $$${{\widetilde{\mathsf{\mathcal{P}}}}_{s}}\mathbf{X}=[{{\mathsf{\mathcal{P}}}_{s}}{{\mathbf{x}}_{1}},...,{{\mathsf{\mathcal{P}}}_{s}}{{\mathbf{x}}_{k}},...,{{\mathsf{\mathcal{P}}}_{s}}{{\mathbf{x}}_{N}}]$$$, $$${{\mathsf{\mathcal{P}}}_{s}}$$$ is an operator that converts $$${{\mathbf{x}}_{k}}$$$ into a Hankel matrix, $$$\mathsf{\mathcal{F}}$$$ the Fourier transform operator, $$${{\mathsf{\mathcal{F}}}^{-1}}$$$ the inverse Fourier transform operator, $$${{\mathbf{C}}_{i}}$$$ the i-th channel coil sensitivity map, $$$\mathsf{\mathcal{U}}$$$ an operator that under-samples k-space data and zero-fills the non-sampled data points, $$${{\mathbf{Y}}_{i}}$$$ the i-th channel sampled k-space data, $$$\lambda $$$ a regularization parameter that balances the data consistency and low-rankness constraint, $$$||\cdot |{{|}_{F}}$$$ represents Frobenius norm which constrains the data consistency, $$$||\cdot |{{|}_{*}}$$$ denotes the nuclear norm of a give matrix.Besides, in the low rank matrix reconstruction, it has been found that the minimization of nuclear norm may lead to sub-optimal performance, and some researches try to minimize the partial sum of singular values11,12. Therefore, our proposed model is further revised as: \[\underset{\mathbf{X}}{\mathop{\min }}\,\frac{\lambda }{2}\sum\limits_{i=1}^{I}{||{{\mathbf{Y}}_{i}}-\mathsf{\mathcal{U}\mathcal{F}}{{\mathbf{C}}_{i}}{{\mathsf{\mathcal{F}}}^{-1}}\mathbf{X}||_{F}^{2}}+\sum\limits_{i=N+1}^{\min (m,n)}{{{\sigma }_{i}}({{\widetilde{\mathsf{\mathcal{P}}}}_{s}}\mathbf{X})},\] where $$$N$$$ is the rank of $$${{\widetilde{\mathsf{\mathcal{P}}}}_{s}}\mathbf{X}$$$, $$$m,n$$$ are the matrix size of $$${{\widetilde{\mathsf{\mathcal{P}}}}_{s}}\mathbf{X}$$$.
Results
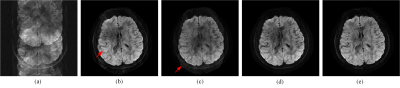
We conducted two in vivo brain DWI image reconstructions, including an 8-shot fully sampled DWI and a 4-shot DWI with partial Fourier sampling. The latter dataset is a good example of enabling faster DWI since the partial Fourier sampling is a common way to accelerate imaging and has been applied to multi-shot DWI in commercial MRI scanner. Our results were compared with two state-of-the-art navigator-free DWI image reconstruction methods, including the POCS-enhanced inherent correction of motion-induced phase errors (POCS-ICE)13 and multi-shot sensitivity encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS)14. Both MUSSELS and the proposed method avoid calculating the phase variations of different shots and try to reconstruct multi-shot images, and then combine them to a single one by a square root of sum of squares. All sensitivity maps were estimated from non-diffusion-weighted data by eigenvalue based iterative self-consistent parallel imaging reconstruction (ESPIRiT) 15.Figure 1 shows the reconstruction results of 8-shot fully sampled DWI. Directly inverse Fourier transformation induces severe aliasing artifacts (Figure 1 (a)). Much better images are obtained using POCS-ICE and MUSSELS but visible artifacts can be observed, as marked by red arrows in Figure 1. MUSSELS result looks dark in the center of image. While our result can effectively reconstruct the image without artifacts and with shaper edges than MUSSELS.
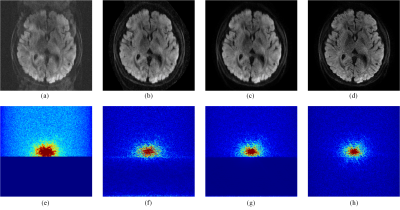
Figure 2 shows the reconstruction results of 4-shot partial Fourier sampled DWI with partial Fourier factor equals 55%. Directly inverse Fourier transformation induces strong aliasing artifacts. All other methods are able to recover artifact-free image. While POCS-ICE shows noisier than MUSSELS, MUSSELS cannot recover the uncollected part of partial Fourier sampled data at all, which cause blurred images using MUSSELS. Among all, our method leads to a sharper image and has the ability to recover the uncollected partial Fourier sampled data, indicating that the k-space conjugate symmetry property has inherently been exploited in our PLRHM model.
Conclusion
We propose a Phase-constrained Low-Rank Hankel Matrix (PLRHM) method to reconstruct magnetic resonance images in high-resolution multi-shot diffusion weighted imaging (DWI). Results show that our approach has the capability to provide reconstruction with less artifacts, sharper images compared with the state-of-the-art navigator-free DWI reconstruction methods, and recover partial Fourier data in accelerated DWI.Acknowledgements
This work was supported in part by National Key R&D Program of China (2017YFC0108700), National Natural Science Foundation of China (61571380, 61971361, 61871341, and 61811530021), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056), Science and Technology Program of Xiamen (3502Z20183053), and China Scholarship Council.
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
1. X. Zhang, D. Guo, Y. Huang, Y. Chen, L. Wang, F. Huang, and X. Qu, "Image reconstruction with Low-rankness and Self-consistency of k-space Data in Parallel MRI," arXiv preprint arXiv:1909.02846, 2019.
2. J. P. Haldar, "Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI," IEEE Transactions on Medical Imaging, vol. 33, no. 3, pp. 668-681, 2013.
3. K. H. Jin, D. Lee, and J. C. Ye, "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix," IEEE Transactions on Computational Imaging, vol. 2, no. 4, pp. 480-495, 2016.
4. G. Ongie and M. Jacob, "Off-the-grid recovery of piecewise constant images from few Fourier samples," SIAM Journal on Imaging Sciences, vol. 9, no. 3, pp. 1004-1041, 2016.
5. F. Lam, C. Ma, B. Clifford, C. L. Johnson, and Z. P. Liang, "High‐resolution 1H‐MRSI of the brain using SPICE: data acquisition and image reconstruction," Magnetic Resonance in Medicine, vol. 76, no. 4, pp. 1059-1070, 2016.
6. X. Qu, M. Mayzel, J. F. Cai, Z. Chen, and V. Orekhov, "Accelerated NMR spectroscopy with low‐rank reconstruction," Angewandte Chemie International Edition, vol. 54, no. 3, pp. 852-854, 2015.
7. X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, T. Agback, V. Orekhov, and Z. Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angewandte Chemie International Edition, DOI:10.1002/anie.201908162, 2019.
8. H. Lu, X. Zhang, T. Qiu, J. Yang, J. Ying, D. Guo, Z. Chen, and X. Qu, "Low rank enhanced matrix recovery of hybrid time and frequency data in fast magnetic resonance spectroscopy," IEEE Transactions on Biomedical Engineering, vol. 65, no. 4, pp. 809-820, 2017.
9. J. Ying, H. Lu, Q. Wei, J.-F. Cai, D. Guo, J. Wu, Z. Chen, and X. Qu, "Hankel matrix nuclear norm regularized tensor completion for N-dimensional exponential signals," IEEE Transactions on Signal Processing, vol. 65, no. 14, pp. 3702-3717, 2017.
10. J. Ying, J.-F. Cai, D. Guo, G. Tang, Z. Chen, and X. Qu, "Vandermonde factorization of Hankel matrix for complex exponential signal recovery—Application in fast NMR spectroscopy," IEEE Transactions on Signal Processing, vol. 66, no. 21, pp. 5520-5533, 2018.
11. Y. Hu, D. Zhang, J. Ye, X. Li, and X. He, "Fast and accurate matrix completion via truncated nuclear norm regularization," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 9, pp. 2117-2130, 2012.
12. T.-H. Oh, H. Kim, Y.-W. Tai, J.-C. Bazin, and I. So Kweon, "Partial sum minimization of singular values in RPCA for low-level vision," in Proceedings of the IEEE International Conference on Computer Vision, 2013, pp. 145-152.
13. H. Guo, X. Ma, Z. Zhang, B. Zhang, C. Yuan, and F. Huang, "POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI," Magnetic Resonance in Medicine, vol. 75, no. 1, pp. 169-180, 2016.
14. M. Mani, M. Jacob, D. Kelley, and V. Magnotta, "Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS)," Magnetic resonance in medicine, vol. 78, no. 2, pp. 494-507, 2017.
15. M. Uecker, L. Peng, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, "ESPIRiT — An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE meets GRAPPA," Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990-1001, 2014.
Figures