4344
NoiseFactors: Blind Denoising of dMRI via Randomized Factor Models1Intelligent Systems Engineering, Indiana University Bloomington, Bloomington, IN, United States, 2Psychological and Brain Sciences, Indiana University Bloomington, Bloomington, IN, United States
Synopsis
NoiseFactors is a probabilistic graphical model to suppress and remove additive noise in a single DWI image. It mitigates the issues caused by noise by preserving correlations in the signal components and suppressing the uncorrelated noise within local neighbourhoods. We solve the low-rank approximation problem by learning a best m-component approximation of a factor model. To do so we also introduce a novel flipped bi-crossvalidation to estimate the factor model. It outperforms the state-of-the-art PCA based methods such as Marchenko-Pastur PCA and Local PCA. The proposed method for denoising will be made available with an open-source implementation in DIPY.
Introduction
State-of-the-art research aiming to denoise DWI images as a post-processing step often makes use of the PCA1,2 as an underlying model to reconstruct the data from a smaller number of components. The PCA however approximates a low-rank matrix by having a common error variance variable per principal component3. It also reconstructs a low-rank approximation via principal components from noisy data (signal+noise). NoiseFactors mitigates this issue by having a specific uncorrelated error for each signal variable and preserving signal correlations5. The proposed approach generalizes probabilistic factor models and bi-crossvalidation for low rank approximations6. Factor modeling via exploratory factor analysis is an approach to causal discovery7, where the idea is to observe patterns of correlations in the observed signal via generative modeling. This enables statistical insight into the local neighbourhoods, which otherwise cannot be done in PCA. This method with the novel factor model and flipped bi-crossvalidation framework will be made available as a part of DIPY16.Methods
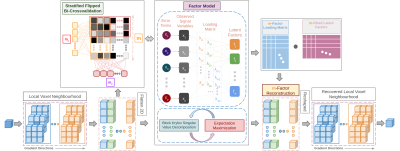
NoiseFactors takes a generative modeling approach to denoise the data using a graphical factor model. NoiseFactors sets up the denoising problem as a 2 phase latent variable learning and inference problem: 1) Given the noisy dataset, we learn the model parameters via EM based maximum likelihood estimation (MLE)8 and 2) Given the noisy signal and the estimated parameters (from step 1), infer the denoised signal. NoiseFactors makes use of the mean-field variational inference to maximize the evidence lower bounds (ELBO) for marginal log-likelihoods9. While the PCA based approaches to denoising aim to preserve the variance by minimizing the mean squared error, NoiseFactors aims to preserve the correlations among the image vectors (signal features) even in the reduced subspace4. As shown in Fig. 1, each of the latent factors are derived from the commonalities of the observed variables, where each variable has an uncorrelated noise. This noise is captured via variances specific to individual features in the low-rank approximation. Thus, we get an accurate estimation of the noise structure, independent of the size of the neighborhood chosen. NoiseFactors iterates between the SVD of the Factor Model and MLE for EM. We speed up the SVD by preconditioning it on the Block-Krylov subspace iterations as a linear-sketch random matrix10. We also propose a novel component estimation method for the factor model called stratified flipped bi-crossvalidation which extends the idea of bi-crossvalidation11 for factor models. NoiseFactors performs stratified k-fold cross-validation on the flattened 2D neighbourhood of the voxel once along the rows (estimate best-M1) and once along the columns (estimate best-M2). We compute the factor scores for each iteration of the process and choose M1 and M2 according to the number of components that maximize the scores and take the mean M. NoiseFactors chooses the best ‘M-Factors’ by performing flipped bi-crossvalidation against 1 through 27 (for fixed 3x3x3 local neighbourhood) factors. Lastly, we use the estimated optimal number of factors to construct the denoised matrix by simply taking a dot product between the M-Factor Loadings and M-transformed signal variables. NoiseFactors outperforms the state-of-the-art single image denoising methods such as LPCA1 and MP-PCA2 by taking a density estimation approach to causally explain common and specific variances associated with factor.Results
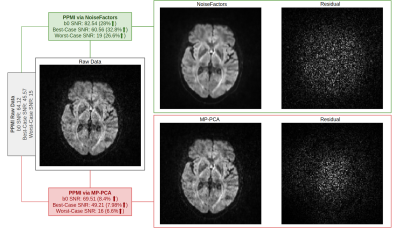
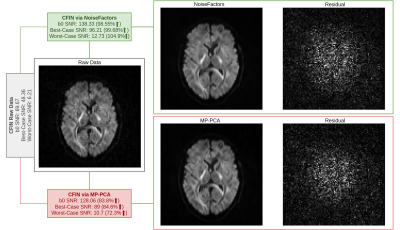
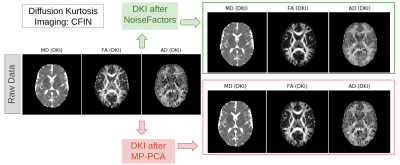
Our results show that NoiseFactors not only outperforms state-of-the-art denoising algorithms, but also improves subsequent microstructure estimation (demonstrated with DKI14). To evaluate the results, we compare against MP-PCA with qualitative and quantitative metrics (SNR). NoiseFactors strictly never removes any signal components from the data as is evident from the different types of data (single- and multi-shell) denoised. For SNR computation of the DWI, we use the corpus callosum to compute the best and worst case as a good estimate12,13 of SNR of the data. The proposed method is non-aggressive and does not remove signal structure from the data at any point. As shown in Fig. 2 and Fig. 3, NoiseFactors shows a significant improvement in the SNR as compared to MP-PCA. Our results indicate a ~30% increase for NoiseFactors and ~7% increase for MP-PCA on the PPMI dataset17 along with ~99% increase for NoiseFactors and ~80% increase for MP-PCA on CFIN dataset15). The model is completely automatic as the localized learning is unsupervised and aimed at preserving signal structure. As shown in Fig. 4, the proposed method improves the estimation of microstructural models from the data (here DKI) by reducing failure points (black voxels) occurring due to noise.Discussion
With our results we show that we mitigate the issue of noise with a factor model that can adapt to independent noise sources without any parameter tuning (eg: patch-size). NoiseFactors improves the results obtained from the DKI14 maps which otherwise breaks at multiple points due to the noise. We also show results on different types of data such as the CFIN15 and Parkinson’s PPMI17. The code of the algorithm will be made available in DIPY with different linear sketches for Randomized SVD. We also provide an implementation of Random Matrix Theory based OptShrink18 to iterate within Factor Model to perform a denoising SVD at each step. We will provide tools to perform causal inference on the noise distribution and perform robust statistical analysis on the latent factors in DIPY16.Acknowledgements
We would like to thank NIH R01EB027585 for supporting the PI and first author.References
[1] Manjón et. al. Diffusion Weighted Image Denoising Using Overcomplete Local PCA. PLoS ONE 8(9): e73021. https://doi.org/10.1371/journal.pone.0073021, 2013.
[2] Veraart, Jelle et al. Denoising of diffusion MRI using random matrix theory. NeuroImage vol. 142, doi:10.1016/j.neuroimage.2016.08.016, 2016.
[3] Jonathon Shlens, A Tutorial on Principal Component Analysis, ArXiv, 1404.1100, 2014.
[4] Johnson et. al. Applied Multivariate Statistical Analysis. Pearson, 2019.
[5] Dziuban et.al. When is a correlation matrix appropriate for factor analysis? Some decision rules. Psychological Bulletin, 81(6), 358-361, 1974.
[6] Madeleine, et. al. Generalized Low Rank Models. Foundations and Trends in Machine Learning: Vol. 9: No. 1, pp 1-118. http://dx.doi.org/10.1561/2200000055, 2016.
[7] Jöreskog et.al. Advances in factor analysis and structural equation models. Abt Books, 1979.
[8] Soares, et. al. Noise characterization of block-iterative reconstruction algorithms: II. Monte Carlo simulations. IEEE Trans Med Imaging. 24(1):112-21, 2005.
[9] Radford et.al. A view of the EM algorithm that justifies incremental, sparse, and other variants. MIT Press, Cambridge, MA, USA 355-368, 1999.
[10] Cameron Musco and Christopher Musco. Randomized block Krylov methods for stronger and faster approximate singular value decomposition. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1 (NIPS'15), 2015.
[11] Owen et. al. Bi-Cross-Validation for Factor Analysis. Statist. Sci. 31 , no. 1, 119--139. doi:10.1214/15-STS539, 2016.
[12] Descoteaux et. al. Multiple q-shell diffusion propagator imaging. Medical Image Analysis, 15(4), 603, 2011.
[13] Jones et. al. White Matter Integrity, Fiber Count, and Other Fallacies: The Dos and Don’ts of Diffusion MRI. NeuroImage, 73, 239, 2013.
[14] Jensen et. al. Diffusional Kurtosis Imaging: The Quantification of Non_Gaussian Water Diffusion by Means of Magnetic Resonance Imaging. Magnetic Resonance in Medicine 53: 1432-1440, 2005.
[15] Hansen et. al. Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Scientific Data 3: 160072 doi:10.1038/sdata.2016.72, 2016.
[16] Garyfallidis et. al. DIPY, a library for the analysis of diffusion MRI data, Frontiers in Neuroinformatics, vol. 8, p. 8, Frontiers, 2014.
[17] Kenneth et. al. The Parkinson Progression Marker Initiative (PPMI),Progress in Neurobiology, Volume 95, Issue 4, Pages 629-635, ISSN 0301-0082,https://doi.org/10.1016/j.pneurobio.2011.09.005, 2011.
[18] R. R. Nadakuditi. OptShrink: An Algorithm for Improved Low-Rank Signal Matrix Denoising by Optimal, Data-Driven Singular Value Shrinkage. IEEE Transactions on Information Theory, vol. 60, no. 5, pp. 3002-3018, doi: 10.1109/TIT.2014.2311661, 2014.
Figures