Purpose

As coordinate frame conventions may vary across scanners, file formats, and processing tools, the diffusion gradient orientations may end up rotated or permuted in a way that is inconsistent with the diffusion-weighted images. With these incorrect gradient orientations, the continuity of orientations across voxels will be disrupted, affecting, for example, subsequent tractography outcomes. Manual identification of the correct gradient orientations involves the tedious process of trying different combinations of permutations and sign flips, and inspecting the resulting orientation distribution functions (ODFs) or fiber tracts. Existing automated approaches^{1, 2} rely on explicit estimation of the fiber orientation distribution functions to determine the combination of orientation permutations, sign flips, and rotation that results in the highest across-voxel orientation continuity. In this abstract, we propose a fast correction method for gradient orientations that does not require model fitting and fiber tracking, allowing the correct gradient table to be determined within seconds.

Methods

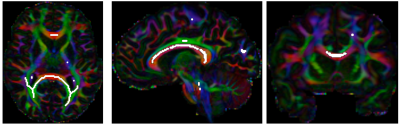
We identify the optimal combination of permutations and sign flips with the help of metric called cumulated orientation continuity (COC) across selected voxels. Only highly anisotropic voxels are selected for COC computation. Regions containing voxels with high relative spherical diffusion variance, computed directly from the diffusion-weighted images as described in Frank et al., 2001³, and identified and denoted by set $$$\Omega$$$. To select the feature region from the whole brain, we define an adaptive probability threshold $$$\lambda$$$ within the masked brain; i.e. a voxel is annotated as part of a feature region if its generalized fractional anisotropy has greater than $$$\lambda$$$. The adaptive threshold is computed as the sum of the mean and two standard deviations of the generalized fractional anisotropy across the masked brain. We then skeletonize⁴ $$$\Omega$$$ (see Figure 1) to form $$$\Omega_s$$$ for COC calculation.

We calculate the COC for each of the 24 possible combinations of orientation permutations and sign flips. The COC $$$\epsilon(\mathbf{G})$$$ for each gradient table $$$\mathbf{G}$$$ can be computed as $$$\epsilon(\mathbf{G}) = \frac{1}{|\Omega_s|} \sum_{\mathbf{p} \in \Omega_s} \min_{\mathbf{g}\in\mathbf{G}}(\frac{\phi(S_{\mathbf{p}}(\mathbf{g}))}{|{\mathcal{N}_{\mathbf{p}} }|})$$$, where $$$|{\mathcal{N}_{\mathbf{p}}}|$$$ is the number of neighborhood voxels connected to voxel $$$\mathbf{p}$$$, and $$$\phi(S_{\mathbf{p}}(\mathbf{g}))=\frac{1}{K_{\mathbf{p},\mathbf{g}}}\sum_{\mathbf{q} \in \mathcal{N}_{\mathbf{p}} \subset \Omega_s} W(\langle\mathbf{\hat{v}_{p,q}}, \mathbf{g}\rangle) S_{\mathbf{q}}(\mathbf{g})$$$, where $$$W(\langle\mathbf{\hat{v}_{p,q}}, \mathbf{g}\rangle)$$$ is a von Mises-Fisher directional probability distribution function (PDF)⁵ that is parameterized by the angular difference between $$$\mathbf{g}$$$ and $$$\mathbf{\hat{v}_{p,q}} = \frac{\mathbf{q} - \mathbf{p}}{\| \mathbf{q} - \mathbf{p} \|}$$$. $$$K_{\mathbf{p},\mathbf{g}} = \sum_{\mathbf{q} \in \mathcal{N}_{\mathbf{p}}\subset \Omega_s}W(\langle\mathbf{\hat{v}_{p,q}}, \mathbf{g}\rangle)$$$ is a normalization term. The correct configuration of the gradient orientations is identified by maximizing $$$\epsilon(\mathbf{G})$$$.

Materials

We evaluated our method using adult and infant data. Adult: Multi-shell dMRI data from the Human Connectome Project (HCP)⁶, $$$b=0, 1000, 2000, 3000\,\text{s}/\text{mm}^2$$$, voxel-size $$$1.25 \times 1.25 \times 1.25\,\text{mm}^3$$$. Infant: Multi-shell dMRI data of a 54-days-old infant from Baby Connectome Project (BCP)⁷. All data were corrected for motion and eddy-current and susceptibility induced geometric distortions.

Results

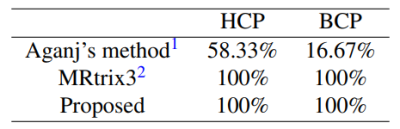
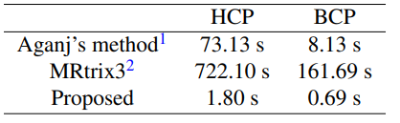
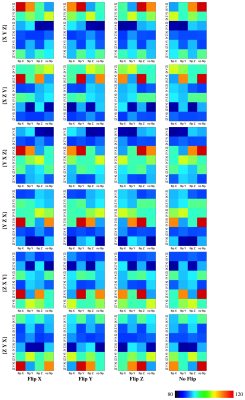
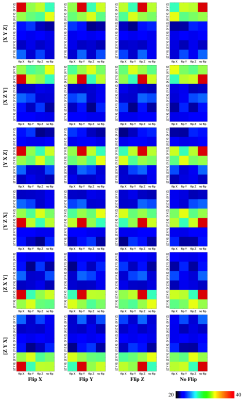
We evaluated our method with 24 gradient tables generated by permutating and sign-flipping the ground-truth table (top right in Figures 2 and 3). The vertical and horizontal axis labels denote the permutation and sign flipping performed on the ground-truth table. In Figures 2 and 3, the boxes with highest COC values correspond correctly to the permutations and sign flips required to undo the alteration of the ground-truth gradient tables. Table 1 shows that our method is significantly more accurate than existing methods (available online)^{1, 2} . The accuracy is computed by dividing the number of rightly corrected cases by 24. Table 2 indicates that our method is significantly faster. The computation time was evaluated using single-threading on a single CPU without considering data loading time.

Conclusion

Correcting for diffusion gradient orientations is an important step in dMRI processing, but is often done by trial and error and is hence time consuming. We have introduced a new fast model-free approach to automatically detecting the combination of orientation permutations and sign flips that corrects the gradient orientations.

Acknowledgements

This work was supported in part by NIH grants (NS093842 and 1U01MH110274) and the efforts of the UNC/UMN Baby Connectome Project Consortium.