4336
Evaluation of simple acceleration strategy for advanced neural diffusion models based on half q-space under-sampling1Shanghai University of Medicine & Health Sciences, Shanghai, China, 2MR Scientific Marketing, Siemens Healthcare, Shanghai, China, 3Shanghai Key Laboratory of Magnetic Resonance, East China Normal Univeristy, Shanghai, China
Synopsis
Advanced diffusion models such as NODDI, MAP-MRI are of high interests in brain research, but suffer from long acquisition time. Advanced under-sampling scheme were reported in previous studies for acceleration but are not commercially available. This study evaluates a simple and commercial available under-sampling scheme using the symmetric property of q-space, which could accelerate the acquisition by 2 fold. Results showed that it did not significant sacrifice the accuracy of quantitative maps. In addition, a symmetrically data copy step is needed to improve the estimation accuracy for both MAP-MRI and NODDI models.
Introduction
Diffusion-weighted MRI (DWI) is a powerful technique to probe the tissue microstructural changes and provide a range of quantitative scalar metrics across the whole brain. Diffusion tensor imaging (DTI) has been widely used to previous studies. Recently advanced diffusion models were proposed, such as Neurite orientation dispersion and density imaging (NODDI) and Mean apparent propagator (MAP)-MRI, which can reflect complicated tissue characteristics, such as the degree of fanning of fibers, the axonal density, the diffusion anisotropy and the non-Gaussian character of the three-dimensional diffusion process1. However, normally a large dataset is needed for these models with multiple b-value and diffusion gradient directions, result in long scan time hardly acceptable in clinical application. Previous studies reported that multiband2 and advanced under-sampling schemes3,4 could significantly reduce the scanning time, while the under-sampling schemes could bias the parameters. Besides this drawback, the advanced under-sampling schemes are not available in commercial MR scanner, thus making it difficult for widely application in clinical routine. In this study, we evaluate a simple half-under-sampling scheme (2 fold acceleration) using the symmetrical property of gradient direction distribution in conventional diffusion spectrum imaging (DSI) technique, which is becoming commercially available recently. Its influence for quantitative parameters of NODDI, MAP-MRI models was investigated.Methods
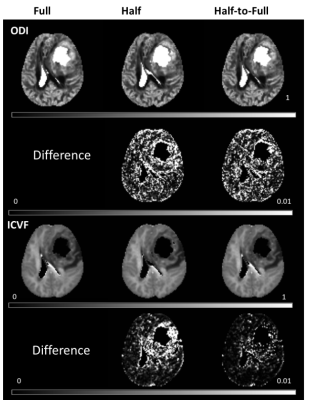
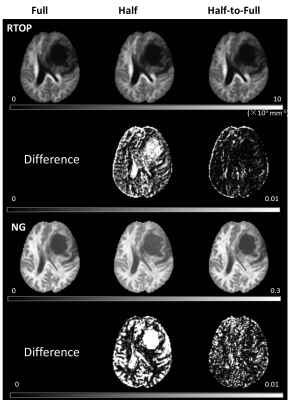
Two patients with brain tumor were enrolled and underwent MRI scanning using a 3T MR scanner (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany). The DSI data were acquired using a fully Cartesian q-space grid scheme. The DSI parameters were as follows: TR/TE = 3900/72 ms, FOV = 220 × 220 mm2, matrix = 128 × 128, slice thickness = 2 mm, in-plane acceleration factor = 2, slice acceleration factor = 2, diffusion time δ/Δ = 15.9/35.0 ms, bmax = 3000 s/mm2, two b=0 data and 98 DWI data with a radius of three samples, total scan time = 6 min 42 s. A symmetric q-space scheme is used here.Three q-space sampling schemes were compared in the study: 1) Full sampled data with all 98 directions, denotes as Full; 2) a half-sphere under-sampled data with 49 non-parallel directions, denotes as Half; 3) a half-sphere under-sampled data with 49 non-parallel direction, and the other half data are symmetrically copied from the acquired data, denotes as Half-to-Full. Eddy currents distortion and subject motion was corrected using bneddy tool of DiffusionKit software5. The NODDI and MAP-MRI parameters from the three sampling schemes were calculated using an in-house developed software called NeuDiLab, which is based on an open-resource tool DIPY (Diffusion Imaging In Python, http://nipy.org/dipy). The NODDDI parameters included intracellular volume fraction (ICVF) and orientation dispersion index (ODI). The MAP-MRI parameters included the return to the origin probability (RTOP) and Non-Gaussianity (NG). The percent of square coefficient of variation (CV) was used to assess the differences for three reconstruction schemes.
Results
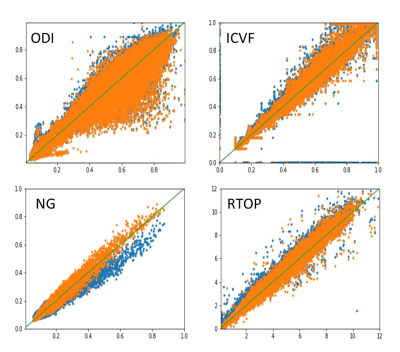
Figure 1 shows parameter maps from the NODDI model and their corresponding CV for one patient using three sampling schemes, and Figure 2 shows the results from MAP-MRI model. Refer to Full scheme, the Half-to-Full scheme showed smaller CV than the Half scheme for all parameters of MAP-MRI model. While for NODDI model, similar CV was found for Half and Half-to-Full scheme, and Half-to-Full scheme showed slightly smaller CV than Half scheme in ICVF maps, especially in the around regions of tumor. Figure 3 shows scatter plots of quantitative parameters from Full scheme against Half or Half-to-Full scheme on voxel-by-voxel basis for the whole brain. The parameter NG showed a obvious bias for Half scheme, while Half-to-Full scheme showed no bias against the Full scheme.Discussion
In this study, the quantitative parameters of NODDI and MAP-MRI models were compared among three diffusion sampling schemes. The results found that Half-to-full scheme outperformed the Half scheme with smaller difference of quantitative parameters referred to the Full scheme, especially for the MAP-MRI parameters. It means that the MAP-MRI model estimation were more sensitive to the DWI sampling schemes than NODDI metrics, which =is consistent with the findings of previous studies3,4. In addition, the symmetric data copying step can effectively reduce estimation error.To conclude, this study showed that the acquisition time of advanced diffusion models could be efficiently reduced by using half q-space sampling scheme in combination with symmetrically data copying to fill the other half data. Thus, this acceleration scheme could be applied widely in clinical routine or for special patient group such as children.
Acknowledgements
No acknowledgement found.References
1. Ozarslan E, Koay CG, Shepherd TM, et al. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. Neuroimage, 2013;78:16-32.
2. Bernstein AS, Chen N, Trouard TP. Bootstrap analysis of diffusion tensor and mean apparent propagator parameters derived from multiband diffusion MRI. Magn Reson Med, 2019; 82:1796-1803.
3. Olson DV, Arpinar VE, Muftuler LT. Optimization of q-space sampling for mean apparent propagator MRI metrics using a genetic algorithm. NeuroImage, 2019; 199: 237-244.
4. Hutchinson EB, Avram AV, Irfanoglu MO, et al. Analysis of the effects of noise, DWI sampling, and value of assumed parameters in diffusion MRI models. Magn Reson Med, 2017; 78: 1767-1780.
5. Sangma Xie, Liangfu Chen, Nianming Zuo and Tianzi Jiang, DiffusionKit: A Light One-Stop Solution for Diffusion MRI Data Analysis, Journal of Neuroscience Methods, 2016; 273: 107-119.
Figures