4329
Acceleration of multidimensional diffusion MRI data acquisition and post-processing using convolutional neural networks
Yuan Zheng1, Tao Feng1, Sirui Li2, Wenbo Sun2, Qing Wei3, Samo Lasic4, Danielle van Westen5, Karin Karin Bryskhe4, Daniel Topgaard4,5, and Haibo Xu2
1UIH America, Houston, TX, United States, 2Zhongnan Hospital of Wuhan University, Wuhan, China, 3United Imaging Healthcare, Shanghai, China, 4Random Walk Imaging, Lund, Sweden, 5Lund University, Lund, Sweden
1UIH America, Houston, TX, United States, 2Zhongnan Hospital of Wuhan University, Wuhan, China, 3United Imaging Healthcare, Shanghai, China, 4Random Walk Imaging, Lund, Sweden, 5Lund University, Lund, Sweden
Synopsis
Multidimensional diffusion MRI (dMRI) is a powerful tool that even in its simplest form provides more detailed microstructural information than conventional dMRI, such as microscopic anisotropy (µFA) unconfounded by orientation dispersion. However, it requires multiple diffusion encoding modes (usually directional and isotropic encodings) and, for the more advanced versions, prolonged scan and post-processing times. We proposed using convolutional neural networks (CNN) to accelerate multidimensional dMRI data acquisition and analysis, and have demonstrated that satisfactory µFA maps can be generated in real-time with only 50% of the encodings, which might help to better adapt multidimensional dMRI to clinical practices.
Introduction
Multidimensional diffusion MRI (dMRI)1 is a novel imaging modality that provides more detailed microstructural information than conventional dMRI, for instance independent quantification of microscopic fractional anisotropy (µFA) and orientation dispersion2 which are two fundamentally different properties that are entangled in conventional methods. However, in addition to conventional directional encoding, multidimensional dMRI requires more advanced diffusion encoding modes such as isotropic encoding2, requiring somewhat longer scan times. While simple estimation of µFA with the generalized cumulant inversion3 requires no more time than for conventional DTI analysis, more advanced post-processing relying on Monte Carlo inversion currently is too time-consuming for real-time diagnosis.4 Both the long acquisition and analysis time may limit the clinical use of the more advanced forms of multidimensional dMRI.Great potential has been demonstrated using convolutional neural networks (CNN) with deep learning in many aspects of MRI. In this study, we trained a CNN model using only half of the total diffusion encodings to predict µFA maps. High quality µFA maps were generated in real time, demonstrating the possibility of using CNN to significantly accelerate multidimensional dMRI data acquisition and post-processing.
Methods
Eighty-five patients with glioma, meningioma and some other brain diseases were included in this study. MRI scans were performed on a uMR 790 3.0 T scanner (United Imaging Healthcare, Shanghai, China) with a 24-channel head coil. The multidimensional dMRI sequence has 80 diffusion gradient encodings total, including 40 directional and 40 isotropic (Fig.1). For both encoding schemes, images were acquired at a b=100, 700, 1400, 2000 s/mm2, with 6, 6, 12, 16 directions or averages. Imaging parameters were identical for both kinds of encoding as detailed in Fig.1 caption. The number of slices were chosen to cover the whole brain, and the total scan time was approximately 5 min. Images were analyzed using the procedure described by Lasič to extract µFA2, assuming a Gamma distribution of the diffusivity.Slices below the nasal cavity were excluded to avoid EPI artifact caused by the complex air-tissue boundaries, and a total of 1444 slices were included in CNN training (1155) and test (289). We retrospectively undersampled both directional and isotropic encodings at each b value by 50% while aiming to maintain a relatively uniform direction distribution. The 40 diffusion encodings left were used as the network input (112×112×40) and the µFA maps generated from all the 80 encodings with the Gamma model were used as the output (112×112) for model training. Structure of the CNN is shown in Fig.2. Eight convolutional layers were included. The number of channels for the layers were 80,120,180,180,120,60,30 and 1. A 3×3 filter was used for all layers. Leaky rectified linear units (ReLU) were applied for all layers except the last one, which was followed by conventional ReLU activation. The normalized squared error was used as the loss function and Adam5 was used as the optimizer. The CNN was implemented using Tensorflow. Data augmentation including horizontal/vertical flips and rotation were applied, and each batch contained 9 slices. The number of epochs for model training was determined using 10-fold cross-validation of the training set. The model was then trained on the full training dataset and evaluated on the test dataset.
Results
The training and validation loss during cross validation were shown in Fig.3. Both losses became flat after 200 iterations with no major difference. The epoch # for final model training was thus chosen to be 200. The model performance was evaluated on the test dataset, and the normalized squared error was ~2.2%. Fig.4a shows the FA map of a meningioma case calculated using directionally encoded images with the DTI model. Low FA value is ambiguous since it could be caused either by orientation dispersion or lack of microanisotropy. On the other hand, the basic implementation of multidimensional dMRI showed elevated µFA of the tumor (Fig.4b,c), revealing strong subvoxel microanisotropy (Fig.4d). The µFA maps reconstructed with the conventional method and the proposed CNN approach showed similar results. The former took 80 diffusion encodings (5 min scan time) and 8 min for data analysis on a intel 8-core 3.4 GHz CPU, while the latter took only 40 encodings (2.5 min scan time) and under 2 sec to generate the µFA map with a Nvidia GTX960 GPU.Discussion
We acquired 80 diffusion encodings in this study because of clinical scan time concerns, while some other multidimensional dMRI studies used larger numbers of diffusion encodings4. Therefore our µFA maps calculated using the conventional method were slightly noisy. However, they were still used for model training and evaluation. In this case the normalized loss does not accurately reflect the model performance, since denoising effect of the CNN makes the prediction deviate from the “gold standard” but is desired.Conclusion
Multidimensional dMRI is a powerful tool that even in its simplest incarnation provides more detailed microstructural information than conventional dMRI. However, the more advanced versions require prolonged scan and post-processing time. We proposed using CNN to accelerate multidimensional dMRI data acquisition and analysis, and have demonstrated that satisfactory µFA maps can be generated in real-time with only 50% of the encodings, which might help to better adapt this technique to clinical settings.Acknowledgements
Data collection was approved by the Wuhan hospital ethics committee and with written informed consent from all participants. This work was financially supported by the national key research and development plan of China (2017YFC0108803), the Swedish Foundation for Strategic Research (AM13-0090, ITM17-0267) and the Swedish Research Council (2018-03697). Daniel Topgaard owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods.References
- D. Topgaard. Multidimensional diffusion MRI. J Magn. Reson. 275:98-113 (2017).
- S. Lasič et.al., Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Front. Physics. Feb 27 (2014).
- Sjölund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin C-F, Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157-168.
- Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell L, Kubicki M, Topgaard D, Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 2016;135:345-362.
- Topgaard D. Diffusion tensor distribution imaging. NMR Biomed 2019;32:e4066.
- F. Szczepankiewicz et.al., The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage. 142:522-532 (2016). D. P. Kingma et.al., Adam: A method for stochastic optimization, arXiv Prepr. arXiv1412.6980, 2014.
Figures
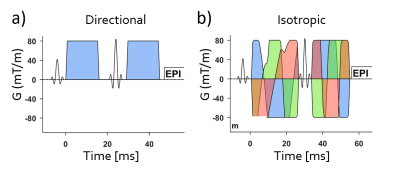
Figure 1: Conventional dMRI uses directional encoding a) with multiple directions. Multidimensional
dMRI requires both directional and isotropic b) encodings to provide more detailed
microstructural information, such as the microanisotropy. The isotropic encoding
was performed with a numerically optimized waveform3. Identical imaging parameters were used for directional
and isotropic measurements, including: TR/TE = 3750/85 ms, FA = 90°,
thickness = 4 mm, FOV = 224×224 mm, matrix = 112×112, bandwidth = 1560
Hz/pixel, partial Fourier factor = 0.75, parallel imaging factor = 2.
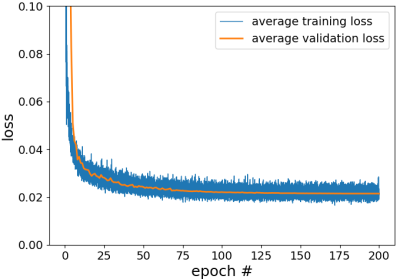
Figure 2: The training and validation losses during 10-fold cross-validation. After
200 epochs, both losses became stable and there is no major difference between
them.
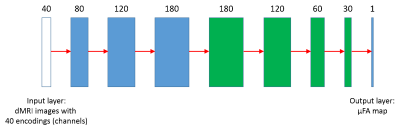
Figure 3: Structure of the CNN. The network has 4 convolution layers (blue) and 4
deconvolution layers (green). The number of channels is first expanded and then
gradually shrinked to 1, while the image dimension is kept at 112 × 112
throughout. Leaky-RELU is applied to all layers after convolution except the
output layer, which is followed by conventional RELU activation.
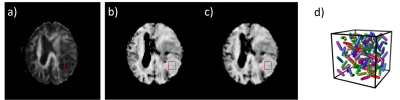
Figure 4: The
FA map of a meningioma case calculated using the conventional directional data
with a DTI model is shown in a). The µFA maps generated using
the Gamma model (80 encodings) and the CNN (40 encodings) are similar and shown
in b) and c) respectively. In the 9 × 9 ROI centered on the tumor, FA = 0.14 ±
0.04, µFA = 0.73 ± 0.05 and 0.70 ± 0.06 in b) and c). The low FA only indicates
there is no macroscopic anisotropy, while the high µFA reveals strong
microscopic anisotropy, as illustrated schematically in d).