4328

Correction for the influence of transmit-inhomogeneity in DW-SSFP on signal and ADC estimates in whole post-mortem brains at 7T
Benjamin C Tendler1, Sean Foxley2, Moises Hernandez-Fernandez3, Michiel Cottaar1, Olaf Ansorge4, Saad Jbabdi1, and Karla Miller1
1Wellcome Centre for Integrative Neuroimaging, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Department of Radiology, University of Chicago, Chicago, IL, United States, 3Centre for Biomedical Image Computing and Analytics, University of Pennsylvania, Philadelphia, PA, United States, 4Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom

Synopsis

Diffusion-weighted steady-state free precession (DW-SSFP) generates high SNR diffusivity estimates in whole, post-mortem human brains. Improved estimates at 7T has motivated its use at ultra-high field. However, the DW-SSFP signal has a strong dependence on flip angle. This translates into both variable signal amplitude and diffusion contrast. At 7T, transmit-($$$B_{1}^{+}$$$) inhomogeneity leads to $$$B_{1}^{+}$$$-dependent SNR and ADC estimates. Previous work corrected for $$$B_{1}^{+}$$$-inhomogeneity by acquiring DW-SSFP datasets at two flip angles. Here, this approach is extended, utilising the full Buxton model of DW-SSFP to model non-Gaussian diffusion. A noise-floor correction and signal weighting are also incorporated to improve diffusivity estimates.

Introduction

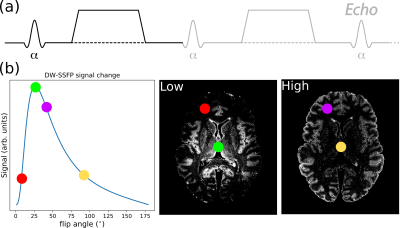
Post-mortem diffusion imaging of whole human brains allows validation of the origins of diffusion contrast through comparisons with microscopy. However, death and fixation leads to tissue samples characterised by a short T2 and low diffusivity1,2, resulting in low SNR when using conventional diffusion imaging sequences. Diffusion-weighted steady-state free precession (DW-SSFP) (Fig. 1a) is a fast, highly SNR-efficient diffusion imaging method that achieves strong diffusion weighting in clinical scanners with limited gradient strengths3. Previous work4,5 has demonstrated the potential of DW-SSFP to obtain high-SNR diffusivity estimates in whole human brains. Further SNR gains have been reported at 7T compared to 3T6.
However, in order to fully take advantage of the improved SNR and resolution at 7T, we need to overcome the challenge of transmit-($$$B_{1}^{+}$$$) inhomogeneity. This becomes particularly problematic in DW-SSFP, as both the signal (Fig. 1b) and diffusion attenuation (Fig. 2a) are flip angle dependent7. One approach that has been proposed to address $$$B_{1}^{+}$$$-inhomogeneity is to acquire DW-SSFP datasets at two flip angles8, with the goal of combining these two datasets to remove the spatially varying contrast.
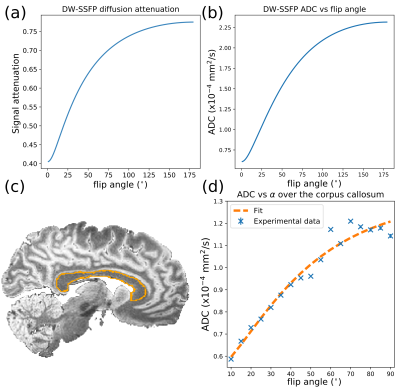
Recently, we have proposed a theoretical framework9 to model non-Gaussian diffusion from DW-SSFP data acquired at two or more flip angles (Fig. 2). In non-Gaussian diffusion regimes, the ADC is strongly dependent on flip angle (Fig 2c and 2d). Interestingly, this framework also provides a principled way to combine measurements at multiple flip angles, by synthesising an ADC corresponding to a chosen b-value. This approach simultaneously addresses $$$B_{1}^{+}$$$-inhomogeneity and the lack of a well-defined b-value in DW-SSFP.
The work presented here builds on previous work8,10,11 in several distinct ways. Firstly, we incorporate the full Buxton model7 of DW-SSFP, where previous work used the two-transverse period approximation11. Secondly, we have included a noise-floor correction to reduce the bias on diffusivity estimates in conditions of low signal12. Finally, the fitting cost function is weighted by the DW-SSFP signal amplitude to improve the robustness of the parameter fits.

Methods

Whole, fixed post-mortem brains were scanned in a whole-body 7T system (Siemens, Nova-Medical 1TX/32RX coil). For each brain, DW-SSFP data (q=300cm-1, TE=21ms, TR=28ms, 120 directions, resolution=0.85x0.85x0.85mm3) were acquired at two flip angles (24o and 94o). T1, T2 and B1 maps (dependencies of the DW-SSFP signal model7) were also acquired. For more information of the full acquisition and pre-processing, see10,13.
The DW-SSFP datasets were fitted with a diffusion tensor model incorporating the full Buxton signal model7 in cuDIMOT14. The model was designed to fit to the DW-SSFP data acquired at both flip angles simultaneously to obtain a shared set of eigenvectors and flip-angle-dependent eigenvalues. This fitting was weighted by the signal amplitude to account for the available SNR at each flip angle. A noise-floor term was incorporated into the fit to reduce bias in low signal regions12,15, fitting to: $$S=(S_{SSFP}^{2}+S_{nf}^{2})^{\frac{1}{2}},\tag{1}$$ where $$$S_{SSFP}$$$ is the DW-SSFP signal from the full Buxton model and $$$S_{nf}$$$ is the noise-floor (estimated from the background signal). The unique set of eigenvalues obtained at each flip angle were subsequently extrapolated to a single SNR-optimal effective b-value, determined as $$$b_{eff}=7600s/mm^2$$$ from simulation. This extrapolation is based on a gamma distribution of diffusivities16 embedded in the full Buxton model of DW-SSFP, evaluated via numerical integration9.

Results and Discussion

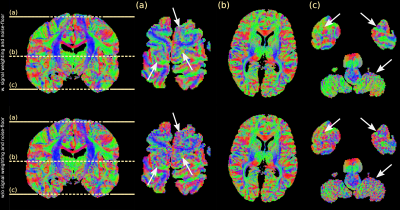
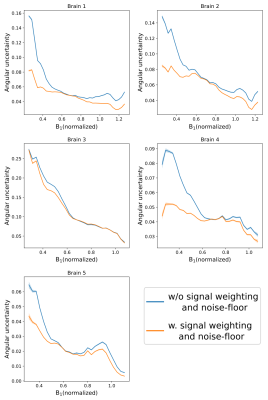
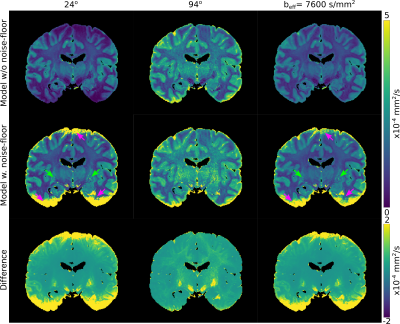
Figure 3 displays the principal-diffusion-direction (PDD) eigenvector estimates obtained from our dual-flip angle approach. By incorporating signal weighting and a noise-floor correction, we observe clear improvements in coherence in the PDD estimates in the superior and inferior regions of the brain, areas associated with very low $$$B_{1}^{+}$$$. Reductions in angular uncertainty (Fig. 4) are most apparent in areas of low/high $$$B_{1}^{+}$$$, associated with low SNR in the 24o/94o datasets respectively. Reduced angular uncertainty is generally predictive of improved tractography.
Figure 5 displays the L1 maps for a single brain. The ADC estimates at 94o are generally higher than at 24o, consistent with a model of non-Gaussianity (Fig. 2). At $$$b_{eff}=7600s/mm^2$$$, our maps display more homogeneous contrast across the brain, with similar contrast to the 24o dataset (from simulation, $$$b_{eff}=7600s/mm^2$$$ corresponds to a flip angle of 20o-24o).
By incorporating a noise-floor correction, we improve the diffusivity estimates by reducing the bias in some regions of tissue12 (visible in the difference maps). This is most notable at 24o in the deep grey matter (green arrows). However, in areas of very low signal, our noise floor correction is unable to rectify the ADC estimates, leading to spuriously high values (pink arrows). Prior to noise floor correction, these regions are characterised by very low ADCs. Though these diffusivity estimates are biased before (low ADC) and after (high ADC) correction, the high ADC values in our noise-floor corrected data are fundamentally incompatible with our framework9 (Figure 2), leading to artefacts which propagate into the final $$$b_{eff}=7600s/mm^2$$$ maps.

Conclusion

By acquiring DW-SSFP data at two flip angles, we simultaneously account for variable SNR and ADC estimates induced by transmit-inhomogeneity. Signal weighting provides improved coherence and a reduced angular uncertainty in eigenvalue estimates. ADC estimates derived at a single SNR optimal effective b-value display more homogeneous contrast. Future work will investigate approaches to reduce the bias in ADC estimates in regions of very low signal.

Acknowledgements

This study was funded by a Wellcome Trust Senior Research Fellowship (202788/Z/16/Z) and Medical Research Council grant MR/K02213X/1 and MR/L009013/1. Brain samples was provided by the Oxford Brain Bank (BBN004.29852). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).

References

1. Shepherd TM, Thelwall PE, Stanisz GJ, Blackband SJ. Aldehyde fixative solutions alter the water relaxation and diffusion properties of nervous tissue. Magn Reson Med. 2009. doi:10.1002/mrm.21977

2. D’Arceuil H, de Crespigny A. The effects of brain tissue decomposition on diffusion tensor imaging and tractography. Neuroimage. 2007. doi:10.1016/j.neuroimage.2007.02.039

3. McNab JA, Miller KL. Steady-state diffusion-weighted imaging: Theory, acquisition and analysis. NMR Biomed. 2010. doi:10.1002/nbm.1509

4. McNab JA, Jbabdi S, Deoni SCL, Douaud G, Behrens TEJ, Miller KL. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage. 2009. doi:10.1016/j.neuroimage.2009.01.008

5. Miller KL, McNab JA, Jbabdi S, Douaud G. Diffusion tractography of post-mortem human brains: Optimization and comparison of spin echo and steady-state free precession techniques. Neuroimage. 2012. doi:10.1016/j.neuroimage.2011.09.054

6. Foxley S, Jbabdi S, Clare S, et al. Improving diffusion-weighted imaging of post-mortem human brains: SSFP at 7T. Neuroimage. 2014. doi:10.1016/j.neuroimage.2014.08.014

7. Buxton RB. The diffusion sensitivity of fast steady‐state free precession imaging. Magn Reson Med. 1993. doi:10.1002/mrm.1910290212

8. Foxley S, Jbabdi S, Clare S, Miller K. Correcting for B1 inhomogeneities in post-mortem DWSSFP human brain data at 7T using multiple flip angles. In: Proc. Intl. Soc. Mag. Reson. Med. Vol 22. ; 2014:4438.

9. Tendler BC, Foxley S, Cottaar M, Jbabdi S, Miller K. Modelling an equivalent b-value in diffusion-weighted steady-state free precession. arXiv 191101093. 2019.

10. Tendler BC, Jbabdi S, Foxley S, et al. Development of a diffusion-weighted SSFP acquisition and processing pipeline to quantify the diffusion properties of the post-mortem ALS brain at 7T. In: Proc. Intl. Soc. Mag. Reson. Med. Vol 26. ; 2018:1027.

11. Tendler BC, Jbabdi S, Foxley S, et al. Disentangling diffusion-weighted SSFP: ADC estimates in terms of an effective diffusion time. In: Proc. Intl. Soc. Mag. Reson. Med. Vol 27. ; 2019:0551.

12. Jones DK, Basser PJ. “Squashing peanuts and smashing pumpkins”: How noise distorts diffusion-weighted MR data. Magn Reson Med. 2004. doi:10.1002/mrm.20283

13. Pallebage-Gamarallage M, Foxley S, Menke RAL, et al. Dissecting the pathobiology of altered MRI signal in amyotrophic lateral sclerosis: A post mortem whole brain sampling strategy for the integration of ultra-high-field MRI and quantitative neuropathology. BMC Neurosci. 2018;19(1). doi:10.1186/s12868-018-0416-1

14. Hernandez-Fernandez M, Reguly I, Jbabdi S, Giles M, Smith S, Sotiropoulos SN. Using GPUs to accelerate computational diffusion MRI: From microstructure estimation to tractography and connectomes. Neuroimage. 2019. doi:10.1016/j.neuroimage.2018.12.015

15. Gudbjartsson H, Patz S. The rician distribution of noisy MRI data. Magn Reson Med. 1995;34(6):910-914. doi:10.1002/mrm.1910340618

16. Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ. Model-based analysis of multishell diffusion MR data for tractography: How to get over fitting problems. Magn Reson Med. 2012. doi:10.1002/mrm.24204

Figures

Figure 1: (a) DW-SSFP consists of a single RF pulse and diffusion gradient per TR. Transverse magnetisation is not spoiled at the end of each TR. A short TR leads to magnetization that persists and evolves over multiple TRs, generating a signal which is very sensitive to flip angle (b – left). At low flip angles (b – middle), $$$B_1^+$$$-inhomogeneity leads to high signal at the brain centre, low signal near the edge. High flip angle datasets (b – right) have the opposite distribution. We can utilize these two datasets to obtain high signal across the whole brain. (b) shows signal change (CNR).

Figure 2: DW-SSFP diffusion attenuation is dependent on the flip angle (a). In non-Gaussian systems, this will give rise to flip angle dependent ADC estimates (b). From experimental DW-SSFP data acquired at multiple flip angles in a post-mortem brain (c), we observe an increased ADC with flip angle over the corpus callosum (d – blue crosses). By fitting a model of non-Gaussian diffusion which is able to explain this variation in ADC (d – orange line), we can simulate the ADC at any flip angle. Alternatively, using our framework9, ADCs can be defined in terms of an effective b-value.

Figure 3: PDD estimates for a single post-mortem brain with (top) and without (bottom) signal-weighting and a noise-floor correction. Here, three different axial slices (a,b and c) are shown (denoted in the coronal slice on the left). We observe that by incorporating signal weighting and a noise-floor correction, we generate improved coherence estimates, particularly within superior (a) and inferior (c) regions of the brain (white arrows). These areas are associated with very low $$$B_{1}^{+}$$$ and low signal in the 24o dataset.

Figure 4: Angular uncertainty estimates of the PDD over white matter as a function of $$$B_{1}^{+}$$$. By incorporating signal weighting and a noise-floor correction (orange lines), we observe a reduction in the angular uncertainty, most notable in areas of low/high $$$B_{1}^{+}$$$, associated with low signal in the 24o/94o datasets. Error bars denote the standard error in the PDD angular uncertainty, but are generally too small to be easily visible.

Figure 5: L1 maps in a single brain with/without noise-floor correction. ADC estimates are generally higher at 94o vs 24o, consistent with Fig. 2b. By adding in a noise-floor correction, we reduce the bias on ADC estimates in some areas (visible in the difference maps). This is most notable in deep grey matter (green arrows), where ADC estimates are more consistent with the surrounding tissue. However, in areas of very low signal, the noise-floor correction generates spuriously high ADC estimates (pink arrows), leading to artefacts which propagate into $$$b_{eff}=7600s/mm^2$$$.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
4328