4320
Isotropic sampling for skewed encoding: novel rotation schemes for non-axisymmetric encoding objects in diffusion MRI1Harvard Medical School, Boston, MA, United States, 2Brigham and Women's Hospital, Boston, MA, United States
Synopsis
In this work we propose novel sampling schemes for diffusion MRI required for encoding with objects with more than one directional axis. The presented solution is general and suitable for both axisymmetric and non-axisymmetric encoding schemes. An important feature of the presented sampling schemes is that they can be interleaved and be complimentary. This means that any combination of them can be used to define an isotropic sampling scheme with number of samples: (15, 30, 45, 60, 75, 90).
Introduction
The quest of finding the optimal sampling scheme for diffusion MRI is still active after decades of research on this topic. Early work for single diffusion encoding focussed on electrostatic repulsion to define isotropically distributed directions of diffusion encoding [Bak97, Jones99], and later extended to multiple shells [Caruyer13]. Here we turn our attention to sampling schemes required for encoding with objects with more than one directional axis, such as b-tensors encoding [Westin16], or any encoding waveform that has non-isotropic features, such as double diffusion encoding [Shemesh16]. The presented schemes are general, but they are especially important when using b-tensors encoding were the three eigenvalues are unique. For such diffusion encoding, it is not sufficient to sample the directions of one of the axes of the b-tensor isotropically, but all three axes have to be distributed isotropically independently and simultaneously. In certain cases, in the Gaussian regime and using diffusion encoding with axisymmetric b-tensors, it is sufficient to distribute the axis of symmetry isotropically since any rotation around that axis will not affect the encoding, and thus the system is automatically isotropic for this case. For all other cases, distributing complete coordinate systems isotropically is preferred in order to minimize the effect of directional biases.Theory
We are here describing two different principles to generate isotropically distributed coordinate systems:The first principle is based on defining local coordinate systems based on the midpoints of isotropically distributed edges. The coordinate system is defined by the three vectors 1) along the edge, 2) from the midpoint to the center, and 3) the crossproduct between then defining a normal to the edge. We exemplify this method using the geometries of the icosahedron and the dodecahedron, expanding on the sampling schemes presented in [Westin16]. Both the icosahedron and the dodecahedron has 30 edges. These edges are crossing at a right angle, and are sharing its midpoints.
The second principle is based on defining isotropically distributed points, and define an orthogonal plane in which to distribute equidistant orientations, and the cross product between each of them to define a third direction for each pair. An example of this is to use the set of sampling directions that are defined by the corners of the icosahedron. We can define the major axis of each coordinate system by the corners of the icosahedron. We have 12 such corners. From each corner, there are 5 edges. This lets us define 5 directions from each of the 12 corners. By projecting these direction to the plane orthogonal to major direction, this lets us defines 12x5=60 orthogonal coordinate systems. Because of the symmetries of the icosahedron, this set can be decomposed into two complementary sets of 6x5=30 directions. This sampling scheme is closely related to the double diffusion encoding scheme proposed in [Jespersen13]. Although only two directions are defined in a scheme for double diffusion encoding, the third direction can trivially be defined as the cross product between the two.
Results
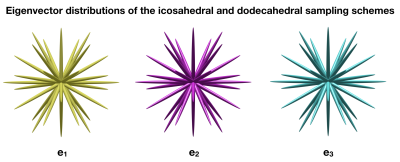
Figure 1 illustrates the sampling principle based on defining sampling coordinate systems based on midpoints of isotropically distributed edges. We are here using the icosahedron and dodecahedron to define 15 + 15 different "orientations". An interesting fact with this sampling scheme is that all these 30 orthogonal coordinate system share the axes of the 15 main directions. This means that the distribution of the eigenvectors in b-tensor encoding, is the same for all eigenvectors. The blue and red plots show ellipsoids illustrating local coordinate systems, and can also be viewed as b-tensors with distinct eigenvalues.Figure 2 illustrates the distributions of the eigenvectors of the icosahedron and dodecahedron midpoint sampling schemes. This sampling scheme defines 15 + 15 local coordinates systems. When performing b-tensor encoding, a tensor will be defined and rotated to each of these coordinate system. By calculating the eigenvectors of these rotated b-tensors we can see that the proposed sampling has the same isotropic distribution in each of the three axes independently and simultaneously.
Discussion and conclusions
In this work, we propose novel sampling schemes required for encoding with objects with more than one directional axis. To the best of our knowledge, it would be difficult to use an electrostatic repulsion optimization to solve this problem since such a solution would not contain the necessary information about ordering of the three axes. The presented solution is general and suitable for both axisymmetric and non-axisymmetric encoding objects.An important feature of the presented sampling schemes (15 + 15 + 30 + 30) is that they can be interleaved and be complimentary. This means that any combination of them can be used to define an isotropic sampling scheme with number of samples: (15, 30, 45, 60, 75, 90). Forthcoming studies will investigate which geometries other than the icosahedron and dodecahedron can generate interesting complementary sampling schemes.
Acknowledgements
We acknowledge the following research grants NIH P41EB015902, NIH R01MH074794.References
M. Bak, Mads, N. Nielsen. REPULSION, a novel approach to efficient powder averaging in solid-state NMR. Journal of Magnetic Resonance 125, no. 1 (1997): 132-139.
D. Jones, M. Horsfield, A. Simmons. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 42, no. 3 (1999): 515-525.
N. Shemesh, S. Jespersen, D. Alexander, Y. Cohen, I. Drobnjak, T. Dyrby, J. Finsterbusch, ..., C.F. Westin. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magnetic resonance in medicine 75, no. 1 (2016): 82-87.
E. Caruyer, C. Lenglet, G. Sapiro, R. Deriche. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine, Wiley, 2013, 69 (6):1534-1540.
S. Jespersen, H. Lundell, C. Sønderby, T. Dyrby. Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR in Biomedicine 26, no. 12 (2013): 1647-1662.
C.-F. Westin, H. Knutsson, O. Pasternak, F. Szczepankiewicz, E. Ozarslan, D. van Westen, C. Mattisson, M. Bogren, L. J. O’Donnell, M. Kubicki, D. Topgaard, M. Nilsson. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage 135 (2016): 345– 362.
Figures
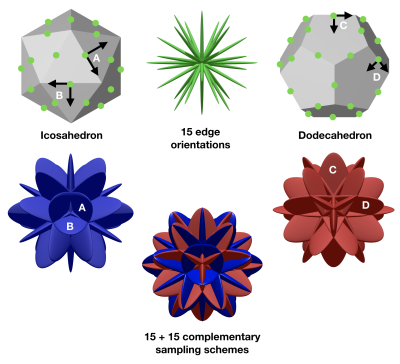
Illustration of isotropic sampling schemes derived from the midpoints of the edges of the icosahedron (top left) and the dodecahedron (top right). Both the icosahedron and the dodecahedron have 30 edges. The midpoints of these edges coincide, but the edges from the two sets are orthogonal. The midpoints are further antipodal, so only 15 directions are defined by these points (middle). The 15 blue coordinate systems/b-tensor, and the 15 red ones are complimentary, and together defines a set of 30 coordinate systems.