Introduction

Intravoxel incoherent motion (IVIM) analysis of the brain has shown to have clinical relevance for the diagnosis of neurological disorders.¹ However, some issues still need to be addressed to make the diffusion parameters more reliable. Especially, physiological variability due to brain pulsation (i.e., bulk motion) as well as pulsatile blood flow during diffusion sensitization leads to artefactual phase dispersion and thus overestimation of the apparent diffusion coefficient.² Recently, a number of groups have reported that second-order motion-compensated (2^nd-MC) diffusion encoding successfully reduced the sensitivity to bulk motion and yielded robust estimation of diffusion parameters in cardiac diffusion-weighted imaging.^3,4 We hypothesized that measurement accuracy of IVIM parameters in the brain can be improved with 2^nd-MC diffusion encoding. Therefore, to obtain more accurate diffusion information, we performed IVIM analysis of the brain with the 2^nd-MC diffusion gradients and compared the diffusion parameters between the 2^nd-MC and conventional diffusion encoding schemes.

Methods

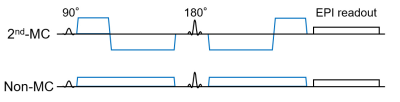
On a 3.0-T MRI, eight healthy volunteers (6 males and 2 females; mean age, 24.8 years; range, 22-34 years) were scanned. Single-shot diffusion echo-planar imaging of the brain was performed with the 2^nd-MC and conventional (non-MC) diffusion gradients (Figure 1). Transverse diffusion-weighted images were obtained with the following imaging parameters: repetition time, 4600 ms; echo time, 143 ms; slice thickness, 6 mm; field of view, 256 mm; imaging matrix, 128 × 128; number of signals averaged, 2; sensitivity encoding factor, 2.1; half-scan factor, 0.7; and b-values, 0, 10, 20, 30, 50, 100, 200, 400, 600, 800, and 1000 s/mm².

Regions of interests (ROIs) were manually drawn in the pons, caudate nucleus, and frontal white matter. Then, mean signal intensities in the ROIs were fitted with the following biexponential function to calculate perfusion-related diffusion coefficient (D*), the fraction (F), and restricted diffusion coefficient (D):

$$$ S = S_{0}\cdot[F\cdot\exp(-bD^{*}) + (1-F)\cdot\exp(-bD)]$$$,

where S and S₀ are signal intensities at a given b-value and without diffusion encoding, respectively. We used a two-step approach to improve the accuracy and robustness of the analysis: D was initially determined using monoexponential function in b-values over 200 s/mm². Then, with the D fixed, D* and F were derived using all b-values. The fitting procedure was performed at MATLAB using the Levenberg-Marquardt nonlinear least-squares algorithm.

Normalized root-mean-square error (nRMSE) was calculated to evaluate the goodness-of-fit of biexponential model for the measured data from each diffusion encoding scheme⁵:

$$$ nRMSE = \frac{\sqrt{RSS/n}}{S_{0} - S_{1000}}$$$,

where RSS is the residual sum of squares and n is the number of measured data. S₀ and S₁₀₀₀ are signal intensities at b-values of 0 and 1000 s/mm², respectively. A smaller nRMSE indicates better fitting quality.

We compared these diffusion parameters and nRMSE between both diffusion encoding schemes using Wilcoxon signed-rank test. A P value of < 0.05 was considered statistically significant.

Results and Discussion

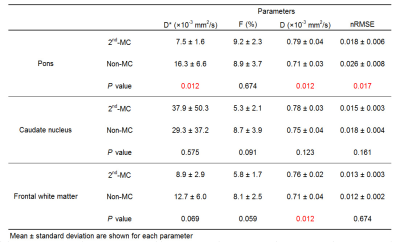
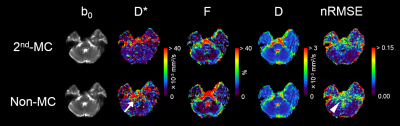
Table 1 shows the diffusion parameters and nRMSE obtained with the 2^nd-MC and non-MC diffusion encoding. Examples of IVIM diffusion parameter and nRMSE maps for one representative subject are shown in Figure 2. The D* of the pons with non-MC was significantly higher than that with 2^nd-MC, whereas there were no significant differences in the D* of the caudate nucleus and frontal white matter between both diffusion encoding schemes. A previous study has demonstrated the largest brain motion in the pons, which is more than 4-fold larger displacement than the frontal lobe.⁶ Thus, our results suggest that D* with non-MC is strongly affected by the bulk motion in the pons. Moreover, the bulk motion-induced signal loss in the pons, especially for low b-values, can be compensated by the 2^nd-MC diffusion encoding, which results in lower D*. In the pons, the nRMSE significantly reduced when using the 2^nd-MC, indicating improved accuracy of the biexponential fitting. We also found significant differences in the D of the pons and frontal white matter between the 2^nd-MC and non-MC. This result might be contributed to the dependence of restricted diffusion on the difference in the diffusion encoding waveform between both schemes.

Conclusion

The 2^nd-MC diffusion encoding scheme reduces the bulk motion effect on IVIM analysis of the brain, thereby improving the measurement accuracy.

Acknowledgements

No acknowledgement found.