4312
Investigating the reproducibility of 4th order Spherical Harmonics dMRI Rotation Invariant Features in White Matter1Athena Project-Team, Inria Sophia Antipolis - Méditerranée, Université Côte d'Azur, Sophia Antipolis - Méditerranée, France
Synopsis
Rotation invariant features can potentially be used as biomarkers for diffusion MRI. One of the most important characteristics of biomarkers is their reproducibility. In the case of diffusion MRI, reproducibility means that if we acquire data from the same subject twice with a short time gap between the two acquisitions we should obtain the same values for the biomarkers. In this work, we investigate the reproducibility of 12 new rotation invariant features that we obtained from 4th order spherical harmonics. Our results suggest that the new invariants are reproducible and can be selected as biomarker-candidates for white matter.
INTRODUCTION
Diffusion MRI (dMRI) is the only imaging technique capable of probing the microstructure of the human brain White Matter (WM) in-vivo. The orientation dependence of the dMRI signal can be a resource - as in the case of tractography - but can also be a hindrance while pursuing the goal of extracting meaningful numerical biomarkers. Several Rotation Invariant Features1 (RIF) have been derived from dMRI in the years to characterize the WM. Recently, we proposed the use of a new set of 12 RIF2,3 extracted from the 4th order Spherical-Harmonics (SH) fitting of the diffusion signal. These new invariants represent a complete set of algebraic independent polynomials which include and extend previously proposed indices such as the power-spectrum invariants. The goal of this work is to investigate the reproducibility of these new invariants in WM taking advantage of the Human Connectome Project4 (HCP) test-retest dataset.METHODS
In order to test our new invariants in-vivo, we selected 44 subjects of the HCP diffusion MRI test-retest dataset for a total of 88 acquisitions. The HCP acquisition protocol is composed of 18 b-value 0 s/mm2 volumes, and three shells at b-values 1000, 2000, and 3000 s/mm2. Each of the three shells is composed of 90 unique gradient orientations. Each image volume is composed of 145 × 174 × 145 voxels with a 1.25 mm isotropic resolution. In this work, we considered three WM ROIs: left hemisphere WM, the Corpus Callosum (CC) and the right hemisphere WM. SH of order 4 are fitted to each shell in order to calculate the 12 RIF following the method presented in Zucchelli et. al. 20183. In order to investigate the reproducibility of our invariants, we extracted the histogram of the values of the invariants in three ROI of the WM, for each of the subjects. For each ROI, we calculated the Kullback-Leibler divergence5 between the 44 subjects of the test dataset versus the 44 subjects of the retest dataset. We defined the reproducibility index for a given invariant as the number of times a test subject shows the lowest divergence for its retest divided by the number of subjects. The baseline reproducibility index - representing the probability that the minimum distance is obtained by chance - is one over the number of subjects, in this case, 1/44 ≈ 0.02.RESULTS
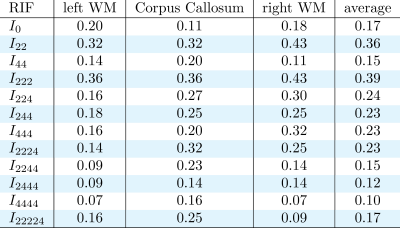
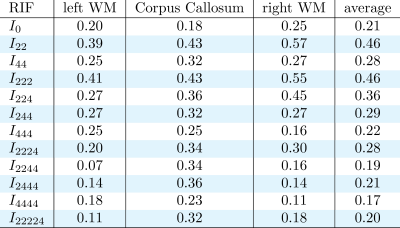
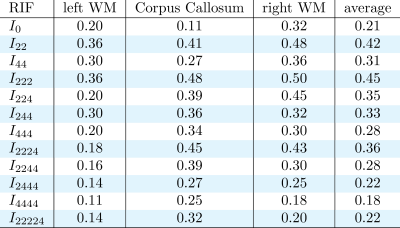
Figure 1 shows some examples of the resulting divergence matrix for two of our new invariants I22 and I222. Ideally, every subject of the test dataset should have the lowest divergence with its own brain in the retest dataset, represented as a dark diagonal in Figure 1. The tables in Figures 2, 3, and 4 show the reproducibility index for all 12 invariants in the three ROIs and their average, for b-value 1000, 2000, and 3000 s/mm2. All the invariants show a reproducibility index at least three times above 0.02 threshold in all the shells. The reproducibility of the invariants is consistent in all the three ROIs with the most reproducible invariants having the highest scores in both the left and right hemisphere WM and the CC. The most reproducible RIFs - with an average reproducibility index above 0.3 - are I22 and I222 for the b-value 1000 s/mm2, I22, I222, and I224 for the b-value 2000 s/mm2, and I22, I44, I222, I224, I244, and I2224 for the b-value 3000 s/mm2. As it is possible to notice the average reproducibility index tends to increase with the b-value. In particular, invariants calculated using 4th order coefficients like I44 or I244 show the sharpest increase in reproducibility. This can be explained by the fact that a high b-value signal presents sharper change in value while changing the gradient orientation. These changes are better captured by high-frequency harmonics.DISCUSSION AND CONCLUSION
Reproducibility is one of the key features of a potential biomarker. In this work, we were able to test the reproducibility of 12 new RIF for dMRI in WM at different b-values. All the new invariants show a reproducibility index at least three times higher than what we expected to obtain by pure chance, with the most reproducible invariant having a reproducibility index more than twenty times higher. Our results suggest that all these new invariants can detect subject-specific WM characteristics to a good degree, with the best performing invariant being able to correctly identify the test-retest pair for almost fifty percent of the subjects. The high reproducibility of the new invariants makes them good candidates for being selected as biomarkers for WM pathologies.Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (ERC Advanced Grant agreement No 694665 : CoBCoM - Computational Brain Connectivity Mapping)
Data were provided by the Human Connectome Project, WU-Minn Consortium(Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657)funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
References
1. Caruyer, E., Verma, R., (2015). "On facilitating the use of hardi in population studies by creating rotation-invariant markers." Medical image analysis 20 (1),87–96.
2. Zucchelli, M., et al. “A Computational Framework For Generating Rotation Invariant Features And Its Application In Diffusion MRI.” Medical Image Analysis, In Press.
3. Zucchelli, M., et al. (2018). “A Closed-Form Solution of Rotation Invariant Spherical Harmonic Features in Diffusion MRI.” MICCAI - Computational Diffusion MRI Workshop 2018, Granada, Spain.
4. Sotiropoulos, S. N., et al. (2013). “Advances in diffusion MRI acquisition and processing in the human connectome project.” Neuroimage 80, 125-143.
5. Kullback, S., Leibler, R. A., (1951). “On information and sufficiency.” Ann. Math. Statist. 22 (1), 79-86.
Figures