Introduction

Multidimensional MRI methods have recently been used in several in vivo investigations, offering a non-invasive characterisation of tissue heterogeneity with an unprecedented level of detail.^1,2 In particular, simultaneous modelling of transverse relaxation- and diffusion-weighted data leads to a more accurate, precise and robust estimation of the model parameters in the case of ill-conditioned estimation problems, such as in the free water elimination (FWE) method.^2,3 In this work, we investigate a dual-echo (DE) Stejskal-Tanner EPI sequence⁴ to acquire diffusion- and T₂-weighted data two times faster than normal. We first validate the sequence using the conventional DTI model with explicit T₂ attenuation and compare it with the case of data acquired using the conventional, individual echo (IE) approach, i.e. one echo per repetition time. The effect of imperfections in the refocusing radiofrequency (RF) pulses is investigated and a simple correction approach is proposed. Finally, we analyse the data from both sequences using the recently introduced FWE with explicit T₂ attenuation model^3,5 (FWET₂).

Methods

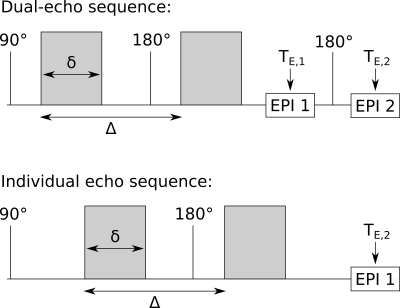
The proposed DE Stejskal-Tanner sequence acquires two spin-echo EPI readouts per repetition time (T_R) (Fig.1). It was implemented on a clinical 3T PRISMA scanner (Siemens Healthineers, Germany). In vivo measurements were performed on 8 healthy volunteers, from whom written informed consent was obtained. The DE experimental protocol included: T_E,1=58ms and T_E,2=100ms; T_R=9s; δ=14ms and Δ=31ms; b-values(directions)=0(9), 0.5(15) and 1.0(30)ms/μm²; matrix-size=96⨉96⨉40; voxel-size=2.5³mm³. An extra IE experiment, echo-time T_E,2=100ms, was acquired for comparison. Due to the equivalence of the first echo from both approaches, the IE dataset comprises the first echo from the DE experiment (T_E,1=58ms) and a second echo individually acquired at T_E,2=100ms (Fig.1).
All diffusion- and T₂-weighted datasets were firstly denoised.⁶ Secondly, corrections of susceptibility- and eddy current-induced distortions were performed using TOPUP and EDDY from FSL.⁷
We analysed the datasets first using the conventional DTI method with explicit, monoexponential T₂ attenuation (DTIT₂), in which the signal is written as: $$S_\mathrm{DTIT_2}(T_\mathrm{E},b,\mathbf{n})=S_0e^{-T_\mathrm{E}/T_2}e^{-b\mathbf{n}^\mathrm{T}\mathbf{D}\mathbf{n}}\;\;\;(1)$$ where $$$S_0$$$, $$$T_2$$$ and $$$\mathbf{D}$$$ are the proton density, the transverse relaxation time and diffusion tensor, respectively; $$$b$$$ and $$$\mathbf{n}$$$ are the diffusion weighting strength and direction. DTIT₂ model parameters, $$$\mathbf{θ}_\mathrm{DTIT_2}=[\mathrm{ln}S_0,D_{11},D_{12},…,D_{33},1/T_2 ]^\mathrm{T}$$$, were estimated by fitting Eq.1 to the experimental datasets, using the weighted-linear least-squares method: $$\mathbf{θ}_\mathrm{DTIT_2}=(\mathbf{X}^\mathrm{T}\mathbf{wX})^{-1}\mathbf{X}^\mathrm{T}\mathbf{wy}\;\;\;(2)$$ where $$$\mathbf{y}$$$ is a column vector whose elements are given by $$$y_i=\mathrm{ln}S_i$$$ and the weighting matrix, $$$\mathbf{w}$$$, is a diagonal matrix whose elements are given by $$$w_{i,i}=S_i^2$$$ ($$$i=1...N$$$, the number of measurements). The i^th row of $$$\mathbf{X}$$$ is written as $$$X_{i,:}=[1,-b_in^2_{ix},-2b_in_{ix}n_{iy},…,-b_{iz}n^2_{iz},-T_{\mathrm{E},i}]$$$.
Secondly, datasets were analysed with the FWET₂ model,^3,5 where the signal is written as: $$S_\mathrm{FWET_2}(T_\mathrm{E},b,\mathbf{n})=S_0[f_we^{-T_\mathrm{E}/T_{2,\mathrm{w}}}e^{-bD_\mathrm{w}}+(1-f_\mathrm{w})e^{-T_\mathrm{E}/T_{2,t}}e^{-b\mathbf{n}^\mathrm{T}\mathbf{D}_\mathrm{t}\mathbf{n}}]\;\;\;(3)$$ $$$T_{2,\mathrm{w}}$$$ and $$$T_{2,\mathrm{t}}$$$ are the free water and tissue transverse relaxation times, respectively, and $$$D_\mathrm{w}$$$ and $$$D_\mathrm{t}$$$ are the diffusion coefficient and tensor for the free water and tissue compartments, respectively. FWET₂ model parameters, $$$\mathbf{θ}_\mathrm{FWET_2}=[S_0,f_\mathrm{w},D_{11},D_{12},…,D_{33},T_{2,\mathrm{t}}]^\mathrm{T}$$$, were estimated using a non-linear least-squares method, with $$$\mathbf{θ}_\mathrm{DTIT_2}$$$ as an initial guess. All models parameters estimations were performed using in-house Matlab scripts. DTI metrics MD and FA were evaluated.⁸ Bulk parameters were estimated at the ventricles and fixed during estimation: $$$T_{2,\mathrm{w}}=0.87\mathrm{s}$$$ and $$$D_\mathrm{w}=3.13\mathrm{μm^2/ms}$$$.
In order to assess imperfections in the refocusing flip-angle, $$$B_1$$$ mapping was performed with 5 IE EPI volumes⁹ having nominal flip-angles: 30°, 60°, 90° and 120°. Other protocol parameters were the same as above.
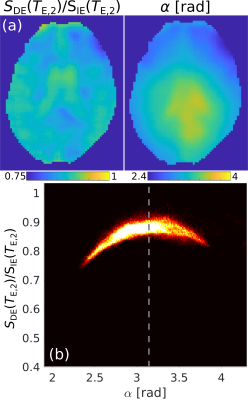
Finally, the lower signal amplitude of the second echo of the DE sequence, $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$, caused by imperfections in the refocusing RF pulses, was corrected by estimating the slope versus the corresponding signal of the IE sequence, $$$S_\mathrm{IE}(T_{\mathrm{E},2})$$$ (Fig.2b). We refer to this dataset as the DE corrected (DEC).

Results

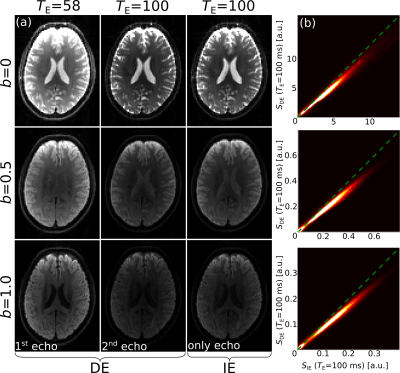
Fig.2 shows the diffusion- and T₂-weighted images from the DE and the IE sequences. The joint histograms on the right-hand side indicate a lower signal amplitude in the 2^nd echo of the DE sequence, $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$, versus the only echo of the IE sequence, $$$S_\mathrm{IE}(T_{\mathrm{E},2})$$$. The slope of the plot of $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$ vs. $$$S_\mathrm{IE}(T_{\mathrm{E},2})$$$, averaged over the eight subjects, was: 0.878±0.007.
Fig.3 demonstrates that the reduced signal amplitude of $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$ with respect to $$$S_\mathrm{IE}(T_{\mathrm{E},2})$$$ is tightly correlated with the imperfections in the refocusing flip-angle.
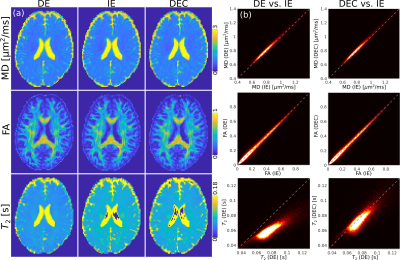
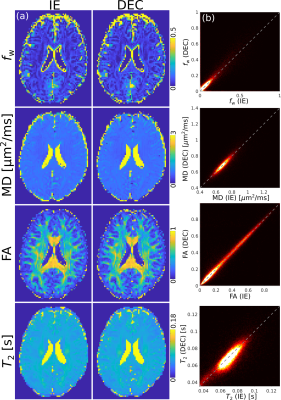
Fig.4 depicts the DTIT₂ maps for the DE, IE and DEC data. We observe that DTI maps are not affected by the reduced signal amplitude of the second echo, whereas the values in T₂ for the DE sequence are underestimated, compared to the IE sequence. The DEC data provide DTIT₂ parameters more similar to the IE case.
Fig.5 demonstrates the application of the DEC approach for the assessment of FWET₂ parameters.

Discussion and conclusions

The acquisition of a dual-echo Stejskal-Tanner sequence reduced the acquisition time by a factor of two in the presented diffusion- and T₂-weighted experiments, for the case in which 2 echoes are required. Imperfections in the refocusing flip-angle lead to a reduction of the signal amplitude of the second echo in the DE sequence, $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$, compared to the IE signal, $$$S_\mathrm{IE}(T_{\mathrm{E},2})$$$ (Fig.3).¹⁰ We demonstrated that the signal reduction factor is stable over subjects and used this factor to correct $$$S_\mathrm{DE}(T_{\mathrm{E},2})$$$. The DTIT₂ maps calculated from the DEC data are very similar to the standard IE (Fig.4). Finally, we analysed the experimental data using the FWET₂ model, showing that there is a high correlation between model parameters from IE data and DEC data.

Acknowledgements

We thank Mrs Claire Rick for proof reading the manuscript.