4262

Rapid parametric optimization of transmit coil arrays: a proof-of-concept
Jose EC Serralles1, Elfar Adalsteinsson1, Lawrence L Wald2, and Luca Daniel1
1Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States

Synopsis

In this paper we efficiently combine a coil optimization process with an electromagnetic field solver and show preliminary proof of concept on simple systems leading to 22% to 45% improvement in Signal to Noise Ratios.

Introduction

The performance (e.g. Signal to Noise Ratio) of Magnetic Resonance parallel transmit systems (ptx) can be greatly improved by optimal adjustment of coil parameters. Current procedures include either (1) manually adjusting fabricated coils, (2) or manually adjusting coils in a commercial simulator environment and re-executing complete simulations each time (3) or using an automatic optimization process but still executing complete simulations at each time.[1][2][3][4] All such approaches can lead to prohibitive times, specially when attempted on large ptx systems. In this work we intrinsically combine the optimization process with a recently developed solver that does not require a complete simulation at each step of the optimization, and show preliminary proof of concept on simple systems.

Materials

We employ the voxelized Billy head model of the Virtual Family, which provides the distribution of electrical properties for simulation.[5] We design the coil using gmsh, an open--source meshing tool for 2D and 3D geometries.[6] For the electromagnetic simulation, we use MARIE, a coupled integral equation electromagnetic field solver.[7] We developed our coil optimization process using MATLAB.[8]

Methods

We pre-compute once the Magnetic Resonance Green's Function (MRGF) for the voxelized Billy head model at $$$B_0$$$ of 7T or operating frequency of 297.2MHz.[5] We then re-use it at each step of our optimization for an extremely efficient solution of the fields generated by different coil configurations corresponding to different parameter values, $$$\mu$$$. The optimization is set to maximize the signal--to--noise ratio (SNR) of the system, i.e.
$$ \underset{\mu}{\text{max}} \frac{S}{P} $$
where
$$S=\sum_{v\in\text{ROI}}\left|H_v^+\right|^2$$
and
$$P=\sum_{v\in V} \sigma_v \left|E_v\right|^2\Delta V\text{.}$$
$$$H^+$$$ denotes the right-handed component of the magnetic field; $\sigma$ denotes the electric conductivity; $$$E$$$ denotes the electric field; and $\Delta V$ denotes the volume of each voxel. The decision variables that we consider are the radius of each loop and its distance from the origin.
We achieve tuning and matching by attaching capacitors to distributed ports along each loop and constraining them to be
$$C=\text{argmin}_C \|S\|_{\rm F}^2\text{ s.t. }C_l \leq C_i \leq C_u, \; i = 1, \ldots, N_c$$
where $$$S$$$ is the scattering parameter matrix and the norm is the Frobenius norm. The scattering parameter matrix is given by $$$S = \left(Z_p+z_0I\right)^{-1}\left(Z_p-z_0I\right)$$$ where $$$Z_p$$$ is the impedance parameter matrix. We shim by maximizing the SNR over the excitation applied to each coil while ensuring unit magnitude or smaller:
$$\alpha = \text{argmax}_\alpha \frac{S}{P}\text{ s.t. }|\alpha_i|^2 \leq 1, \; i = 1, \ldots, N_p$$

Simulation Results

In our first simulation, we maximized the SNR specifically on a small region of interest (ROI) corresponding to the location of the hypothalamus. We used a single loop coil, and allow the optimizer to adjust both its radius and its distance from the origin. We started with an arbitrarily chosen radius of 6 cm and distance of 15 cm, yielding an SNR of 79. After 10 iterations (i.e. 20 minutes), we converged to an SNR of 115, with radius 15.9 cm and distance 12.0 cm. The final radius is the specified upper bound that was given to the optimizer.
In our second simulation, we maximized the SNR on hypothalamus region. We used two loops, adjusting independently radii and distances of each loop. We started with 6 cm radii and 15 cm distances, yielding an SNR of 121. After merely 4 iterations (i.e. 85 minutes), we converged to an SNR of 148, with radii 13.9 cm and 15.8 cm and with distances 18.0 cm and 18.4 cm, respectively.

Discussion & Conclusion

In our first experiment, our optimizer increased the SNR 45% by increasing the radius and moving the coil closer to the body. Intuitively, this result is logical because a larger and closer loop typically produces larger magnetic fields. In our second experiment, our optimizer increased the SNR by a factor of 22%. Interestingly, both loops were moved farther away from the head and were made large.

Acknowledgements

This work was supported by NIH Grant 2R01EB006847-09A1.

References

  1. Zhang, Xiaoliang, Kamil Ugurbil, and Wei Chen. "Microstrip RF surface coil design for extremely high‐field MRI and spectroscopy." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 46, no. 3 (2001): 443-450.
  2. Ohliger, Michael A., and Daniel K. Sodickson. "An introduction to coil array design for parallel MRI." NMR in Biomedicine: An International Journal Devoted to the Development and Application of Magnetic Resonance In vivo 19, no. 3 (2006): 300-315.
  3. Liu, Wentao, Donglin Zu, Xin Tang, and Hua Guo. "Target-field method for MRI biplanar gradient coil design." Journal of Physics D: Applied Physics 40, no. 15 (2007): 4418.
  4. Cobos Sanchez, Clemente, Salvador Gonzalez Garcia, Luis Diaz Angulo, Carlos Moreno De Jong Van Coevorden, and Amelia Rubio Bretones. "A divergence-free BEM method to model quasi-static currents: Application to MRI coil design." Progress in Electromagnetics Research 20 (2010): 187-203.
  5. Christ A, Kainz W, Hahn E G, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B, Schmitt P, Hollenbach H P, Shen J, Oberle M, Szczerba D, Kam A, Guag J W, and Kuster N, The Virtual Family - development of surface-based anatomical models of two adults and two children for dosimetric simulations, Physics in Medicine and Biology, 55(2):N23-N38, 2010.
  6. C. Geuzaine and J.-F. Remacle. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering 79(11), pp. 1309-1331, 2009
  7. Villena, Jorge Fernández, Athanasios G. Polimeridis, Yigitcan Eryaman, Elfar Adalsteinsson, Lawrence L. Wald, Jacob K. White, and Luca Daniel. "Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods." IEEE Transactions on Biomedical Engineering 63, no. 11 (2016): 2250-2261.
  8. MATLAB. version 9.4.0 (R2018a). Natick, Massachusetts: The MathWorks Inc.; 2018.

Figures

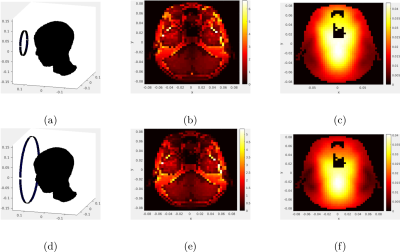
First simulation experiment involving optimization of one loop's radius and distance from the origin. Top row depicts the (a) initial coil design in front of the head, (b) the initial electric field along a transverse slice, and (c) the initial magnetic field along the same transverse slice. Bottom row depicts the (d) final coil design, (e) the final electric field along a transverse slice, and (f) the final magnetic field along a transverse slice.

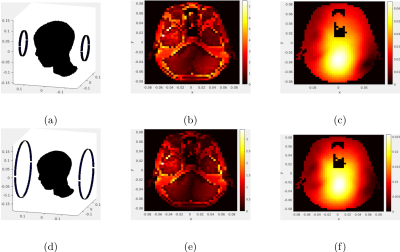
Second simulation experiment involving optimization of two loops' radii and distances from the origin. Top row depicts the (a) initial coil design around the head, (b) the initial electric field along a transverse slice, and (c) the initial magnetic field along the same transverse slice. Bottom row depicts the (d) final coil design, (e) the final electric field along a transverse slice, and (f) the final magnetic field along a transverse slice.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
4262