Introduction

Parallel transmission (PTx) via RF transmit arrays is a key technology in high field MRI, offering several degrees of freedom in RF control for improving contrast uniformity and reducing local SAR.^1,2 Local SAR, however, depends substantially on the subject’s anatomy, particularly morphological aspects such as tissue distribution and positioning within the RF coil.^3,4 To ensure compliance to RF safety limits these variations can lead to large conservative safety margins derived from population-based statistics, which compromise PTx utilization.

Various research efforts have aimed to leverage the imaging capabilities of MRI in order to establish subject-specific anatomical models from MR image data.^3,5 The bottleneck in utilizing such information in a local SAR estimate, however, is the time-consuming computation of the resulting RF fields. This problem will continue to grow with increasing channel count and field strength.

Recently, a new approach was shown which computes SAR as a function of anatomical differences with respect to a reference model rather than solving for the entire anatomy itself.⁶ In the current work we improve the scalability of this approach by presenting a reduced order model based on this framework, building on approaches for modelling dielectric perturbations external to the body.⁷

Methods

Setup
The numerical approach is guided by a 7T neuroimaging setup, consisting of a resonant high-pass single-channel quadrature birdcage as well as a resonant 8-channel TEM transmit array simulated using xFDTD at -40 dB convergence (v7.4, Remcom, State College, PA). Custom post-processing routines were implemented in Matlab (r2016a, Mathworks inc., MA, USA) on a system equipped with parallel computing on 12 CPU cores and two GPU cards (K40, Nvidia, Santa Clara, USA).

The heterogeneous model “Duke” from the Virtual Family⁸ was assigned as the background model, and anatomical perturbations were synthesized by scaling and translating this model up to 5% in size and up to 1.5 cm in each direction, respectively. The accuracy of the obtained field solution was evaluated in terms of 10g-averaged SAR.

Model Order Reduction
The equations describing the RF field in the human body can be cast in terms of equivalent scattering currents, where the total current in the actual subject is decomposed into a pre-computed background current and a perturbation current, which is solved for as follows

$$$J=J^b+χG_bJ=(I-χG_b)^{-1}J^b$$$ Eq. 1

where $$$J_b = χE_b$$$ denotes the background current which is derived from the background electric field $$$E_b$$$, $$$χ=ε-ε_b$$$ denotes the difference in electric susceptibility between the actual subject and the background model. $$$G_b$$$ denotes the background dyadic Green’s tensor which accounts for the response of the database model.

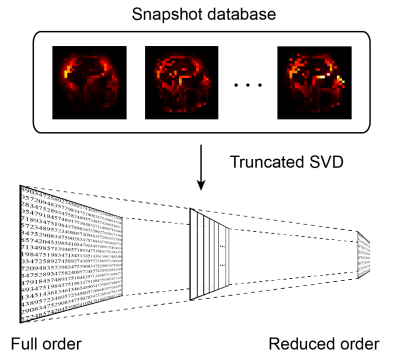
A series of 25000 randomized model perturbations was evaluated using a custom solver and the resulting perturbation currents were stored to form a so-called ‘snapshot’ database. From this, a reduced basis $$$U_r$$$ was extracted via a truncated SVD, which is used to to rewrite Eq. 1 in reduced form as

$$$J=U_r(I_r-U^H_rχG_bU_r)^{-1}U^H_rJ^b .$$$ Eq. 2

This procedure is graphically illustrated in Fig. 1. The truncation level $$$r$$$ can be chosen to control the trade-off between speed and accuracy. The reduced order model permits either iterative or direct inversion of Eq. 2, which can be advantageous when solving for multiple PTx channels simultaneously. Furthermore, when different coils are evaluated, only the background current term needs to be updated as the perturbation term can be decoupled from the coil.

Results

Construction of the snapshot database and reduced model required ~24 hours on the GPU-accelerated computational server. The convergence of the reduced order model with respect to truncation level r is evaluated in Fig. 2 for the quadrature birdcage. At a truncation level of 20000, the model yielded an order-of-magnitude compression in terms of the number of unknowns, and two orders-of-magnitude in terms of memory requirement of the final system matrix compared to the full order model. Compared to the conventional FDTD solver, we reached a speed-up of almost a factor of five in terms of CPU time.


Results obtained in the TEM-array driven in the first three circular polarized modes are shown in Fig. 3 showing similar performance as obtained in the birdcage. Furthermore, in this case we can exploit a direct inverse to solve the reduced system of Eq. 2, yielding an order of magnitude speed-up compared to FDTD.

Discussion and Conclusion

An efficient approach to local SAR prediction is proposed based on model order reduction, which substantially reduces the memory footprint and computation time with respect to a conventional method. By employing a direct inverse we can solve for multiple transmit channels simultaneously, which significantly improves the scalability in view of upcoming high field systems with an increasing number of RF transmit channels. Additionally, a prediction of the B₁ field is available at the minor cost of a matrix-vector product, which may replace the time-intensive B₁ calibration scan required for PTx pulse calculation.

An advantage of the proposed approach is that the reduced model can be recycled when applied to different RF coils, at the minor cost of one simulation to construct the background field. Finally, further improvements of the accuracy and speed can be realized by considering multiple reference models, which will naturally provide a better starting point and improve the compression performance.

Acknowledgements

This work was supported by the Netherlands Organization for Scientific Research (NWO) through a VENI fellowship (TTW.16820).