4234
An automatic design method for arbitrary shaped shielded gradients using a singular value decomposition and meta-heuristic method
Kazuya Sakaguchi1 and Yasuhiko Terada1
1Institute of Applied Physics, University of Tsukuba, Tsukuba, Japan
1Institute of Applied Physics, University of Tsukuba, Tsukuba, Japan
Synopsis
Most of gradients coils are cylindrical or planar, but deformed gradients that fit an object shape should have superior performance. A truncated singular value decomposition (SVD) is a design method for arbitrary shaped gradients, but the design process is time-consuming, especially for shielded gradients. Moreover, coil performance, such as coil inductance and power dissipation cannot be optimized. In this study, we proposed a new strategy that combines the SVD method with a meta-heuristic method for automatically optimizing desired performance for shielded gradients.
INTRODUCTION
Gradients coils with arbitrary geometries are promising because the coil performance can be optimized to suit an object shape. They are often designed by a combination of matrix inversion optimization techniques and discrete representations of current surface, which is solved using a truncated singular value decomposition (SVD) [1,2]. However, the selection method of the SVD eigenmodes is empirical, and hence the gradient performances, such as coil inductance and power dissipation, cannot be optimized. Moreover, design for shielded gradients using the SVD requires time and effort, because there is a trade-off between pattern complexity and field accuracy, and hence main and shield coils should be alternatively calculated with many iterations [3]. To address these issues, we proposed a method for designing shielded gradients with optimized performance to be desired. The proposed method combines the SVD method with a meta-heuristic approach. We designed a shielded gradients with power efficiency optimization, and demonstrated that the proposed method outperformed the original SVD method without meta- heuristic approach.DESIGN METHODS
In our previous study, we used the similar method to optimize given performance for an unshielded coil [4]. Here, we added the following improvements to the previous algorithm: (1) We modified the genetic algorithm to an artificial bee colony algorithm (ABC) to improve the computational efficiency, and (2) added a constraint of the maximum leakage field.Figure 1 shows a flowchart of the proposed method. In the SVD module, the current potential T that generated the target magnetic field B was calculated back by the SVD calculation for each of main and shield coils. The current surface was represented by triangular meshes, and the current distribution was obtained from the contour lines of the current potential Ti of each node i. The required magnetic field was expressed by Bj = ∑iATi at each evaluation point j, where A was calculated from the Biosavart’s law. By calculating the inverse matrix of A with SVD, T was expressed as the sum of orthonormal basis Tk(mode). After determining the number of truncation modes k, the alternative SVD calculations of the main and shield coils were repeated twice to correct the error caused by the mutual interference of the magnetic fields, which gave an initial solution.
In the ABC optimization module, Tk was multiplied by the weight coefficient ck and redefined as T = ∑kckTk, and a combination of ck that formed optimal coil was automatically searched by the ABC algorithm. The optimization was performed to maximize an objective function formulated according to the target performance. In this study, only the main coil was optimized to simplify the calculation.
The SVD-ABC method was tested for a cylindrical shielded gradient coils. In order to verify the superiority of this method, we compared two methods: the SVD method alone and the SVD-ABC module method. Fig. 2 shows the geometric conditions of the designed coil. The main coil (truncation number = 20, number of windings = 36) and shield coil (k = 392, number of windings = 16) were arranged coaxially. The diameter of each conductor was 0.5 mm. The gradient magnetic field was formed in a 26 mm sphere, and the shield area was a cylindrical surface coaxial with the main coil.
In the ABC algorithm, the objective function was set as follows to optimize the power efficiency (population = 50, generation = 1200, and employ bee rate = 0.5),
$$f=\frac {\eta^2}{RN^2\max{(|B_{leak}|)}}$$.
Here, $$$\eta$$$ was the gradient field efficiency, $$$R$$$ was the resistance, $$$N$$$ was the number of windings, and $$$\max{(|B_{leak}|)}$$$ was the maximum strength of the leakage magnetic field on the shield surface. We set a limiting condition that the nonlinearity of the gradient field and the leakage field strength were 10 % and 10 µT or less.
Figure of merit (FOM) was defined as $$$\eta^2/R\sqrt \delta$$$ [4], where $$$\delta$$$ was the RMS error of the gradient magnetic field. The power efficiency was calculated as $$$P = \eta^2/R$$$.
RESULT AND DISCUSSION
Fig. 3 shows the winding pattern of the designed shielded gradient coil. Table 1 summarizes the coil performance. The SVD-ABC yielded a coil with a higher current density at the center of the winding pattern because the curve was steeper there. As a result, the efficiency of the gradient field in the center was improved (Table 1), the overall resistance was reduced, and the power efficiency was improved by 35%, while maintaining the maximum leakage within the given constraint. This indicates that the automatic optimization by the ABC algorithm worked effectively.CONCLUSION
We proposed a new design method for arbitrarily shaped shielded gradient coils. We demonstrated that the combination the SVD method with the ABC algorithm enables the automatic design of shielded gradient coils optimized for the desired performance.Acknowledgements
No acknowledgement found.References
[1] M. Abe et al., Phys. Plasmas, 10 (2003) 1022 -1033. [2] M. Abe, IEEE Trans. Magn., 49 (2013) 5645 -5655. [3] M. Ave et al., IEEE Trans. Magn., 50(2015) 5100911. [4] K. Matsuzawa, ISMRM 4336 (2017).Figures
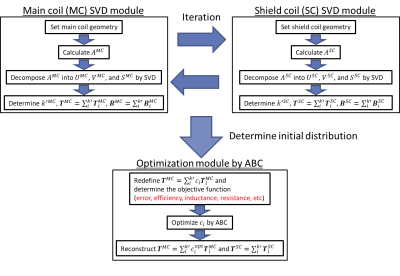
Fig1.
Flowchart of the SVD-ABC method
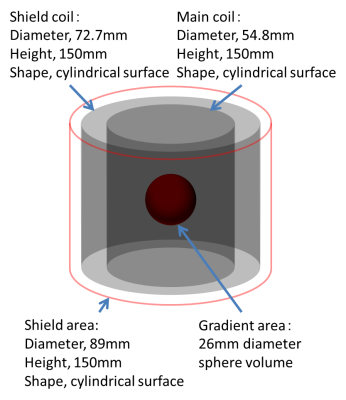
Fig2.
Geometric conditions of test shielded gradient coils design
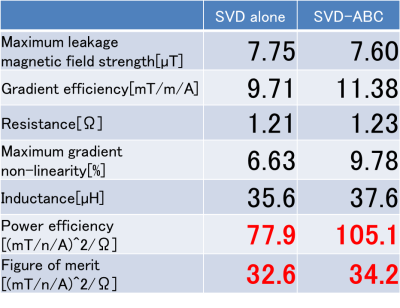
Table1.
Performance of designed shielded gradient coils
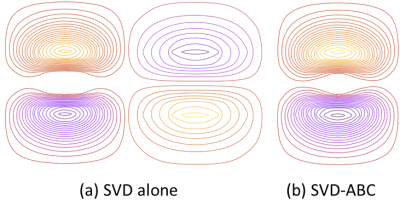
Fig.3: Designed coil
winding pattern. (a) Designed with the SVD alone. (b) Designed with the SVD-ABC.
The shield coil in (b) was the same as that in (a) and was not shown.